
Try the SAT Math Test Module 1st with Real Exam Questions and Simple Detailed Solutions
How much have you learned so far? Are you progressing by taking the SAT Tests and also learning all Math problems by understanding solutions. This is the 6th Math test. Like the other exams, it has the same format and all the necessary features for you to become a master in math. You just take the SAT Test Module First to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after step-by-step explanations.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each split into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 1st.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 1ST
The first module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 1st are from easy to difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 1st. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH TEST ANSWERS WITH EXPLANATION AND TIPS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: What is 10% of 470?
A) 37
B) 47
C) 423
D) 460
Choice B is correct. 10% of a quantity means 10/100 times the quantity. Therefore, 10% of 470 can be represented as 10/100 (470), which is equivalent to 0.10(470), or 47. Therefore, 10% of 470 is 47.
Choice A is incorrect. This is 10% of 370, not 10% of 470.
Choice C is incorrect. This is 90% of 470, not 10% of 470.
Choice D is incorrect. This is 470 – 10, not 10% of 470.
It is a simple percentage calculation, it is best to practice using the Desmos calculator.
470 divided by 10%
470 x 10/100
4700/100
47 Answer.
2nd Question
4x + 6 = 18
Question: Which equation has the same solution as the given equation?
A) 4x = 108
B) 4x = 24
C) 4x = 12
D) 4x = 3
Choice C is correct. Subtracting 6 from both sides of the given equation yields 4x =12, which is the equation given in choice C. Since this equation is equivalent to the given equation, it has the same solution as the given equation.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
It is also a simple one.
4x + 6 = 18 (When one thing moves from one side to another, it changes its sign from ‘negative to positive’ or ‘positive to negative.’)
4x = 18 – 6
4x = 12 (Option C: We found our answer but what if we were asked to find the value of x.)
Then, 4x = 12
x = 12/4
x = 3.
3rd Question
Question: If y = 5x + 10, what is the value of y when x = 8?
A) 23
B) -23
C) -50
D) 50
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 50. Substituting 8 for x in the given equation yields y = 5(8) + 10, or y = 50. Therefore, the value of y is 50 when x = 8.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
y = 5x + 10
Put the value of x which is 8. (x = 8)
y = 5(8) + 10
y = 40 + 10
y = 50.
4th Question
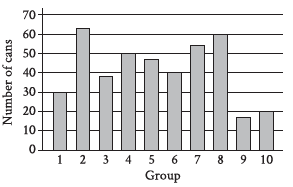
Question: The bar graph shows the distribution of 419 cans collected by 10 different groups for a food drive. How many cans were collected by group 6?
A) 40
B) 267
C) 266
D) 6
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Option A is the correct answer. The correct answer is 40. The height of each bar in the bar graph shown represents the number of cans collected by the group specified at the bottom of the bar. The bar for group 6 reaches a height of 40. Therefore, group 6 collected 40 cans.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
The question only asks for Group 6, not 1 to 6 or so. So the bar graph shows, a horizontal line, and there is the number 6 (Group 6). On vertically, you will see the bar goes to the line of 40 (Number of Cans).
5th Question
Question: The table gives the distribution of votes for a new school mascot and grade level for 80 students.

Choice C is correct. If one of these students is selected at random, the probability of selecting a student whose vote for the new mascot was for a lion is given by the number of votes for a lion divided by the total number of votes. The given table indicates that the number of votes for a lion is 20 votes, and the total number of votes is 80 votes. The table gives the distribution of votes for 80 students, and the table shows a total of 80 votes were counted. It follows that each of the 80 students voted exactly once. Thus, the probability of selecting a student whose vote for the new mascot was for a lion is 20/80, or 1/4
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
In order to answer correctly, we understand the question and the table. The question asks to find the probability of getting the lion out of the total number of students.
We know from the table the total number of students is: 80
The students who vote for the lion are: 9 + 2 + 9 = 20
The formula of probability is:
Number of favorable outcomes 20
______________________________________________ = _______
Total number of possible outcomes 80
= 20/80
= 1/4.
Final Answer: C) 1/4.
6th Question
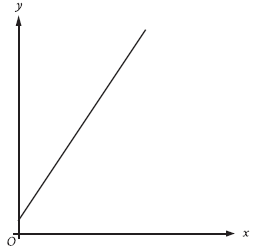
Question: The graph represents the total charge, in dollars, by an electrician for x hours of work. The electrician charges a one-time fee plus an hourly rate. What is the best interpretation of the slope of the graph?
A) The electrician’s hourly rate
B) The electrician’s one-time fee
C) The maximum amount that the electrician charges
D) The total amount that the electrician charges
Choice A is correct. It’s given that the electrician charges a one-time fee plus an hourly rate. It’s also given that the graph represents the total charge, in dollars, for x hours of work. This graph shows a linear relationship in the xy-plane. Thus, the total charge y, in dollars, for x hours of work can be represented as y = mx + b, where m is the slope and (0, b) is the y-intercept of the graph of the equation in the xy-plane. Since the given graph represents the total charge, in dollars, by an electrician for x hours of work, it follows that its slope is m, or the electrician’s hourly rate.
Choice B is incorrect. The electrician’s one-time fee is represented by the y-coordinate of the y-intercept, not the slope, of the graph.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
First, let’s understand the question, the graph only has a slope but no data. It is an option-based question, which means, our answer is hidden in options. We need to find what the slope of the graph represents.
Let’s apply the options:
Note: We must understand one thing that a slope means both x and y sides are increasing.
A) The electrician’s hourly rate:
It is the most accurate option, cause an hourly rate means both the hour and price are increasing.
B) The electrician’s one-time fee:
A one-time fee can’t grow and become a slope.
C) The maximum amount that the electrician charges:
Again, it is a growing slope from both sides, not one side.
D) The total amount that the electrician charges:
It is also not possible.
7th Question
Question: Square X has a side length of 12 centimeters. The perimeter of square Y is 2 times the perimeter of square X. What is the length, in centimeters, of one side of square Y?
A) 6
B) 10
C) 14
D) 24
Choice D is correct. The perimeter, P, of a square can be found using the formula P = 4s, where s is the length of each side of the square. It’s given that square X has a side length of 12 centimeters. Substituting 12 for s in the formula for the perimeter of a square yields P = 4(12), or P = 48. Therefore, the perimeter of square X is 48 centimeters. It’s also given that the perimeter of square Y is 2 times the perimeter of square X. Therefore, the perimeter of square Y is 2(48), or 96, centimeters. Substituting 96 for P in the formula P = 4s gives 96 = 4s. Dividing both sides of this equation by 4 gives 24 = s. Therefore, the length of one side of square Y is 24 centimeters.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem:
Square X has a side length of 12 cm. The perimeter of square Y is 2 times the perimeter of square X. What is the length, in centimeters, of one side of square Y?
Step-by-Step Solution:
Step 1: Understand the relationship between the side length and perimeter of a square
The perimeter of a square is given by the formula:
Perimeter = 4 × side length.
Step 2: Calculate the perimeter of square X
For square X, the side length is 12 cm. Using the formula:
Perimeter of square X = 4 × 12 = 48 cm.
Step 3: Relate the perimeter of square Y to square X
We are told that the perimeter of square Y is 2 times the perimeter of square X:
Perimeter of square Y = 2 × 48 = 96 cm.
Step 4: Determine the side length of the square Y
Using the perimeter formula for a square, solve for the side length of square Y:
Perimeter of square Y = 4 × side length of square Y.
Substitute the known perimeter of square Y (96 cm):
96 = 4 × side length of square Y.
Divide both sides by 4:
The side length of square Y = 96/4 = 24 cm.
Verification:
1. Calculate the perimeter of square Y using the side length of 24 cm:
4 × 24 = 96 cm.
This matches the given condition that square Y’s perimeter is 2 times that of square X.
2. The solution is consistent with the problem conditions.
Final Answer: The side length of square Y is 24 centimeters.
8th Question
Question: An object is kicked from a platform. The equation h represents this situation, where h = -4.9t2 + 7t + 9 is the height of the object above the ground, in meters, t seconds after it is kicked. Which number represents the height, in meters, from which the object was kicked?
A) 0
B) 4.9
C) 7
D) 9
Choice D is correct. It’s given that the equation h = -4.9t2 + 7t + 9 represents this situation, where h is the height, in meters, of the object t seconds after it is kicked. It follows that the height, in meters, from which the object was kicked is the value of h when t = 0. Substituting 0 for t in the equation h = -4.9t2 + 7t + 9 yields h = -4.9(0)2 + 7(0) + 9, or h = 9. Therefore, the object was kicked from a height of 9 meters.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem:
The height h of an object kicked from a platform is modeled by the equation:
h = −4.9t2 + 7t + 9,
where h is the height above the ground (in meters), and t is the time (in seconds) after the object is kicked.
We are asked to find the height from which the object was kicked.
Step-by-Step Solution:
Step 1: Understand the question
The height from which the object was kicked refers to the initial height of the object above the ground at t = 0 (the moment it is kicked). This is the starting height, which can be found by substituting t = 0 into the equation for h.
Step 2: Substitute t = 0 into the equation
The given equation is:
h = −4.9t2 + 7t + 9.
Substitute t = 0:
h = −4.9(0)2 + 7(0) + 9.
Step 3: Simplify the equation
Simplify each term:
h = −4.9(0) + 7(0) + 9.
h = 0 + 0 + 9.
h = 9.
Step 4: Interpret the result
At t = 0, the height of the object is 9 meters. This means the object was kicked from a platform 9 meters above the ground.
Verification:
1. At t = 0, only the constant term +9 in the equation contributes to the height. This is because the terms −4.9t2 and 7t both equal zero when t = 0.
2. The constant term in a quadratic height equation like this always represents the initial height (starting height).
Final Answer: The height from which the object was kicked is 9 meters.
9th Question
f(x) = 4x2 − 50x + 126
Question: The given equation defines the function f. For what value of x does f(x) reach its minimum?
A) 6.25
B) 16
C) 6.5
D) 16.25
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
The correct answer is Option A.

Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Recognize the nature of the function
The given function is a quadratic function of the form:
f(x) = ax2 + bx + c,
where:
~ a = 4,
~ b = −50,
~ c = 126.
Since the coefficient of x2(a = 4) is positive, the parabola opens upwards, meaning the vertex represents the minimum value of the function.

Verification of the Solution
To verify, substitute x = 6.25 into the equation f(x) to confirm that it represents the minimum:
1. Compute f(6.25):
f(6.25) = 4(6.25)2 − 50(6.25) + 126.
2. Simplify (6.25)2:
(6.25)2 = 39.0625.
3. Substitute back:
f(6.25) = 4(39.0625) − 50(6.25) + 126.
f(6.25) = 156.25 − 312.5 + 126.
f(6.25) = −30.25.
Thus, the minimum value of the function is −30.25 at x = 6.25. This confirms our calculation.
Final Answer: A) 6.25.
10th Question
Question: Vivian bought party hats and cupcakes for $71. Each package of party hats costs $3, and each cupcake costs $1. If Vivian bought 10 packages of party hats, how many cupcakes did she buy?
A) 4
B) 96
C) 20
D) 41
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 41. The number of cupcakes Vivian bought can be found by first finding the amount Vivian spent on cupcakes. The amount Vivian spent on cupcakes can be found by subtracting the amount Vivian spent on party hats from the total amount Vivian spent. The amount Vivian spent on party hats can be found by multiplying the cost per package of party hats by the number of packages of party hats, which yields $3 . 10, or $30. Subtracting the amount Vivian spent on party hats, $30, from the total amount Vivian spent, $71, yields $71 – $30, or $41. Since the amount Vivian spent on cupcakes was $41 and each cupcake cost $1, it follows that Vivian bought 41 cupcakes.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
We are tasked with determining how many cupcakes Vivian bought. Let’s solve this step by step and verify the solution.
Step-by-Step Solution
Step 1: Define the variables
~ Let the number of cupcakes Vivian bought be x.
~ The cost of each package of party hats is 3.
~ The cost of each cupcake is 1.
Step 2: Write an equation for the total cost
Vivian spent $71 total, and she bought 10 packages of party hats. Therefore, the total cost can be expressed as:
3(10) + 1(x) = 71.
Step 3: Simplify the equation
Simplify the terms:
30 + x = 71.
Step 4: Solve for x
Subtract 30 from both sides:
x = 71 − 30.
x = 41.
Thus, Vivian bought 41 cupcakes.
Verification
To verify, calculate the total cost:
1. The cost of 10 packages of party hats:
10 × 3 = 30.
2. The cost of 41 cupcakes:
41 × 1 = 41.
3. Total cost:
30 + 41 = 71.
This matches the given total cost of $71. The solution is correct.
Final Answer: D) 41.
11th Question
z2 + 10z – 24 = 0
Question: What is one of the solutions to the given equation?
A) 2 or -12
B) 4 or -24
C) -2 or 12
D) -4 or 24
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is either 2 or -12. The left-hand side of the given equation can be rewritten by factoring. The two values that multiply to -24 and add to 10 are 12 and -2. It follows that the given equation can be rewritten as (z + 12)(z – 2) = 0. Setting each factor equal to 0 yields two equations: z +12 = 0 and z – 2 = 0. Subtracting 12 from both sides of the equation z + 12 = 0 results in z = -12. Adding 2 to both sides of the equation z – 2 = 0 results in z = 2. Note that 2 and -12 are examples of ways to enter a correct answer.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
There are two ways to do this equation.
1. Quadratic Method
2. Factorize Method
I will show you both methods and tell you when can you use them.
To identify, an equation should look like this: ax2 + bx + c = 0
Notice, the question looks the same: z2 + 10z – 24 = 0
Let’s use the Quadratic Method:
Step-by-Step Solution:
Step 1: Identify the quadratic equation structure.
The given equation is in the standard form:
az2 + bz + c = 0
Here:
~ a = 1 (coefficient of z2),
~ b = 10 (coefficient of zzz),
~ c = −24 (constant term).
Step 2: Solve using the quadratic formula.

( + ) This sign means that it can be positive or negative, so let’s try both ways.

Final Answer: A) 2 or -12.
Let’s use the Factorize Method:
Step-by-Step Solution:
Step 1: Identify the equation structure (ax2 + bx + c = 0).
The given quadratic equation is:
z2 + 10z − 24 = 0
Here, the goal is to factorize it into the form:
(z + p)(z + q) = 0
where p and q are numbers such that:
1. Their product is c = −24.
2. Their sum is b = 10.
Step 2: Find two numbers that satisfy the conditions.
We need two numbers whose:
~ Product = −24,
~ Sum = 10.
By trial or inspection:
p = 12 and q = −2
because:
12 ⋅ (−2) = −24 (c comes by multiplying two numbers)
12 + (−2) = 10 (b comes by adding the same two numbers)
It must be the same numbers you multiply or add and it should give c and b. If it doesn’t happen then it is not a factor and you cannot solve the equation using this method.
Step 3: Write the equation in factored form.
Using p = 12 and q = −2, the quadratic equation becomes:
z2 + 10z − 24 = (z + 12)(z − 2) = 0
Step 4: Solve for z.
Set each factor equal to 0:
1. z + 12 = 0
z = −12
2. z − 2 = 0
z = 2
Thus, the two solutions are:
z = −12 and z = 2
Step 5: Verify the solutions.
Substitute both z = 2 and z = −12 back into the original equation z2 + 10z − 24 = 0:
1. For z = 2:
(2)2 + 10(2) − 24 = 4 + 20 − 24 = 0
2. For z = −12:
(−12)2 + 10(−12) − 24 = 144 − 120 − 24 = 0
Both solutions are correct.
Final Answer: The two solutions are z = 2 and z = −12.
12th Question
Question: Bacteria are growing in a liquid growth medium. There were 300,000 cells per milliliter during an initial observation. The number of cells per milliliter doubles every 3 hours. How many cells per milliliter will there be 15 hours after the initial observation?
A) 1,500,000
B) 2,400,000
C) 4,500,000
D) 9,600,000
Choice D is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
We are tasked with calculating the number of bacteria cells per milliliter after 15 hours, given:
1. Initially, there are 300,000 cells per milliliter.
2. The number of cells doubles every 3 hours.
Step-by-Step Solution:
Step 1: Understand the growth pattern
The problem states that the number of cells doubles every 3 hours. This is an example of exponential growth, where the amount of growth depends on a doubling factor for a given time.
The formula for this type of growth is:
N(t) = N0 ⋅ 2t/T,
where:
~ N(t) = the number of cells after t hours,
~ N0 = the initial number of cells (300,000),
~ T = the doubling time (3 hours),
~ t = total time elapsed (15 hours in this case).
Step 2: Substitute the known values into the formula
We are solving for N(15):
N(15) = 300,000 ⋅ 215/3.
Here:
~ N0 = 300,000,
~ T = 3,
~ t = 15.
Step 3: Simplify the exponent
The exponent is:
15/3 = 5.
Thus:
N(15) = 300,000 ⋅ 25.
Step 4: Calculate 25
25 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32.
Substituting this value:
N(15) = 300,000 ⋅ 32.
Step 5: Perform the multiplication
300,000 ⋅ 32 = 9,600,000.
Verification:
Let’s confirm step-by-step:
1. Doubling every 3 hours means the cells will double 15/3 = 5 times.
2. The initial count is 300,000. Doubling it 5 times results in:
~ After 3 hours: 300,000 ⋅ 2 = 600,000,
~ After 6 hours: 600,000 ⋅ 2 = 1,200,000,
~ After 9 hours: 1,200,000 ⋅ 2 = 2,400,000,
~ After 12 hours: 2,400,000 ⋅ 2 = 4,800,000,
~ After 15 hours: 4,800,000 ⋅ 2 = 9,600,000,
The calculation matches the formula-based answer.
Final Answer:
After 15 hours, the number of cells per milliliter will be: 9,600,000.
13th Question
Question: The product of two positive integers is 546. If the first integer is 11 greater than twice the second integer, what is the smaller of the two integers?
A) 21
B) 28
C) 32
D) 35
Choice A is correct. The x-intercept of a graph in the xy-plane is the point on the graph where y = 0. It’s given that function h is defined by h(x) = 4x + 28. Therefore, the equation representing the graph of y = h(x) is y = 4x + 28. Substituting 0 for y in the equation y = 4x + 28 yields 0 = 4x + 28. Subtracting 28 from both sides of this equation yields -28 = 4x. Dividing both sides of this equation by 4 yields -7 = x. Therefore, the x-intercept of the graph of y = h(x) in the xy-plane is (-7, 0). It’s given that the x-intercept of the graph of y = h(x) is (a, 0). Therefore, a = -7. The y-intercept of a graph in the xy-plane is the point on the graph where x = 0. Substituting 0 for x in the equation y = 4x + 28 yields y = 4(0) + 28, or y = 28. Therefore, the y-intercept of the graph of y = h(x) in the xy-plane is (0, 28). It’s given that the y-intercept of the graph of y = h(x) is (0, b). Therefore, b = 28. If a = -7 and b = 28, then the value of a + b is -7 + 28, or 21.
Choice B is incorrect. This is the value of b, not a + b.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the value of –a + b, not a + b.
Problem Breakdown:
We are tasked with finding the value of a + b, where:
~ a is the x-intercept of the graph of y = h(x).
~ b is the y-intercept of the graph of y = h(x). The function is defined as h(x) = 4x + 28.
Step-by-Step Solution:
Step 1: Find the x-intercept (a)
The x-intercept occurs when y = 0. Substituting h(x) = 0 into the function:
0 = 4x + 28.
Solve for x:
4x = −28,
x = −7.
Thus, the x-intercept is a = −7.
Step 2: Find the y-intercept (b)
The y-intercept occurs when x = 0. Substituting x = 0 into the function:
h(0) = 4(0) + 28.
Simplify: h(0) = 28.
Thus, the y-intercept is b = 28.
Step 3: Find a + b
Substitute the values of a and b into a + b:
a + b = −7 + 28.
Simplify: a + b = 21.
Verification:
~ For x-intercept:
Substituting y = 0 in 4x + 28 = 0, we found x = −7.
~ For y-intercept:
Substituting x = 0 in 4x + 28, we found y = 28.
~ a + b = −7 + 28 = 21.
Both intercepts and the result are consistent.
Final Answer: The value of a + b is: 21.
14th Question
Question: One of the factors of 2x3 + 42x2 + 208x is x + b, where b is a positive constant. What is the smallest possible value of b?
A) 8
B) 13
C) -8
D) -13
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 8. Since each term of the given expression, 2x3 + 42x2 + 208x, has a factor of 2x, the expression can be rewritten as 2x(x2) + 2x(21x) + 2x(104), or 2x(x2 + 21x + 104). Since the values 8 and 13 have a sum of 21 and a product of 104, the expression x2 + 21x + 104 can be factored as (x + 8)(x + 13). Therefore, the given expression can be factored as 2x(x + 8)(x + 13). It follows that the factors of the given expression are 2, x, x + 8, and x + 13. Of these factors, only x + 8 and x + 13 are of the form x + b, where b is a positive constant. Therefore, the possible values of b are 8 and 13. Thus, the smallest possible value of b is 8.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
There are two methods to solve this equation.
1. Quadratic Formula
2. Factoring Formula
1. Let’s use the Quadratic Formula:
Step-by-Step Solution:
Step 1: Factor out the greatest common factor (GCF)
Start by factoring out the GCF of the terms in the polynomial:
2x3 + 42x2 + 208x = 2x(x2 + 21x + 104).
Thus, the polynomial simplifies to:
2x(x2 + 21x + 104).
Now, we focus on the quadratic x2 + 21x + 104 to find the factor x + b.
Step 2: Use the Factor Theorem
The Factor Theorem states that if x + b is a factor of x2 + 21x + 104, then substituting x = −b into the polynomial should yield 0:
f(x) = x2 + 21x + 104, and f(−b) = 0.
Substitute x = −b into x2 + 21x + 104:
(−b)2 + 21(−b) + 104 = 0.
Simplify: b2 − 21b + 104 = 0.
Step 3: Solve for b
To solve the quadratic b2 − 21b + 104 = 0, we use the quadratic formula:
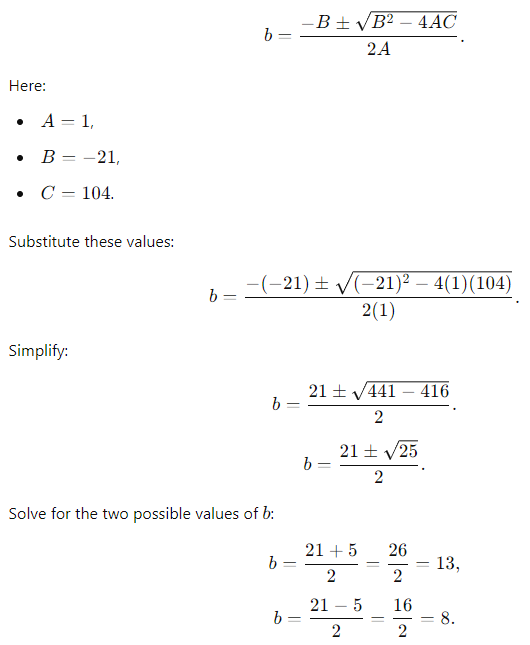
Thus, the two possible values of b are 13 and 8.
Step 4: Identify the smallest positive b
The smallest positive value of b is:
b = 8.
Verification:
To verify, substitute x = −8 into x2 + 21x + 104 to confirm that x + 8 is indeed a factor:
f(−8) = (−8)2 + 21(−8) + 104.
f(−8) = 64 − 168 + 104 = 0.
This confirms that x + 8 is a factor of the polynomial.
Final Answer: The smallest possible value of b is: 8.
2. Let’s use the Factoring Formula:
Step 1: Factor out the greatest common factor (GCF)
The GCF of 2x3, 42x2, and 208x is 2x.
2x3 + 42x2 + 208x = 2x(x2 + 21x + 104)
Step 2: Factor the quadratic x2 + 21x + 104
Now, we focus on factoring x2 + 21x + 104.
We need two numbers that multiply to 104 (the constant term) and add to 21 (the coefficient of x):
~ The two numbers are 13 and 8, because 13 × 8 = 104 and 13 + 8 = 21.
So, we can factor x2 + 21x + 104 as:
x2 + 21x + 104 = (x + 13)(x + 8)
Step 3: Combine the factors
The fully factored form of the expression is:
2x3 + 42x2 + 208x = 2x(x + 13)(x + 8)
Step 4: Determine the smallest possible value of b
The factors include x + 13 and x + 8. Here, b represents the positive constant from x + b.
From the factors, b = 8 is the smallest possible value.
Verification
To verify, substitute b = 8 into x + b:
x + 8
This is indeed a factor of the original expression, as shown by the factorization.
Final Answer: The smallest possible value of b is: 8.
15th Question
y = −1.5
y = x2 + 8x + a
Question: In the given system of equations, a is a positive constant. The system has exactly one distinct real solution. What is the value of a?
A) 29
B) 14.5
C) 58.5
D) -29
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is the correct option. The correct answer is 29/2. According to the first equation in the given system, the value of y is -1.5. Substituting -1.5 for y in the second equation in the given system yields -1.5 = x2 + 8x + a. Adding 1.5 to both sides of this equation yields 0 = x2 + 8x + a + 1.5. If the given system has exactly one distinct real solution, it follows that 0 = x2 + 8x + a + 1.5 has exactly one distinct real solution. A quadratic equation in the form 0 = px2 + qx + r, where p, q, and r are constants, has exactly one distinct real solution if and only if the discriminant, q2 – 4pr, is equal to 0. The equation 0 = x2 + 8x + a + 1.5 is in this form, where p = 1, q = 8, and r = a + 1.5. Therefore, the discriminant of the equation 0 = x2 + 8x + a + 1.5 is (8)2 – 4(1)(a + 1.5), or 58 – 4a. Setting the discriminant equal to 0 to solve for a yields 58 – 4a = 0. Adding 4a to both sides of this equation yields 58 = 4a. Dividing both sides of this equation by 4 yields 58/4 = a, or 29/2 = a. Therefore, if the given system of equations has exactly one distinct real solution, the value of a is 29/2. Note that 29/2 and 14.5 are examples of ways to enter a correct answer.
Choice A is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
Step 1: Set the equations equal to each other
Since both equations equal y, we set them equal to each other:
−1.5 = x2 + 8x + a
Rearrange to form a standard quadratic equation:
x2 + 8x + a + 1.5 = 0
x2 + 8x + (a + 1.5) = 0
Step 2: Conditions for one distinct real solution
A quadratic equation has exactly one distinct real solution when its discriminant is zero. The discriminant (Δ) of a quadratic equation ax2 + bx + c = 0 is given by:
Δ = b2 − 4ac
Here:
a = 1 (coefficient of x2),
b = 8 (coefficient of x),
c = a + 1.5 (constant term).
Substitute into the discriminant formula:
Δ = 82 − 4(1)(a + 1.5)
Δ = 64 − 4(a + 1.5)
Step 3: Set the discriminant equal to zero
For the quadratic to have exactly one distinct real solution:
64 − 4(a + 1.5) = 0
Simplify: 64 − 4a − 6 = 0
58 = 4a
a = 58/4
a = 14.5
Step 4: Verify the solution
Substitute a = 14.5 into the quadratic equation:
x2 + 8x + (14.5 + 1.5) = 0
x2 + 8x + 16 = 0
Find the discriminant:
Δ = 82 − 4(1)(16)
Δ = 64 − 64
Δ = 0
Since the discriminant is zero, the equation has exactly one distinct real solution. This confirms a = 14.5 is correct.
Final Answer: B) 14.5.
16th Question
f(x) = (x + 6)(x + 5)(x − 4)
Question: The function f is given. Which table of values represents y = f(x) − 3?
Option A)
| x | y |
|---|---|
| -6 | -9 |
| -5 | -8 |
| 4 | 1 |
Option B)
| x | y |
|---|---|
| -6 | -3 |
| -5 | -3 |
| 4 | -3 |
Option C)
| x | y |
|---|---|
| -6 | -3 |
| -5 | -2 |
| 4 | 7 |
Option D)
| x | y |
|---|---|
| -6 | 3 |
| -5 | 3 |
| 4 | 3 |
Choice B is correct. It’s given that f(x) = (x + 6)(x + 5)(x – 4) and y = f(x) – 3. Substituting (x + 6)(x + 5)(x – 4) for f(x) in the equation y = f(x) – 3 yields y = (x + 6)(x + 5)(x – 4) – 3. Substituting -6 for x in this equation yields y = (-6 + 6)(-6 + 5)(-6 – 4) – 3, or y = – 3. Substituting -5 for x in the equation y = (x + 6)(x + 5)(x – 4) – 3 yields y = (-5 + 6)(-5 + 5)(-5 – 4) – 3, or y = – 3. Substituting 4 for x in the equation y = (x + 6)(x + 5)(x – 4) – 3 yields y = (4 + 6)(4 + 5)(4 – 4) – 3, or y = – 3. Therefore, when x = -6 then y = -3, when x = -5 then y = -3, and when x = 4 then y = -3. Thus, the table of values in choice B represents y = f(x) – 3.
Choice A is incorrect. This table represents y = x – 3 rather than y = f(x) – 3.
Choice C is incorrect. This table represents y = x + 3 rather than y = f(x) – 3.
Choice D is incorrect. This table represents y = f(x) + 3 rather than y = f(x) – 3.
Problem:
Given the function:
f(x) = (x + 6)(x + 5)(x − 4)
Determine which table of values represents the function:
y = f(x) − 3
Step-by-Step Solution:
Step 1: Understand the Given Functions
1. Original Function:
f(x) = (x + 6)(x + 5)(x − 4)
This is a cubic function with roots at x = −6, x = −5, and x = 4.
2. Modified Function:
y = f(x) − 3
This transformation shifts the graph of f(x) downward by 3 units. For every x, the new y-value is 3 less than the original f(x)-value.
Step 2: Identify Key Points to Populate the Table
To construct a table of values for y = f(x) − 3, we need to evaluate y at specific x-values. Typically, these x-values are chosen based on the roots and other significant points of the original function.
Key x-values to consider:
~ Roots of f(x): x = −6, x = −5, x = 4
~ Additional Points: Choose other x-values if needed for completeness
Step 3: Calculate y for Each Key x-value
1. For x = −6:
f(−6) = (−6 + 6)(−6 + 5)(−6 − 4)
f(-6) = (0)(−1)(−10)
f(-6) = 0 x -1 x -10
f(-6) = 0
So, the value of f(-6) is equal to 0.
y = f(−6) − 3
y = 0 − 3
y = −3
2. For x = −5:
f(−5) = (−5 + 6)(−5 + 5)(−5 − 4)
f(-5) = (1)(0)(−9)
f(-5) = 1 x 0 x -9
f(-5) = 0
So, the value of f(-5) is equal to 0.
y = f(−5) − 3
y = 0 − 3
y = −3
3. For x = 4:
f(4) = (4 + 6)(4 + 5)(4 − 4)
f(4) = (10)(9)(0)
f(4) = 10 x 9 x 0
f(4) = 0
So, f(4) is equal to 0.
y = f(4) − 3
y = 0 − 3
y = −3
Hence, if:
x = -6 then y is -3.
x = -5 then y is -3.
x = 4 then y is -3.
| x | y |
|---|---|
| -6 | -3 |
| -5 | -3 |
| 4 | -3 |
Final Answer: Option B.
17th Question
Question: The regular price of a shirt at a store is $11.70. The sale price of the shirt is 80% less than the regular price, and the sale price is 30% greater than the store’s cost for the shirt. What was the store’s cost, in dollars, for the shirt?
A) 1.7
B) 1.3
C) 1.8
D) 2.3
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice C is the correct option. The correct answer is 1.8. It’s given that the regular price of a shirt at a store is $11.70, and the sale price of the shirt is 80% less than the regular price. It follows that the sale price of the shirt is $11.70(1 – 80/100), or $11.70(1 – 0.8), which is equivalent to $2.34. It’s also given that the sale price of the shirt is 30% greater than the store’s cost for the shirt. Let x represent the store’s cost for the shirt. It follows that 2.34 = (1 + 30/100)x, or 2.34 = 1.3x. Dividing both sides of this equation by 1.3 yields x = 1.80. Therefore, the store’s cost, in dollars, for the shirt is 1.80. Note that 1.8 and 9/5 are examples of ways to enter a correct answer.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis:
We are tasked with finding the store’s cost for a shirt when the following conditions are provided:
1. The regular price of the shirt is $11.70.
2. The sale price of the shirt is 80% less than the regular price.
3. The sale price is 30% greater than the store’s cost for the shirt.
We need to calculate the store’s cost.
Step-by-Step Solution:
Step 1: Calculate the Sale Price of the Shirt
The sale price is 80% less than the regular price. This means we subtract 80% of the regular price from the regular price:
Sale Price = Regular Price − 0.8 ⋅ Regular Price
Substitute Regular Price = 11.70:
Sale Price = 11.70 − 0.8 ⋅ 11.70
First, calculate 0.8 ⋅ 11.70
0.8 ⋅ 11.70 = 9.36
Now subtract:
Sale Price = 11.70 − 9.36 = 2.34
The sale price is $2.34.
Step 2: Relate the Sale Price to the Store’s Cost
The sale price is 30% greater than the store’s cost. Let the store’s cost be C. The sale price is given by:
Sale Price = C + 0.3 ⋅ C
Factor C from the right-hand side:
Sale Price = 1.3 ⋅ C
Substitute Sale Price = 2.34
2.34 = 1.3 ⋅ C
Step 3: Solve for the Store’s Cost
To find C, divide both sides of the equation by 1.3:
C = 2.34/1.3
Perform the division: C = 1.8
The store’s cost is $1.80.
Verification:
1. Check the Sale Price: If the store’s cost is $1.80, then the sale price (30% greater than the cost) is:
Sale Price = 1.3 ⋅ 1.80 = 2.34
This matches the given sale price, so the cost calculation is correct.
2. Check the Regular Price Reduction: The sale price of $2.34 is indeed 80% less than the regular price of $11.70:
80% of Regular Price = 0.8 ⋅ 11.70 = 9.36
Regular Price – 80% Reduction = 11.70 – 9.36 = 2.34
This confirms the correctness of the sale price.
Final Answer: The store’s cost for the shirt is: 1.80.
18th Question
Question: A certain town has an area of 4.36 square miles. What is the area, in square yards, of this town? (1 mile = 1,760 yards)
A) 404
B) 7,674
C) 710,459
D) 13,505,536
Choice D is correct. Since the number of yards in 1 mile is 1,760, the number of square yards in 1 square mile is (1,760)(1,760) = 3,097,600. Therefore, if the area of the town is 4.36 square miles, it is 4.36(3,097,600) = 13,505,536, in square yards.
Choice A is incorrect and may result from dividing the number of yards in a mile by the square mileage of the town.
Choice B is incorrect and may result from multiplying the number of yards in a mile by the square mileage of the town.
Choice C is incorrect and may result from dividing the number of square yards in a square mile by the square mileage of the town.
Problem Analysis:
We need to convert the given area of the town from square miles to square yards. The given information is:
~ Area of the town: 4.36 square miles
~ Conversion factor: 1 mile = 1,760 yards.
We know that to convert square miles to square yards, we need to square the conversion factor for miles to yards.
Step-by-Step Solution:
Step 1: Conversion Factor from Miles to Yards
The given conversion is:
1 mile = 1,760 yards.
To convert square miles to square yards, square the conversion factor:(1 mile)2 = (1,760 yards)2.
Perform the squaring:
1 square mile = 1,760 × 1,760 = 3,097,600 square yards.
Step 2: Convert 4.36 Square Miles to Square Yards
We are given the area of the town as 4.36 square miles. Multiply this by the conversion factor:
Area in square yards = 4.36 × 3,097,600.
Perform the multiplication:
4.36 × 3,097,600 = 13,505,536 square yards.
Verification:
Recompute the multiplication step for accuracy:
~ Multiply 4.36 by 3,097,600:
4.36 × 3,097,600 = 13,505,536.
The computation is correct.
Final Answer: The area of the town is: 13,505,536 square yards.
19th Question
| x | y |
|---|---|
| 18 | 130 |
| 23 | 160 |
| 26 | 178 |
Question: For line h, the table shows three values of x and their corresponding values of y. Line k is the result of translating line h down 5 units in the xy-plane. What is the x-intercept of line k?
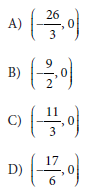
Choice D is the correct answer.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Find the equation of line h

Step 2: Find the y-intercept (b) of line h
We substitute m = 6 and one point, such as (18, 130), into y = mx + b:
130 = 6(18) + b.
Simplify:
130 = 108 + b.
Solve for b:
b = 130 − 108
b = 22.
The equation of line h is:
y = 6x + 22.
Step 3: Equation of line k
Line k is obtained by translating line h down 5 units. This means we subtract 5 from the y-values:
y = 6x + 22 − 5
y = 6x + 17.
The equation of line k is:
y = 6x + 17.
Step 4: Find the x-intercept of line k
The x-intercept occurs when y = 0. Set y = 0 in the equation of line k:
0 = 6x + 17.
Solve for x:
6x = −17.
x = −17/6.
The x-intercept is: (−17/6, 0).
Verification:
The slope m = 6 and y-intercept translation were computed correctly. Substituting values confirms that x = −17/6 satisfies the equation.
Final Answer: D) (−17/6, 0).
20th Question
Question: In the xy-plane, the graph of the equation y = −x2 + 9x − 100 intersects the line y = c at exactly one point. What is the value of c?
A) − 481/4
B) −100
C) − 319/4
D) − 9/2
Choice C is correct. In the xy-plane, the graph of the line y = c is a horizontal line that crosses the y-axis at y = c and the graph of the quadratic equation y = –x2 + 9x – 100 is a parabola. A parabola can intersect a horizontal line at exactly one point only at its vertex. Therefore, the value of c should be equal to the y-coordinate of the vertex of the graph of the given equation. For a quadratic equation in vertex form, y = a(x – h)2 + k, the vertex of its graph in the xy-plane is (h, k). The given quadratic equation, y = –x2 + 9x – 100, can be rewritten as
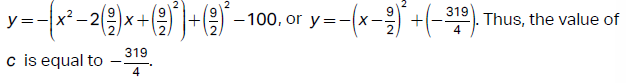
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis:
We are tasked with finding the value of c such that the graph of the quadratic equation y = −x2 + 9x − 100 intersects the horizontal line y = c at exactly one point. This condition implies that the quadratic equation has exactly one solution, meaning the discriminant (Δ) of the quadratic equation must be 0.
Step-by-Step Solution:
Step 1: Set the two equations equal to each other
The line y = c intersects the parabola y = −x2 + 9x − 100 when:
−x2 + 9x − 100 = c.
Rearrange the equation to form a standard quadratic equation:
−x2 + 9x − 100 − c = 0.
Simplify:
−x2 + 9x + (−100 − c) = 0.
This equation can also be written as:
x2 − 9x + (100 + c) = 0 (after multiplying through by -1).
Step 2: Apply the discriminant condition
For a quadratic equation of the form ax2 + bx + c = 0, the discriminant is given by:
Δ = b2 − 4ac.
Here, the coefficients are:
a = 1,
b = −9, and
c = 100 + c.
The quadratic equation has exactly one solution when Δ = 0. Set the discriminant equal to 0:
Δ = (−9)2 − 4(1)(100 + c) = 0.
Simplify: 81 − 4(100 + c) = 0.
Step 3: Solve for c
Distribute: 81 − 400 − 4c = 0.
Simplify: −319 − 4c = 0.
Solve for c:
4c = −319.
c = −319/4.
Final Answer: C) −319/4.
Verification:
Substitute c = −319/4 into the quadratic equation x2 − 9x + (100 + c) = 0. The discriminant calculation will confirm that Δ = 0, verifying that the parabola intersects the line at exactly one point.
Final Answer: C) −319/4.
21th Question
2x + 3y = 7
10x + 15y = 35
Question: For each real number r, which of the following points lies on the graph of each equation in the xy-plane for the given system?
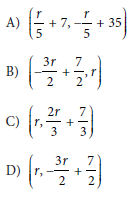
Choice B is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
It is an option-based question, which means without implying, the given equation of the question, into the options, you cannot find the correct one.
Step 1: The System of Equations
The system of equations is:
2x + 3y = 7
10x + 15y = 35
The second equation is a multiple of the first [10x + 15y = 5(2x + 3y)], so we only need to check which option satisfies 2x + 3y = 7. You can choose the first or second equation from above, it doesn’t matter but we are against the time so let’s pick that saves time, equation first.
Step 2: Substituting Each Option into 2x + 3y = 7

Let’s use the same substitute for Options C and D, even though we have our correct option, we can still solve the complete question for better preparation.

6. we have got -5r + 21 = 14 of Option D: Solve for r
-5r = 14 – 21
-5r = -7 (we can cut the minus sign from both sides.)
r = 7/5.
Now, we have the r value from all 4 Options. Let’s put them in the given equation: 2x + 3y = 7 (If you use this equation to solve the question then r = 7. Whichever option gives you r = 7 is the correct option. But if you use the second equation 10x + 15y = 35, then r = 35.)
The correct option is Option B.
-3r + 7 + 3r
-3r + 3r + 7 (Both 3r cut one another)
7.
Final Answer: Option B.
22th Question
Question:

A) 104
B) 624
C) 180
D) 60
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 104. An equilateral triangle is a triangle in which all three sides have the same length and all three angles have a measure of 60o. The height of the triangle, k root of 3, is the length of the altitude from one vertex. The altitude divides the equilateral triangle into two congruent 30-60-90 right triangles, where the altitude is the side across from the 60o angle in each 30-60-90 right triangle. Since the altitude has a length of k root of 3, it follows from the properties of 30-60-90 right triangles that the side across from each 30o angle has a length of k and each hypotenuse has a length of 2k. In this case, the hypotenuse of each 30-60-90 right triangle is a side of the equilateral triangle; therefore, each side length of the equilateral triangle is 2k. The perimeter of a triangle is the sum of the lengths of each side. It’s given that the perimeter of the
equilateral triangle is 624; therefore, 2k + 2k + 2k = 624, or 6k = 624. Dividing both sides of this equation by 6 yields k =104.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Learn to use the Desmos calculator, so this question will become easy for you. Let’s start!

Final Answer: The value of k is: 4.
Did you try all the features and get comfortable using them? You should work on using the calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must try to work on your speed and spend less time on the beginning and more on the later questions. This is the 6th Practice Test of SAT Math Module 1st.
Either you can take the 7th Practice Test of SAT Math or the 6th Practice Test of SAT Math Module 2nd.
- SAT Test 6th (Math Module 2nd)
- SAT Test 7th (Math Module 1st)
- SAT Test 6th (Reading and Writing Module 1st)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


