
Prepare For The SATs: Math Test Module 2nd with Simple Explanations, Tips and Tricks
Have you taken the 1st Test? If yes, then you are in the right place. This is the 2nd Test of Module 2nd. We have designed a similar exam format with all the necessary features for you to become a master in Math. You take the SAT Test Module Second to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 2nd.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 2ND
The second module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 2nd are only difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 2nd. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH STUDY GUIDE AND PROBLEM SOLUTIONS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: What is 20% of 440?
A) 44
B) 88
C) 880
D) 1,760
Choice B is correct. 20% of 440 can be calculated as (20/100)(440), which is equivalent to, 8800/100, or 88.
Choice A is incorrect. This is 10%, not 20%, of 440.
Choice C is incorrect. This is 200%, not 20%, of 440.
Choice D is incorrect. This is 400%, not 20%, of 440.
You should learn to use the Desmos Calculator. It will make your calculation easy.
2nd Question
Question:
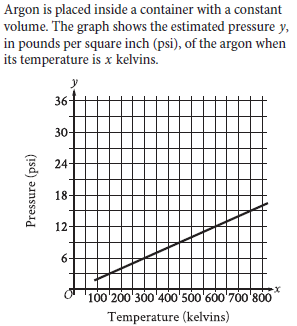
What is the estimated pressure of the argon, in psi, when the temperature is 600 kelvins?
A) 6
B) 12
C) 300
D) 600
Choice B is correct. For the graph shown, the x-axis represents temperature, in kelvins, and the y-axis represents the estimated pressure, in pounds per square inch (psi). The estimated pressure of the argon when the temperature is 600 kelvins can be found by locating the point on the graph where the value of x is equal to 600. The graph passes through the point (600, 12). This means that when the temperature is 600 kelvins, the estimated pressure is 12 psi.
Choice A is incorrect. This is the estimated pressure, in psi, of the argon when the temperature is 300 kelvins, not 600 kelvins.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the temperature, in kelvins, of the argon.
Step 1: Understand the linear relationship
From the graph, we know the pressure y increases linearly with temperature x, meaning the relationship between them is proportional. The general equation is:
y = mx + b
where:
~ m is the slope of the line,
~ b is the y-intercept (pressure when x = 0).
Step 2: Identify points from the graph
The given point is:
~ At x = 600, y = 12.
We need another point to calculate the slope. From the graph, another point we can use is:
~ At x = 0, y = 0.
Step 3: Calculate the slope
The slope m is calculated as:
m = Δy/Δx
m = y2 – y1 / x2 – x1
Using the points (x1, y1) = (0, 0) and (x2, y2) = (600, 12):
m = 12 – 0 / 600 – 0
m = 12/600
m = 0.02.
Step 4: Write the linear equation
Substitute m = 0.02 and b = 0 into the linear equation y = mx + b
y = 0.02x
Step 5: Verify the equation at x = 600
Substituting x = 600 into y = 0.02x:
y = 0.02 × 600 = 12
This confirms the equation is correct.
Step 6: Interpretation
The linear equation y = 0.02x correctly models the relationship between the temperature (x) in kelvins and the pressure (y) in psi, given the adjusted condition where the pressure is 12 psi, 600K.
Final Answer:
Using this corrected model, the pressure when the temperature is 600K is indeed: 12 psi.
3rd Question
Question: The function f is defined by f(x) = 4x − 3. What is the value of f(10)?
A) -30
B) 37
C) 40
D) 43
Choice B is correct. It’s given that the function f is defined by f(x) = 4x – 3. Substituting 10 for x in the given function yields f(10) = 4(10) – 3, which is equivalent to f(10) = 40 – 3, or f(10) = 37. Therefore, the value of f(10) is 37.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect. This is the value of f(10) for the function f(x) = 4x, not f(x) = 4x – 3.
Choice D is incorrect. This is the value of f(10) for the function f(x) = 4x + 3, not f(x) = 4x – 3.
Step 1: Understand the problem
The problem asks us to determine the value of the function f(x) = 4x − 3 when x = 10. This involves function evaluation, which means substituting the given input x = 10 into the function formula and simplifying it.
Step 2: Substitute x = 10 into f(x)
We are given:
f(x) = 4x − 3
Substitute x = 10 into the equation:
f(10) = 4(10) − 3
Step 3: Simplify the expression
1) Calculate 4(10):
4(10) = 40
2) Subtract 3:
40 − 3 = 37
Thus, the value of f(10) is:
f(10) = 37
Step 4: Verification
To confirm, let’s recheck:
~ The formula is f(x) = 4x − 3.
~ Substituting x = 10:
f(10) = 4(10) − 3
f(10) = 40 − 3
f(10) = 37
The calculation is correct.
Final Answer: B) 37.
4th Question
Question: Which expression is equivalent to 16x3y2 + 14xy?
A) 2xy(8xy + 7)
B) 2xy(8x2y + 7)
C) 14xy(2x2y + 1)
D) 14xy(8x2y + 1)
Choice B is correct. Since 2xy is a common factor of each term in the given expression, the expression can be rewritten as 2xy(8x2y + 7).
Choice A is incorrect. This expression is equivalent to 16x2y2 + 14xy.
Choice C is incorrect. This expression is equivalent to 28x3y2 + 14xy.
Choice D is incorrect. This expression is equivalent to 112x3y2 + 14xy.
Step 1: Understand the problem
We are tasked with factoring the expression 16x3y2 + 14xy. Factoring involves finding the greatest common factor (GCF) of the terms and expressing the expression in a simpler factored form. Then, we compare the results with the provided options.
Step 2: Identify the GCF
The two terms in the expression are:
1) 16x3y2
2) 14xy
Step 2.1: Determine the GCF of the coefficients 16 and 14: The greatest common factor of 16 and 14 is 2.
Step 2.2: Determine the GCF of the variables x3 and x: The smallest power of x is x, so the GCF for x is x.
Step 2.3: Determine the GCF of the variables y2 and y: The smallest power of y is y, so the GCF for y is y.
Thus, the GCF of 16x3y2 + 14xy is: 2xy
Step 3: Factor out the GCF
Now, divide each term in 16x3y2 + 14xy by 2xy:
1) For 16x3y2:
16x3y2 divided by 2xy = 8x2y
2) For 14xy:
14xy divided by 2xy = 7
After factoring out 2xy, the expression becomes:
2xy(8x2y + 7)
Step 4: Verify with the options
From the factored form 2xy(8x2y + 7), compare it to the given options:
Option A: 2xy(8xy + 7) — Incorrect (does not match 8x2y + 7).
Option B: 2xy(8x2y + 7) — Correct (matches the factored form).
Option C: 14xy(2x2y + 1) — Incorrect (incorrect factorization).
Option D: 14xy(8x2y + 1) — Incorrect (incorrect factorization).
Step 5: Verification
The original expression is 16x3y2 + 14xy. Expanding 2xy(8x2y + 7):
2xy(8x2y + 7)
= 2xy ⋅ 8x2y + 2xy ⋅ 7
= 16x3y2 + 14xy
The factored form is correct.
Final Answer: B) 2xy(8x2y + 7).
5th Question
Question: A veterinarian recommends that each day a certain rabbit should eat 25 calories per pound of the rabbit’s weight, plus an additional 11 calories. Which equation represents this situation, where c is the total number of calories the veterinarian recommends the rabbit should eat each day if the rabbit’s weight is x pounds?
A) c = 25x
B) c = 36x
C) c = 11x + 25
D) c = 25x + 11
Choice D is correct. It’s given that a veterinarian recommends that each day the rabbit should eat 25 calories per pound of the rabbit’s weight, plus an additional 11 calories. If the rabbit’s weight is x pounds, then multiplying 25 calories per pound by the rabbit’s weight, x pounds, yields 25x calories. Adding the additional 11 calories that the rabbit should eat each day yields 25x + 11 calories. It’s given
that c is the total number of calories the veterinarian recommends the rabbit should eat each day if the rabbit’s weight is x pounds. Therefore, this situation can be represented by the equation c = 25x + 11.
Choice A is incorrect. This equation represents a situation where a veterinarian recommends that each day the rabbit should eat 25 calories per pound of the rabbit’s weight.
Choice B is incorrect. This equation represents a situation where a veterinarian recommends that each day the rabbit should eat 25 + 11, or 36, calories per pound of the rabbit’s weight.
Choice C is incorrect. This equation represents a situation where a veterinarian recommends that each day the rabbit should eat 11 calories per pound of the rabbit’s weight, plus an additional 25
calories.
Problem:
A veterinarian recommends a rabbit consume calories daily based on its weight x (in pounds). The rabbit should eat 25 calories per pound of its weight plus an additional 11 calories. Which equation best represents this situation?
Step 1: Understand the problem
We are given:
1) Calories per pound: The rabbit eats 25 calories for each pound of its weight.
~ This means if the rabbit weighs x pounds, it will eat 25x calories.
2) Additional calories: Regardless of the rabbit’s weight, an extra 11 calories are added to its diet.
~ This adds a constant value of 11.
3) Total calories c: The total number of calories c is the sum of the weight-dependent calories 25x and the additional calories 11.
Thus, the relationship can be modeled as:
c = 25x + 11
Step 2: Analyze the options
Option A: c = 25x
~ This equation includes only the calories based on weight, 25x, but it does not account for the additional 11 calories. (Incorrect.)
Option B: c = 36x
~ This equation incorrectly assumes that the rabbit consumes 36 calories per pound of its weight, which contradicts the problem. (Incorrect.)
Option C: c = 11x + 25
~ This equation incorrectly assumes that the rabbit consumes 11 calories per pound of its weight, with an additional 25 calories. This swaps the roles of the coefficients and does not match the problem. (Incorrect.)
Option D: c = 25x + 11
~ This equation correctly accounts for the 25 calories per pound (25x) and the additional 11 calories. (Correct.)
Step 3: Verification
To verify, substitute specific values of xxx (weight) into the correct equation c = 25x + 11 and ensure the result aligns with the problem.
Example:
If the rabbit weighs 3 pounds (x = 3), the total calories are:
c = 25(3) + 11
c = 75 + 11
c = 86
The rabbit should eat 86 calories.
This calculation matches the problem description.
Final Answer: D) c = 25x + 11.
6th Question
Question: Which expression is equivalent to 9x2 + 5x?
A) x(9x + 5)
B) 5x(9x + 1)
C) 9x(x + 5)
D) x2(9x + 5)
Choice A is correct. Since x is a factor of each term in the given expression, the expression is equivalent to x(9x) + x(5), or x(9x + 5).
Choice B is incorrect. This expression is equivalent to 45x2 + 5x, not 9x2 + 5x.
Choice C is incorrect. This expression is equivalent to 9x2 + 45x, not 9x2 + 5x.
Choice D is incorrect. This expression is equivalent to 9x3 + 5x2, not 9x2 + 5x.
Step 1: Understand factoring
Factoring is the process of rewriting a polynomial as the product of simpler expressions. In 9x2 + 5x, observe that:
1) Both terms (9x2 and 5x) have a common factor, which is x.
2) Factoring x out of each term, we get:
9x2 + 5x = x(9x + 5)
Thus, the factored form of 9x2 + 5x is x(9x + 5).
Step 2: Analyze the options
Option A: x(9x + 5)
~ This matches our factored form. (Correct.)
Option B: 5x(9x + 1)
~ This factors 5x incorrectly and introduces a term 9x + 1, which is not equivalent to the original expression. (Incorrect.)
Option C: 9x(x + 5)
~ This assumes 9x is a common factor, which it is not. The original expression does not have 9x in both terms. (Incorrect.)
Option D: x2(9x + 5)
~ This introduces an extra x, changing the degree of the polynomial. The original expression is quadratic (9x2 + 5x), but this form makes it cubic (x3). (Incorrect.)
Step 3: Verification
Expand x(9x + 5) to ensure it equals the original expression:
x(9x + 5) = 9x2 + 5x
This confirms the factorization is correct.
Final Answer: A) x(9x + 5).
7th Question
Question: In triangle ABC, the measure of angle B is 52° and the measure of angle C is 17°. What is the measure of angle A?
A) 21°
B) 35°
C) 69°
D) 111°
Choice D is correct. The sum of the angle measures of a triangle is 180o. Adding the measures of angles B and C gives 52 + 17 = 69o. Therefore, the measure of angle A is 180 – 69 = 111o.
Choice A is incorrect and may result from subtracting the sum of the measures of angles B and C from 90o, instead of from 180o.
Choice B is incorrect and may result from subtracting the measure of angle C from the measure of angle B.
Choice C is incorrect and may result from adding the measures of angles B and C but not subtracting the result from 180o.
Problem:
In triangle △ABC, the measures of angles B and C are given as 52∘ and 17∘, respectively. We need to determine the measure of angle A.
Step 1: Recall the triangle sum property
The sum of the interior angles of any triangle is always 180∘.
Sum of angles: A + B + C = 180∘
Step 2: Substitute known values
Given:
B = 52∘, C = 17∘
Substitute these values into the triangle sum property:
A + 52 + 17 = 180
Step 3: Simplify the equation
Combine 52 and 17:
A + 69 = 180
Solve for A by subtracting 69 from both sides:
A = 180 − 69
A = 111∘
Step 4: Verification
To verify, calculate the sum of all angles in the triangle:
A + B + C
= 111 + 52 + 17
= 180.
This confirms the solution is correct.
Final Answer: D) The measure of angle A is: 111∘.
8th Question
x = 8
y = x2 + 8
Question: The graphs of the equations in the given system of equations intersect at the point (x, y) in the xy-plane. What is the value of y?
A) 8
B) 24
C) 64
D) 72
Choice D is correct. Since the graphs of the equations in the given system intersect at the point (x, y), the point (x, y), represents a solution to the given system of equations. The first equation of the given system of equations states that x = 8. Substituting 8 for x in the second equation of the given system of equations yields y = 82 + 8, or y = 72. Therefore, the value of y is 72.
Choice A is incorrect. This is the value of x, not y.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the problem
The first equation states that x = 8, meaning that the x-coordinate of the intersection point is fixed at 8.
The second equation expresses y in terms of x:
y = x2 + 8
Since x = 8, substitute this value into the second equation to determine y.
Step 2: Substitute x = 8 into y = x2 + 8
Replace x with 8 in the second equation:
y = 82 + 8
Simplify the equation:
y = 64 + 8
y = 72
Step 3: Verification
Check whether x = 8 and y = 72 satisfy both equations:
1) x = 8: Clearly true.
2) y = x2 + 8: Substituting x = 8,
y = 82 + 8
y = 72
Both equations are satisfied. Thus, the solution is verified.
Final Answer: The value of y is: 72.
9th Question
Question:
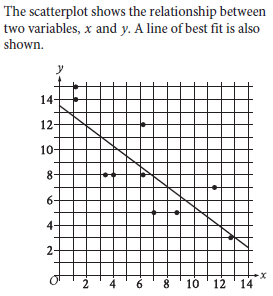
Which of the following equations best represents the line of best fit shown?
A) y = 13.5 + 0.8x
B) y = 13.5 − 0.8x
C) y = −13.5 + 0.8x
D) y = −13.5 − 0.8x
Choice B is correct. The line of best fit shown intersects the y-axis at a positive y-value and has a negative slope. The graph of an equation of the form y = a + bx, where a and b are constants, intersects the y-axis at a y-value of a and has a slope of b. Of the given choices, only choice B represents a line that intersects the y-axis at a positive y-value, 13.5, and has a negative slope, -0.8.
Choice A is incorrect. This equation represents a line that has a positive slope, not a negative slope.
Choice C is incorrect. This equation represents a line that intersects the y-axis at a negative y-value, not a positive y-value, and has a positive slope, not a negative slope.
Choice D is incorrect. This equation represents a line that intersects the y-axis at a negative y-value, not a positive y-value.
Step 1: Analyze the line of best fit
The line of best fit is a downward-sloping line, indicating a negative correlation between x and y. This means the slope (m) of the line is negative.
From the options provided, only equations with a negative slope (−0.8x) are valid:
~ Option B: y = 13.5 − 0.8x
~ Option D: y = −13.5 − 0.8x
We can now eliminate Options A and C because their slopes (+0.8x) are positive, which contradicts the negative slope of the line.
Step 2: Examine the y-intercept
The y-intercept is the point where the line crosses the y-axis (x = 0). From the graph, the y-intercept appears to be approximately 13.5.
~ Option B: y = 13.5 − 0.8x
Here, the y-intercept is +13.5.
~ Option D: y = −13.5 − 0.8x
Here, the y-intercept is −13.5.
Since the y-intercept in the graph is clearly positive, Option D can be eliminated.
Step 3: Verify the slope
The slope of the line (m) is the rate of change of y with respect to x. It can be calculated using two points on the line. From the graph, two points on the line are approximately:
~ Point 1: (0, 13.5)
~ Point 2: (10, 5.5)
Using the slope formula:
m = Δy/Δx
m = y2 – y1 / x2 – x1
Substitute (x1, y1) = (0, 13.5) and (x2, y2) = (10, 5.5):
m = 5.5 – 13.5 / 10 – 0
m = -8/10
m = -0.8.
The slope of the line is −0.8, which matches the slope in Option B.
Final Answer: The equation that best represents the line of best fit is: B) y = 13.5 – 0.8x.
10th Question
Question:
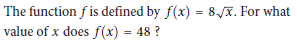
A) 6
B) 8
C) 36
D) 64
Choice C is correct.
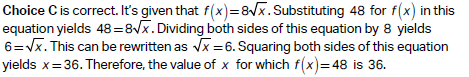
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
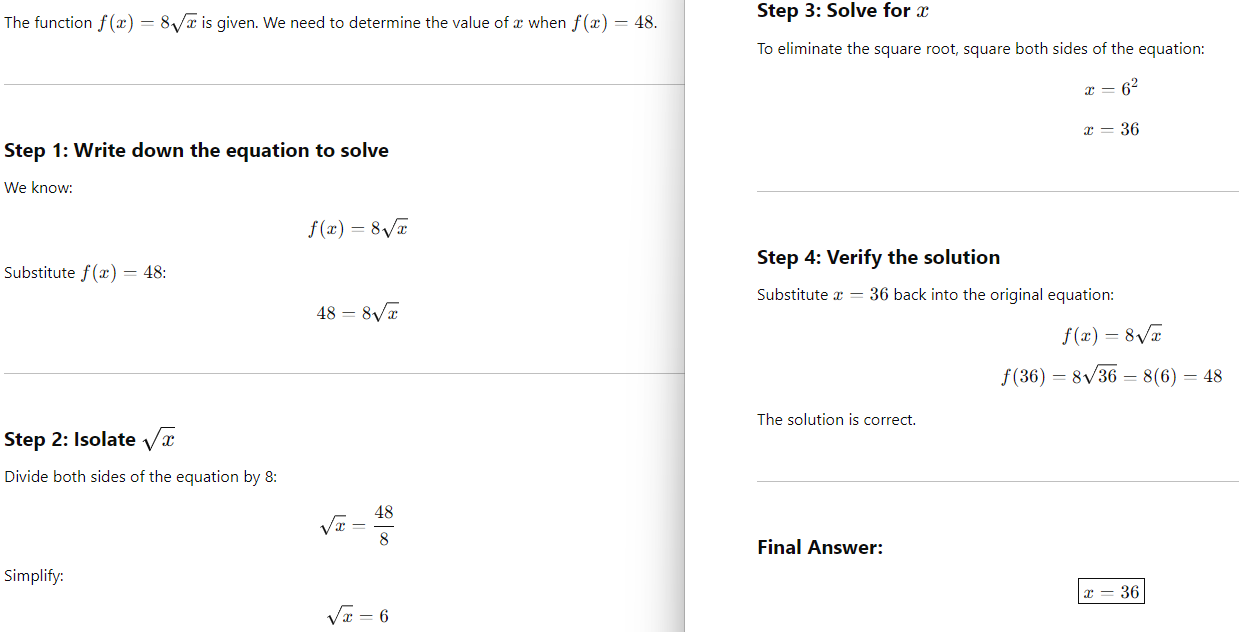
Final Answer: Option C.
11th Question
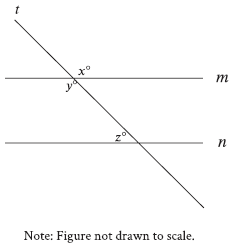
Question: In the figure, lines m and n are parallel. If x = 6k + 13 and y = 8k − 29, what is the value of z?
A) 3
B) 21
C) 41
D) 139
Choice C is correct. Vertical angles, which are angles that are opposite each other when two lines intersect, are congruent. The figure shows that lines t and m intersect. It follows that the angle with measure xo and the angle with measure yo are vertical angles, so x = y. It’s given that x = 6k + 13 and y = 8k – 29. Substituting 6k + 13 for x and 8k – 29 for y in the equation x = y yields 6k + 13 = 8k – 29. Subtracting 6k from both sides of this equation yields 13 = 2k – 29. Adding 29 to both sides of this equation yields 42 = 2k, or 2k = 42. Dividing both sides of this equation by 2 yields k = 21. It’s given that lines m and n are parallel, and the figure shows that lines m and n are intersected by a transversal, line t. If two parallel lines are intersected by a transversal, then the same-side interior angles are supplementary. It follows that the same-side interior angles with measures yo and zo are supplementary, so y + z = 180. Substituting 8k – 29 for y in this equation yields 8k – 29 + z = 180. Substituting 21 for k in this equation yields 8(21) – 29 + z = 180, or 139 + z = 180. Subtracting 139 from both sides of this equation yields z = 41. Therefore, the value of z is 41.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect. This is the value of k, not z.
Choice D is incorrect. This is the value of x or y, not z.
Problem Restatement:
We are working with parallel lines m and n intersected by a transversal t. In the diagram, we are given three angles: x∘, y∘, and z∘. Angles x∘ and y∘ are vertical angles, meaning they are equal. The problem states that x = 6k + 13 and y = 8k − 29, and we need to find the value of z.
Key geometry property:
We also know that x = y.
When a transversal intersects two parallel lines, the same-side interior angles are supplementary, meaning:
y + z =180∘
Step-by-Step Explanation:
Step 1: Set up the equation using x = y
Since x∘ and y∘ are vertical angles:
6k + 13 = 8k − 29
Step 2: Solve for k
1) Subtract 6k from both sides: 13 = 2k – 29
2) Add 29 to both sides: 42 = 2k
3) Divide by 2: k = 21
Step 3: Find z:
1) Set up the supplementary angle equation:
Since y and z are same-side interior angles:
y + z = 180
2) Substitute the expression for y:
Given y = 8k − 29, substitute this into the equation:
(8k − 29) + z =180
3) Solve for z:
Rearrange the equation to isolate z:
z = 180 − (8k − 29)
Simplify the subtraction:
z = 180 − 8k + 29
z = 209 – 8k
4) Substitute k = 21:
It is given that k = 21. Substitute this value into the equation for z:
z = 209 − 8(21)
Perform the multiplication:
z = 209 − 168
Simplify:
z = 41
Final Verification:
Check the geometry property:
Using k = 21, calculate y:
y = 8k − 29
y = 8(21) − 29
y = 168 − 29
y = 139
The sum of y and z should be 180:
y + z = 139 + 41 = 180
The calculation is consistent with the geometry rule.
Final Answer: C) z = 41∘.
12th Question
-3x + 21px = 84
Question: In the given equation, p is a constant. The equation has no solution. What is the value of p?
A) 0
B) 1/7
C) 4/3
D) 4
Choice B is correct. A linear equation in one variable has no solution if and only if the equation is false; that is, when there is no value of x that produces a true statement. It’s given that in the equation -3x + 21px = 84, p is a constant and the equation has no solution for x. Therefore, the value of the constant p is one that results in a false equation. Factoring out the common factor of -3x on the left-hand side of the given equation yields -3x(1 – 7p) = 84. Dividing both sides of this equation by -3 yields x(1 – 7p) = -28. Dividing both sides of this equation by (1 – 7p) yields x = -28/1 – 7p. This equation is false if and only if 1 – 7p = 0. Adding 7p to both sides of 1 – 7p = 0 yields 1 = 7p. Dividing both sides of this equation by 7 yields 1/7 = p. It follows that the equation x = -28/1 – 7p is false if and only if p = 1/7. Therefore, the given equation has no solution if and only if the value of p is 1/7.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Restatement:
We are given the equation:
−3x + 21px = 84
We need to determine the value of p such that the equation has no solution.
Key Concept: No Solution for an Equation
An equation has no solution when simplifying it leads to a contradiction, such as:
0 = a non-zero constant (e.g., 0 = 5).
This problem happens if the terms involving x are completely canceled out (i.e., their coefficients add to zero), leaving a false statement.
Step-by-Step Explanation:
1) Combine like terms:
Factor x from the terms on the left-hand side: (−3 + 21p)x = 84
2) Analyze the equation for no solution:
For the equation to have no solution, the coefficient of x must be zero. This is because, if (−3 + 21p) = 0, the equation becomes:
0 ⋅ x = 84
which simplifies to:
0 = 84
This is a contradiction, meaning the equation has no solution.
3) Solve for p:
Set the coefficient of x equal to zero:
−3 + 21p = 0
Solve for p:
21p = 3
p = 3/21
p = 1/7.
Verification:
Substitute p = 1/7 back into the coefficient of x
−3 + 21 ⋅ 1/7
= −3 + 3 = 0
This confirms that the coefficient of x becomes zero, leading to the contradiction 0 = 84. Therefore, the equation has no solution.
Final Answer: B) p = 1/7.
How to Identify That the Equation is False and Has No Solution:
1. The Variable Cancels Out Completely
If, during simplification, the terms involving the variable x (or any other variable) cancel out entirely, leaving behind an equation involving only constants, there are two possibilities:
~ False Statement: If the remaining constants form a contradiction (e.g., 0 = 5), the equation has no solution.
~ True Statement: If the remaining constants form a true statement (e.g., 0 = 0), the equation has infinitely many solutions.
The original equation is:
−3x + 21px = 84
Here, the left-hand side has terms involving x: −3x and 21px. To factor x out, we combine the terms:
(−3 + 21p)x = 84
Now, notice:
~ If −3 + 21p ≠ 0, the equation would still depend on x, and we could solve for x.
~ If −3 + 21p = 0, the term (−3 + 21p)x becomes 0 ⋅ x = 0, leaving:
0 = 84
This is a contradiction because 0 ≠ 84. Therefore, the equation has no solution only when −3 + 21p = 0.
Key Takeaways:
1) We set −3 + 21p = 0 because a zero coefficient for x removes x from the equation, leaving only constants.
2) If the remaining equation involving constants is false (e.g., 0 = 84), the equation has no solution.
3) To quickly identify this, look for when the coefficient of the variable cancels out to zero and check if it creates a contradiction in the remaining equation.
This is how we logically determine that −3 + 21p = 0 is the key step to finding the value of p for which the equation has no solution.
13th Question
f(x) = (x − 10)(x + 13)
Question: The function f is defined by the given equation. For what value of x does f(x) reach its minimum?
A) -130
B) -13
C) -23/2
D) -3/2
Choice D is correct. It’s given that f(x) = (x – 10)(x + 13), which can be rewritten as f(x) = x2 + 3x – 130. Since the coefficient of the x2-term is positive, the graph of y = f(x) in the xy-plane opens upward and reaches its minimum value at its vertex. The x-coordinate of the vertex is the value of x such that f(x) reaches its minimum. For an equation in the form f(x) = ax2 + bx + c, where a, b, and c are constants, the x-coordinate of the vertex is –b/2a. For the equation f(x) = x2 + 3x – 130, a = 1, b = 3, and c = -130. It follows that the x-coordinate of the vertex is (-3/2(1), or -3/2, therefore, f(x) reaches its minimum when the value of x is -3/2.
Alternate approach: The value of x for the vertex of a parabola is the x-value of the midpoint between the two x-intercepts of the parabola. Since it’s given that f(x) = (x – 10)(x + 13), it follows that the two x-intercepts of the graph of y = f(x) in the xy-plane occur when x = 10 and x = -13, or at the points (10, 0) and (-13, 0). The midpoint between two points, (x1, y1) and (x2, y2), is (x1 + x2 divided by 2, y1 + y2 divided by 2). Therefore, the midpoint between (10, 0) and (-13, 0) is (10 +(13)/2, 0 + 0/2), or (-3/2, 0). It follows that f(x) reaches its minimum when the value of x is -3/2.
Choice A is incorrect. This is the y-coordinate of the y-intercept of the graph of y = f(x) in the xy-plane.
Choice B is incorrect. This is one of the x-coordinates of the x-intercepts of the graph of y = f(x) in the xy-plane.
Choice C is incorrect and may result from conceptual or calculation errors.
Question Analysis
The function f(x) = (x − 10)(x +13) is a quadratic function, which forms a parabola when graphed. Since the coefficient of x2 is positive (as we’ll see after expansion), the parabola opens upward, meaning it has a minimum value at its vertex.
We are tasked with finding the value of x where f(x) reaches its minimum, which is the x-coordinate of the vertex.
Step-by-Step Explanation
Step 1: Understand the standard form of a quadratic function
The general form of a quadratic function is:
f(x) = ax2 + bx + c
For a parabola, the x-coordinate of the vertex can be found using the formula:
x = −b/2a
Where a is the coefficient of x2, and b is the coefficient of x.
Step 2: Expand the given equation
The given equation is in factored form:
f(x) = (x − 10)(x +13)
Expand it to express it in standard form:
f(x) = x2 + 13x − 10x − 130
f(x) = x2 + 3x − 130
Here:
~ a = 1 (coefficient of x2),
~ b = 3 (coefficient of x),
~ c = −130 (constant term).
Step 3: Use the vertex formula
The x-coordinate of the vertex is:
x = −b/2a
Substitute b = 3 and a = 1 into the formula:
x = −3/2(1)
x = −3/2
Step 4: Verify the vertex
Since the parabola opens upward (a = 1 > 0), this x-coordinate represents the point where f(x) reaches its minimum value. At x = −3/2, the function achieves its lowest value.
Final Answer: The value of x where f(x) reaches its minimum is:
x = −3/2.
Alternate Approach:

Why This Works
The midpoint method is valid because the parabola is symmetric. The x-coordinate of the vertex lies exactly between the two x-intercepts, so the midpoint formula provides a quick way to find it without converting to standard form.
14th Question
2x – y > 883
Question: For which of the following tables are all the values of x and their corresponding values of y solutions to the given inequality?
A)
| x | y |
|---|---|
| 440 | 0 |
| 441 | -2 |
| 442 | -4 |
B)
| x | y |
|---|---|
| 440 | 0 |
| 442 | -2 |
| 441 | -4 |
C)
| x | y |
|---|---|
| 442 | 0 |
| 440 | -2 |
| 441 | -4 |
D)
| x | y |
|---|---|
| 442 | 0 |
| 441 | -2 |
| 440 | -4 |
Choice D is correct. All the tables in the choices have the same three values of x, 440, 441, and 442, so each of the three values of x can be substituted in the given inequality to compare the corresponding values of y in each of the tables. Substituting 440 for x in the given inequality yields 2(440) – y > 883, or 880 – y > 883. Subtracting 880 from both sides of this inequality yields –y > 23. Dividing both sides of this inequality by -1 yields y < – 3. Therefore, when x = 440, the corresponding value of y must be less than -3. Substituting 441 for x in the given inequality yields 2(441) – y > 883, or 882 – y > 883. Subtracting 882 from both sides of this inequality yields –y > 1. Dividing both sides of this inequality by -1 yields y < -1. Therefore, when x = 441, the corresponding value of y must be less than -1. Substituting 442 for x in the given inequality yields 2(442) – y > 883, or 884 – y > 883. Subtracting 884 from both sides of this inequality yields –y > -1. Dividing both sides of this inequality by -1 yields y < 1. Therefore, when x = 442, the corresponding value of y must be less than 1. For the table in choice D, when x = 440, the corresponding value of y is -4, which is less than -3; when x = 441, the corresponding value of y is -2, which is less than -1; when x = 442, the corresponding value of y is 0, which is less than 1. Therefore, the table in choice D gives values of x and their corresponding values of y that are all solutions to the given inequality.
Choice A is incorrect. When x = 440, the corresponding value of y in this table is 0, which isn’t less than -3.
Choice B is incorrect. When x = 440, the corresponding value of y in this table is 0, which isn’t less than -3.
Choice C is incorrect. When x = 440, the corresponding value of y in this table is -2, which isn’t less than -3.
Step-by-Step Solution
Step 1: Analyze the inequality
The given inequality is:
2x − y > 883
We can rewrite it in terms of y to make the inequality easier to check:
y < 2x − 883
This means that for any value of x, the corresponding value of y must be less than 2x − 883 for the inequality to hold.
Step 2: Check each table
We will check whether all the values of x and y in each table satisfy the inequality y < 2x − 883.
Option A)
| x | y |
|---|---|
| 440 | 0 |
| 441 | -2 |
| 442 | -4 |
For x = 440:
y < 2(440) − 883
y < 880 − 883
y < −3
The given y = 0, but 0 ≮ −3. This does not satisfy the inequality.
Since the first row of Table A does not satisfy the inequality, Table A is invalid.
Option B)
| x | y |
|---|---|
| 440 | 0 |
| 442 | -2 |
| 441 | -4 |
For x = 440:
y < 2(440) − 883
y < 880 – 883
y < −3y
The given y = 0, but 0 ≮ −3. This does not satisfy the inequality.
Since the first row of Table B does not satisfy the inequality, Table B is invalid.
Option C)
| x | y |
|---|---|
| 442 | 0 |
| 440 | -2 |
| 441 | -4 |
For x = 442:
y < 2(442) − 883
y < 884 − 883
y < 1
The given y = 0, and 0 < 1. This satisfies the inequality.
For x = 440:
y < 2(440) − 883
y < 880 – 883
y < −3
The given y = −2, but −2 ≮ −3. This does not satisfy the inequality.
Since the second row of Table C does not satisfy the inequality, Table C is invalid.
Option D)
| x | y |
|---|---|
| 440 | 0 |
| 441 | -2 |
| 442 | -4 |
For x = 442:
y < 2(442) − 883
y < 884 – 883
y < 1
The given y = 0, and 0 < 1. This satisfies the inequality.
For x = 441 (second row):
y < 2(441) − 883
y < 882 − 883
y < −1
The given y = −2, and −2 < −1. This satisfies the inequality.
For x = 441 (third row):
y < 2(441) − 883
y < 882 – 883
y < −1
The given y = −4, and −4 < −1. This satisfies the inequality.
All rows of Table D satisfy the inequality.
Final Answer: Option D.
15th Question
5y = 10x + 11
-5y = 5x – 21
Question: The solution to the given system of equations is (x, y). What is the value of 30x?
A) 10
B) 20
C) 30
D) 40
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 20. Adding the first equation to the second equation in the given system yields 5y – 5y = 10x + 5x + 11 – 21, or 0 = 15x – 10. Adding 10 to both sides of this equation yields 10 = 15x. Multiplying both sides of this equation by 2 yields 20 = 30x. Therefore, the value of 30x is 20.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
Step 1: Add the two equations to eliminate y
The two equations are:
5y = 10x + 11 (1)
−5y = 5x − 21 (2)
When we add equations (1) and (2), the 5y terms cancel out:
5y + (−5y) = (10x + 11) + (5x − 21)
Simplify:
0 = 15x − 10
Step 2: Solve for x
Rearrange the equation to solve for x:
15x = 10
Divide both sides by 15:
x = 10/15
x = 2/3
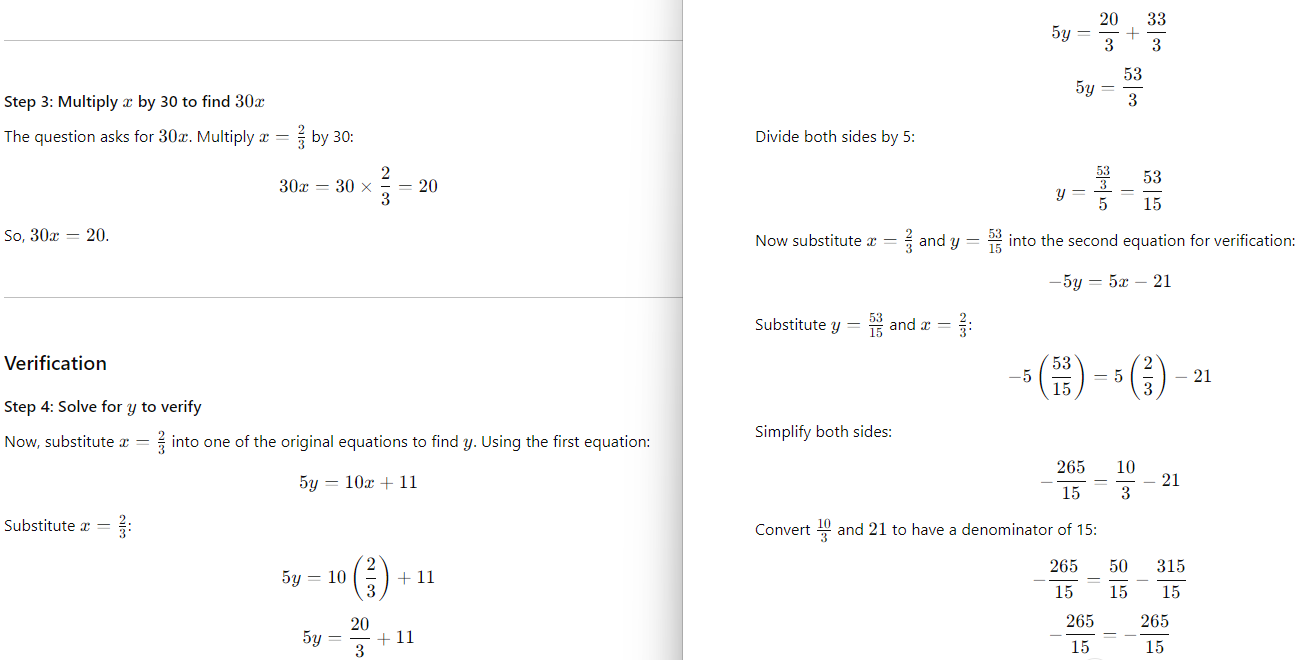
Both sides match, confirming the solution is correct.
Final Answer: B) 20.
16th Question
(x – 2) – 4(y + 7) = 117
(x – 2) + 4(y + 7) = 442
Question: The solution to the given system of equations is (x, y). What is the value of 6(x − 2)?
A) 1344
B) 1455
C) 1566
D) 1677
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 1,677. Adding the first equation to the second equation in the given system yields (x – 2) + (x – 2) + (-4)(y + 7) = 117 + 442, or 2(x – 2) = 559. Multiplying both sides of this equation by 3 yields 6(x – 2) = 1,677. Therefore, the value of 6(x – 2) is 1,677.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
Step 1: Simplify both equations
Let us rewrite the equations for clarity.
Equation 1: (x − 2) − 4(y + 7) = 117
Distribute the −4:
(x − 2) − 4y − 28 = 117
Simplify:
(x − 2) − 4y = 145 (1)
Equation 2: (x − 2) + 4(y + 7) = 442
Distribute the +4:
(x − 2) + 4y + 28 = 442
Simplify:
(x − 2) + 4y = 414 (2)
Step 2: Add and subtract the equations
We now solve for (x − 2) and y.
Step 2.1: Add the equations
[(x − 2) − 4y] + [(x − 2) + 4y] = 145 + 414
The 4y terms cancel out:
2(x − 2) = 559
Divide both sides by 2:
x − 2 = 279.5 (3)
Step 2.2: Subtract the equations
[(x − 2) +4 y] − [(x − 2) − 4y] = 414 − 145
The (x − 2) terms cancel out:
8y = 269
Divide both sides by 8:
y = 269/8 = 33.625 (4)
Step 3: Solve for 6(x − 2)
The question asks for 6(x − 2). Using (x − 2) = 279.5 from Equation (3):
6(x − 2) = 6 × 279.5 = 1677
Verification
Step 4: Verify the solution
Using (x − 2) = 279.5 and y = 33.625, substitute into the original equations.
Equation 1: (x − 2) − 4(y + 7) = 117
Substitute (x − 2) = 279.5 and y = 33.625:
279.5 − 4(33.625 + 7) = 279.5 − 4(40.625)
279.5 − 162.5 = 117
This is correct.
Equation 2: (x − 2) + 4(y + 7) = 442
Substitute (x − 2) = 279.5 and y = 33.625:
279.5 + 4(33.625 + 7) = 279.5 + 4(40.625)
279.5 + 162.5 = 442
This is correct.
Final Answer: D) 1677.
17th Question
Question:

Choice B is correct.


Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown
We are tasked to find the length of side AC in triangle ABC:
~ Since this is a right triangle, we can use the Pythagorean Theorem:
AC2 = AB2 + BC2
~ ∠B is a right angle, so the triangle is a right triangle.
Step-by-Step Solution
Step 1: Apply the Pythagorean Theorem
The formula for the hypotenuse in a right triangle is:
AC2 = AB2 + BC2
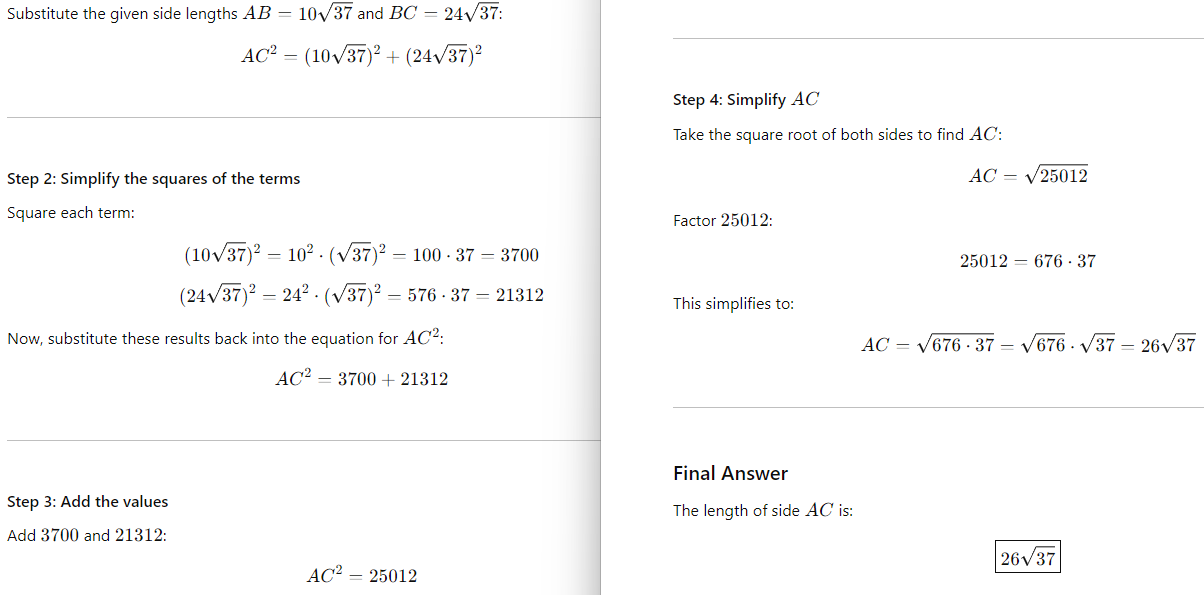
Let’s Verify:

Final Answer: Option B.
18th Question
f(x) = (1.84)x/4
Question: The function f is defined by the given equation. The equation can be rewritten as f(x) = (1+P/100)x, where p is a constant. Which of the following is closest to the value of p?
A) 16
B) 21
C) 46
D) 96
Choice A:
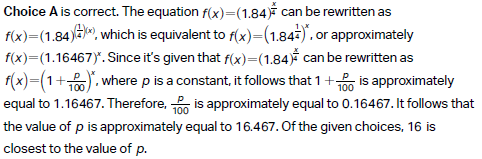
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown
The function f(x) is defined as:
f(x) = (1.84)x/4
The goal is to rewrite it in the form:
f(x) = (1 + P/100)x
where P is a percentage. We need to determine the value of P.
Step-by-Step Solution
Step 1: Compare the given equation to the target form
The key is to express (1.84)x/4 in the form (1 + P/100)x. To do this, we rewrite (1.84)x/4 so that the base is raised to x, matching the target form.
Step 2: Rewrite the exponent
The given equation is:
f(x) = (1.84)x/4
Using the rule of exponents (ab)c = ab ⋅ c, rewrite (1.84)x/4 as:
f(x) = ((1.84)1/4)x
Here, (1.84)1/4 becomes the new base.
Step 3: Compute (1.84)1/4
To find (1.84)1/4, calculate the fourth root of 1.84. Using a calculator
(1.84)1/4 ≈ 1.16
So, the equation becomes:
f(x) = (1.16)x
Step 4: Express 1.16 in the form 1 + P/100
The base 1.16 can be written as:
1.16 = 1 + 0.16
Here, 0.16 is equivalent to 16/100, so:
1.16 = 1 + 16/100
Thus, P = 16.
Verification
Substitute P = 16 back into the rewritten equation:
f(x) = (1 + 16/100)x
f(x) = (1.16)x
This matches the form derived earlier, confirming that P = 16 is correct.
Final Answer: The value of P is closest to: A) 16.
19th Question
Question:

A) f(0) = 24
B) f(0) = −24
C) a > b
D) a < b
Choice D is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Breakdown
The function f(x) is defined as:

Step 2: Analyze f(24) < 0
For x = 24, the equation becomes:

Final Answer: D) a < b.
20th Question
Question:

Choice A is correct.

Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Some common Concepts:

Let’s solve it!
Step 1: Understanding the problem

Final Answer: Option A.
21th Question
Question:

A) 4
B) 8
C) 9
D) 16
Choice B is correct. Let x represent the side length, in cm, of each square base. If the two prisms are glued together along a square base, the resulting prism has a surface area equal to twice the surface area of one of the prisms, minus the area of the two square bases that are being glued together, which yields 2K – 2x2 cm2. It’s given that this resulting surface area is equal to 92K/47 cm2, so 2K – 2x2 = 92K/47. Subtracting 92K/47 from both sides of this equation yields 2K – 92K/47 – 2x2 = 0. This equation can be rewritten by multiplying 2K on the left-hand side by 47/47, which yields 94K/47 – 94K/47 – 2x2, or 2K/47 – 2x2 = 0. Adding 2x2 to both sides of this equation yields 2K/47 = 2x2. Multiplying both sides of this equation by 47/2 yields K = 47x2. The surface area K, in cm2, of each rectangular prism is equivalent to the sum of the areas of the two square bases and the areas of the four lateral faces. Since the height of each rectangular prism is 90 cm and the side length of each square base is x cm, it follows that the area of each square base is x2 cm2 and the area of each lateral face is 90x cm2. Therefore, the surface area of each rectangular prism can be represented by the expression 2x2 + 4(90x), or 2x2 + 360x. Substituting this expression for K in the equation K = 47x2 yields 2x2 + 360x = 47x2. Subtracting 2x2 and 360x from both sides of this equation yields 0 = 45x2 – 360x. Factoring x from the right-hand side of this equation yields 0 = x(45x – 360). Applying the zero product property, it follows that x = 0 and 45x – 360 = 0. Adding 360 to both sides of the equation 45x – 360 = 0 yields 45x = 360. Dividing both sides of this equation by 45 yields x = 8. Since the side length of a rectangular prism can’t be 0, the length of each square base is 8 cm.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
We are solving for the side length x, in cm, of each square base of two identical rectangular prisms. The problem provides the following information:
1) Height of each prism: 90 cm,
2) Surface area of each prism: K cm2,
3) When the prisms are glued together along one square base, the resulting prism has a surface area of 92K/47 cm2.
We must find the side length x of the square base.
Step 1: Surface Area of One Rectangular Prism
The surface area K of one rectangular prism is calculated as:
K = 2(Area of Square Base) + 4(Area of Rectangular Faces).
Here:
~ The area of the square base = x2,
~ The area of each rectangular face = x × 90 = 90x.
~ Substitute these into the formula for K:
K = 2x2 + 4(90x).
Simplify:
K = 2x2 + 360x.
Step 2: Surface Area of the Combined Prism
When the two prisms are glued together along one square base:
~ The glued square base is no longer exposed.
~ The total surface area is therefore reduced by 2x2 (the area of the two glued square bases).
The surface area of the resulting prism is:
New Surface Area = 2K − 2x2.
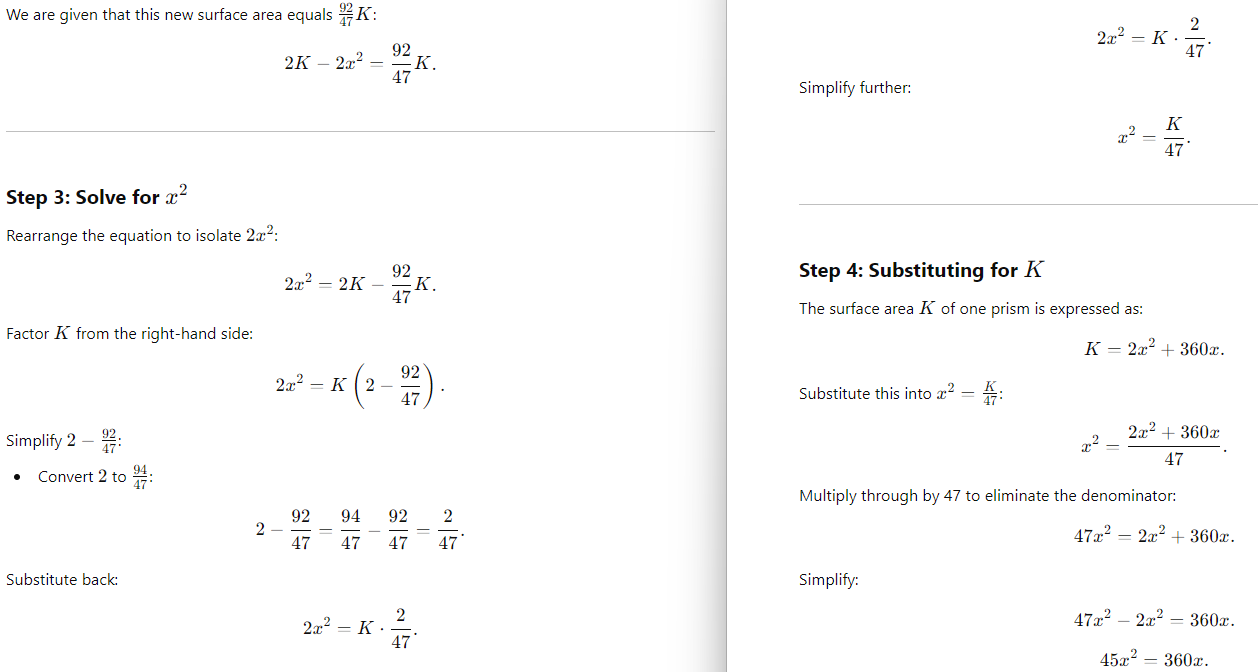

Final Answer: B) 8.
Key Points: x(45x – 360) = 0
In the final solution, x is the side length of the square base. It cannot be “nothing” because the rectangular prism exists, and its square base must have a real, non-zero side length. Factoring helps simplify the problem, but x still represents a meaningful value (other than zero) in this context.
1) x = 0
2) 45x – 360 = 0
This means that the product of x and (45x − 360) is equal to zero. For a product to equal zero, at least one of the factors must be zero. Therefore, we consider the two possibilities. This is called the zero-product property.
The first equation, x = 0, is discarded for being physically meaningless in this scenario. This does not mean x disappears — it simply means that the first solution does not apply to the problem. The second equation, 45x − 360 = 0, is then solved for x, giving us the correct side length.
Why is x = 0 not valid in this problem?
In the context of the problem, x represents the side length of the square base of the prism. A side length cannot be zero because:
~ A square with a side length of zero would not exist (its area would also be zero).
~ This would contradict the problem’s setup, which involves actual rectangular prisms.
So, even though x = 0 is mathematically valid as a solution to the equation x(45x − 360) = 0, it does not make sense in the real-world context of this problem. We exclude x = 0 as a solution because it is not physically meaningful.
But 45x – 360, where x is the side length of the square base. It cannot be “nothing” because the rectangular prism exists, and its square base must have a real, non-zero side length.
Summary:
1) Factoring gives two possibilities: x = 0 and 45x − 360 = 0
2) x = 0 is discarded because a side length cannot be zero.
3) We solve 45x − 360 = 0 because it represents the real-world side length.
4) x still exists and has a valid value in the solution — it is not “nothing.”
22th Question
Question: 210 is p% greater than 30. What is the value of p?
A) 600
B) 630
C) 660
D) 690
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A: The correct answer is 600. It’s given that 210 is p% greater than 30. It follows that 210 = (1 + P/100)(30). Dividing both sides of this equation by 30 yields 7 = 1 + P/100. Subtracting 1 from both sides of this equation yields 6 = P/100. Multiplying both sides of this equation by 100 yields p = 600. Therefore, the value of p is 600.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the meaning of the question
The question states that 210 is p% greater than 30. This means:
210 = 30 + p/100 ⋅ 30.
Here:
~ 30 is the original value.
~ p/100 ⋅ 30 represents p% of 30 (the increase).
~ Adding these together gives the new value, 210.
Step 2: Write the equation
The equation based on the above interpretation is:
210 = 30 + p/100 ⋅ 30.
Step 3: Isolate p/100 ⋅ 30
Subtract 30 from both sides of the equation:
210 − 30 = p/100 ⋅ 30.
180 = p/100 ⋅ 30.
Step 4: Solve for p/100
Divide both sides of the equation by 30 to isolate p/100:
p/100 = 180/30.
p/100 = 6.
Step 5: Solve for p
Multiply both sides of the equation by 100 to solve for p:
p = 6 ⋅ 100.
Step 6: Verify the solution
If p = 600, then 600% of 30 is:
600/100 ⋅ 30
= 6 ⋅ 30
=180.
Adding 180 to the original value of 30 gives:
30 + 180 = 210.
This matches the value in the question, so the solution is verified.
Final Answer: The value of p is 600.
Did you try all the features and get comfortable using them? You should work on using the Desmos calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must attempt as many questions as you can before the final test. This is the 2nd Practice Test of SAT Math Module 2nd.
Either you can take the 3rd Practice Test of SAT Math or the 3rd Practice Test of SAT Reading and Writing Module 2nd.
- SAT Test 3rd (Math Module 2nd)
- SAT Test 2nd (Math Module 1st)
- SAT Test 3rd (Reading and Writing Module 2nd)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


