
SAT MATH TEST: SOLUTIONS AND EXPLANATIONS
Have you taken the module 1st? If yes, then you are in the right place. This is the 6th Test of Module 2nd. We have designed a similar exam format with all the necessary features for you to become a master in Math. You take the SAT Test Module Second to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 2nd.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 2ND
The second module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 2nd are only difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 2nd. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH STUDY GUIDE AND PROBLEM SOLUTIONS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: Tilly earns p dollars for every w hours of work. Which expression represents the amount of money, in dollars, Tilly earns for 39w hours of work?
A) 39p
B) p/39
C) p + 39
D) p – 39
Choice A is correct. It’s given that Tilly earns p dollars for every w hours of work. This can be represented by the proportion p/w. The amount of money, x, Tilly earns for 39w hours of work can be found by setting up the proportion p/w = x/39. This can be rewritten as 39pw = xw. Dividing both sides by w results in x = 39p.
Choice B is incorrect. This is the amount of money Tilly earns in dollars per hour, not the amount of money Tilly earns for 39w hours of work.
Choice C is incorrect. This is the amount of money Tilly earns for w hours of work plus 39, not the amount of money Tilly earns for 39w hours of work.
Choice D is incorrect. This is the amount of money Tilly earns for w hours of work minus 39, not the amount of money Tilly earns for 39w hours of work.
Problem Breakdown
We are tasked with determining the amount of money, in dollars, that Tilly earns for 39w hours of work given the relationship that Tilly earns p dollars for every w hours of work.
Step-by-Step Solution:
1. Understand the relationship:
From the problem, Tilly earns p dollars for every w hours of work. This establishes a proportional relationship between her earnings and her working hours:
Earnings per hour = p/w
This means for every 1 hour of work, Tilly earns p/w dollars.
2. Use proportional reasoning:
If Tilly works 39w hours, we can calculate her total earnings by multiplying her hourly earnings by the total hours she works:
Total earnings = Earnings per hour × Total hours
Substitute the known values:
Total earnings = p/w × 39w
3. Simplify the expression:
In the expression p/w × 39w, the w in the numerator and denominator cancels out:
Total earnings = 39p
Thus, the amount of money Tilly earns for 39w hours of work is 39p dollars.
4. Verify the expression with an example:
Let’s verify the result by using specific numbers for p and w:
~ Suppose p = 100 dollars and w = 5 hours. This means Tilly earns 100 dollars for every 5 hours.
~ For 39w = 39(5) = 195 hours:
~ ~ Hourly earnings = p/w = 100/5 = 20 dollars per hour.
~ ~ Total earnings = 20 × 195 = 3900 dollars.
~ ~ Using the formula 39p = 39 × 100 = 3900, we get the same result.
The formula 39p is verified.
Final Answer: A) 39p.
2nd Question
Question: For a training program, Juan rides his bike at an average rate of 5.7 minutes per mile. Which function m models the number of minutes it will take Juan to ride x miles at this rate?
A) m(x) = x/5.7
B) m(x) = x + 5.7
C) m(x) = x – 5.7
D) m(x) = 5.7x
Choice D is correct. It′s given that Juan rides his bike at an average rate of 5.7 minutes per mile. The number of minutes it will take Juan to ride x miles can be determined by multiplying his average rate by the number of miles, x, which yields 5.7x. Therefore, the function m(x) = 5.7x models the number of minutes it will take Juan to ride x miles.
Choice A is incorrect and may result from conceptual errors.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Problem Breakdown
We need to determine the function m(x) that models the number of minutes m it will take Juan to ride x miles, given that Juan rides his bike at an average rate of 5.7 minutes per mile.
Step-by-Step Solution:
1. Understand the given rate:
The problem states that Juan rides 1 mile in 5.7 minutes. This means for each mile he rides, the time required increases by 5.7 minutes.
This establishes a proportional relationship:
Total time (minutes) (Rate of time per mile) × (Total distance in miles)
In mathematical terms:
m(x) = 5.7 ⋅ x
2. Analyze each option:
Option A: m(x) = x/5.7
~ This equation implies that the number of minutes decreases as x increases, which is incorrect because Juan takes more time as he rides more miles.
~ Therefore, this option is incorrect.
Option B: m(x) = x + 5.7
~ This equation implies that Juan takes x minutes plus an additional fixed 5.7 minutes, regardless of how far he rides.
~ This is inconsistent with the given rate, as the total time is directly proportional to x.
Therefore, this option is incorrect.
Option C: m(x) = x − 5.7
This equation suggests that Juan’s total time decreases by 5.7 minutes as he rides more miles, which is nonsensical in this context.
Therefore, this option is incorrect.
Option D: m(x) = 5.7x
This equation correctly models the relationship between x (miles) and m(x) (minutes). For every mile, Juan takes an additional 5.7 minutes, so the total time is proportional to the number of miles ridden.
Therefore, this option is correct.
3. Verify with an example:
Suppose Juan rides 3 miles (x = 3):
~ Using the given rate: 5.7 minutes per mile, the total time is:
m(x) = 5.7 ⋅ 3 = 17.1 minutes.
~ Using Option D (m(x) = 5.7x):
m(3) = 5.7 ⋅ 3 = 17.1 minutes.
This matches the expected result, verifying that m(x) = 5.7x is correct.
Final Answer: D) m(x) = 5.7x.
3rd Question
3x = 12
-3x + y = -6
Question: The solution to the given system of equations is (x, y). What is the value of y?
A) −3
B) 6
C) 18
D) 30
Choice B is correct. Adding the second equation in the given system to the first equation in the given system yields 3x + (-3x + y) = 12 + (-6), which is equivalent to y = 6.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown
We are tasked with solving the system of equations:
1) 3x = 12
2) −3x + y = −6
We need to find the values of x and y, and specifically determine the value of y. This involves solving the system step by step.
Step-by-Step Solution:
Step 1: Solve for x in the first equation
The first equation is:
3x = 12
To isolate x, divide both sides by 3:
x = 12/3 = 4
Thus, x = 4.
Step 2: Substitute x = 4 into the second equation
The second equation is:
−3x + y = −6
Substitute x = 4 into this equation:
−3(4) + y = −6
Simplify: −12 + y = −6
Step 3: Solve for y
To isolate y, add 12 to both sides:
y = −6 + 12
y = 6
Thus, y = 6.
Verify the Solution
To ensure the solution is correct, substitute x = 4 and y = 6 into both original equations:
1) First equation: 3x = 12
Substitute x = 4:
3(4) = 12 (True).
2) Second equation:
−3x + y = −6
Substitute x = 4 and y = 6:
−3(4) + 6 = −6
−12 + 6 = −6(True).
Both equations are satisfied, confirming that the solution is correct.
Final Answer: The solution to the system is (x, y) = (4, 6), so the value of y is: B) 6.
4th Question
s = 40 + 3t
Question: The equation gives the speed s, in miles per hour, of a certain car t seconds after it began to accelerate. What is the speed, in miles per hour, of the car 5 seconds after it began to accelerate?
A) 40
B) 43
C) 45
D) 55
Choice D is correct. In the given equation, s is the speed, in miles per hour, of a certain car t seconds after it began to accelerate. Therefore, the speed of the car, in miles per hour, 5 seconds after it began to accelerate can be found by substituting 5 for t in the given equation, which yields s = 40 + 3(5), or s = 55. Thus, the speed of the car 5 seconds after it began to accelerate is 55 miles per hour.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
The given equation is:
s = 40 + 3t
This equation describes the speed s (in miles per hour) of a car t seconds after it began accelerating. We are tasked with finding the speed of the car 5 seconds after it began to accelerate.
To solve this, substitute t = 5 into the equation and calculate the value of s.
Step-by-Step Solution:
Step 1: Understand the problem
The equation s = 40 + 3t tells us that the car’s speed starts at 40 mph (when t = 0), and it increases by 3 mph for every second of acceleration (3t).
We need to find the speed of the car when t = 5.
Step 2: Substitute t = 5 into the equation
s = 40 + 3t
Substitute t = 5:
s = 40 + 3(5)
Step 3: Simplify the equation
s = 40 + 15
s = 55
Verification:
To verify, we check the logic:
~ At t = 0, the speed is s = 40 + 3(0) = 40, which matches the initial speed.
~ After 5 seconds, the speed increases by 3 × 5 = 15, giving a total speed of 40 + 15 = 55, which is consistent.
The calculation is correct.
Final Answer: The speed of the car 5 seconds after it began to accelerate is: D) 55 mph.
5th Question
Question:
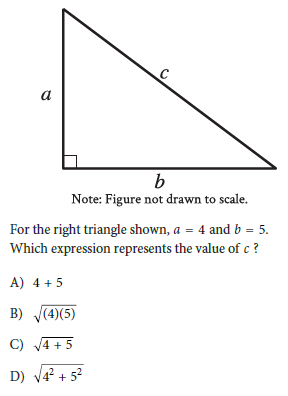
Choice D:

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Statement:
We are given a right triangle with legs a = 4 and b = 5. We are tasked with determining the expression that represents the hypotenuse c using the Pythagorean theorem.
Step 1: Recall the Pythagorean Theorem
For a right triangle, the Pythagorean theorem states:
c2 = a2 + b2,
where c is the hypotenuse, and a and b are the two legs of the triangle.
Step 2: Substitute the given values
Substituting a = 4 and b = 5 into the formula:
c2 = 42 + 52.
Simplify:
c2 = 16 + 25.
Add the values:
c2 = 41.
Step 3: Solve for c
To find c, take the square root of both sides:

Final Answer: Option D.
How Do We Know It Is Pythagorean?
The problem explicitly states that we are dealing with a right triangle. The Pythagorean theorem only applies to right triangles, so it’s the logical choice here. (The term “right” here doesn’t mean “direction”; it refers to the angle being exactly 90°.)
~ In a right triangle, one angle is exactly 90°.
~ The hypotenuse is the longest side, opposite the right angle.
~ The theorem is a universal rule that helps relate the three sides of any right triangle.
Since we’re given a right triangle and are asked to find the hypotenuse, the Pythagorean theorem is the appropriate tool.
What Is the Pythagorean Theorem?
The Pythagorean theorem is a mathematical rule that states:
c2 = a2 + b2
Where:
~ c is the length of the hypotenuse (the side opposite the right angle),
~ a and b are the lengths of the two legs of the triangle.
This formula works because, in a right triangle, the sum of the areas of the squares on the two legs equals the area of the square on the hypotenuse. (What is Hypotenuse?: The longest side of a right triangle. )
Why Is Squaring Important in the Theorem?
Squaring ensures that all sides contribute positively to the relationship, regardless of their direction. This is because:
~ Squaring eliminates negative signs (since distance cannot be negative).
~ It reflects the geometric principle behind the theorem, which is based on areas.
By squaring the sides, we ensure that the lengths are treated as components of a consistent mathematical relationship.
6th Question
Question: If 6n = 12, what is the value of n + 4?
A) -6
B) 6
C) 2
D) -2
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 6. Dividing both sides of the equation 6n = 12 by 6 yields n = 2. Substituting 2 for n in the expression n + 4 yields 2 + 4, or 6.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Solve for n
The equation 6n = 12 means that 6 times n equals 12. To isolate n, divide both sides of the equation by 6:
6n ÷ 6
= 12 ÷ 6
n = 2
Step 2: Find n + 4
Now that we know n = 2, substitute nnn into the expression n + 4:
n + 4
= 2 + 4
n + 4 = 6
Verification:
To verify the solution:
1) Check the solution for n:
If 6n = 12, substituting n = 2 gives:
6(2) = 12
This is correct.
2) Substituting n = 2 into n + 4 gives:
n + 4
= 2 + 4
= 6
This is consistent with the solution.
Final Answer: The value of n + 4 is: B) 6.
7th Question
(d − 30)(d + 30) − 7 = −7
Question: What is a solution to the given equation?
A) −30
B) −7
C) 0
D) 37
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is either -30 or 30. Adding 7 to each side of the given equation yields (d – 30)(d + 30) = 0. Since a product of two factors is equal to 0 if and only if at least one of the factors is 0, either d – 30 = 0 or d + 30 = 0. Adding 30 to each side of the equation d – 30 = 0 yields d = 30. Subtracting 30 from each side of the equation d + 30 = 0 yields d = -30. Therefore, the solutions to the given equation are -30 and 30. Note that -30 and 30 are examples of ways to enter a correct answer. Based on option, -30 is correct.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:

Verification:
1) Substitute d = 30 into the original equation:
(30 − 30)(30 + 30) − 7 = −7
(0)(60) − 7 = −7
−7 = −7 (True).
2) Substitute d = −30 into the original equation:
(−30 − 30)(−30 + 30) − 7 = −7
(−60)(0) − 7 = −7
−7 = −7 (True).
Both solutions are correct. But based on given options -30.
Final Answer: A) -30.
8th Question
Question: Line r in the xy-plane has a slope of 4 and passes through the point (0, 6). Which equation defines line r?
A) y = −6x + 4
B) y = 6x + 4
C) y = 4x − 6
D) y = 4x + 6
Choice D is correct. A line in the xy-plane with a slope of m and a y-intercept of (0, b) can be defined by an equation in the form y = mx + b. It’s given that line r has a slope of 4 and passes through the point (0, 6). It follows that m = 4 and b = 6. Substituting 4 for m and 6 for b in the equation y = mx + b yields y = 4x + 6. Therefore, the equation y = 4x + 6 defines line r.
Choice A is incorrect. This equation defines a line that has a slope of -6, not 4, and passes through the point (0, 4), not (0, 6).
Choice B is incorrect. This equation defines a line that has a slope of 6, not 4, and passes through the point (0, 4), not (0, 6).
Choice C is incorrect. This equation defines a line that passes through the point (0,-6), not (0, 6).
Problem Breakdown:
We need to determine the equation of a line with the following characteristics:
1) Slope: m = 4
2) Point: Passes through (0, 6).
Step-by-Step Solution:
Step 1: Use the Slope-Intercept Form
The slope-intercept form of a line is:
y = mx + b
Here, m is the slope, and b is the y-intercept (the y-coordinate where the line crosses the y-axis).
Step 2: Identify the Y-Intercept
The line passes through the point (0, 6). Since the x-coordinate is 0, the y-coordinate (6) is the y-intercept. Thus:
b = 6
Step 3: Substitute m and b
The slope m = 4 and the y-intercept b = 6. Substituting these values into the slope-intercept form:
y = 4x + 6
Verification
To ensure the equation is correct:
~ The slope is 4, as given.
~ The line passes through (0, 6): Substituting x = 0 into y = 4x + 6,
y = 4(0) + 6
y = 6
This confirms the point (0, 6) lies on the line.
Final Answer: The equation defining the line is: D) y = 4x + 6.
9th Question
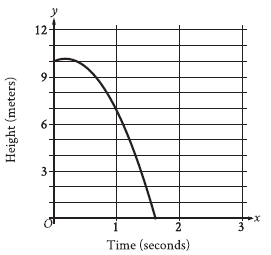
Question: A competitive diver dives from a platform into the water. The graph shown gives the height above the water y, in meters, of the diver x seconds after diving from the platform. What is the best interpretation of the x-intercept of the graph?
A) The diver reaches a maximum height above the water at 1.6 seconds.
B) The diver hits the water at 1.6 seconds.
C) The diver reaches a maximum height above the water at 0.2 seconds.
D) The diver hits the water at 0.2 seconds.
Choice B is correct. It’s given that the graph shows the height above the water y, in meters, of a diver x seconds after diving from a platform. The x-intercept of a graph is the point at which the graph intersects the x-axis, or when the value of y is 0. The graph shown intersects the x-axis between x = 1 and x = 2. In other words, the diver is 0 meters above the water, or hits the water, between 1 and 2
seconds after diving from the platform. Of the given choices, only choice B includes an interpretation where the diver hits the water between 1 and 2 seconds. Therefore, the best interpretation of the x-intercept of the graph is the diver hits the water at 1.6 seconds.
Choice A is incorrect and may result from conceptual errors.
Choice C is incorrect. This is the best interpretation of the maximum value, not the x-intercept, of the graph.
Choice D is incorrect and may result from conceptual errors.
Step-by-Step Explanation
To solve the question, let’s analyze the situation in depth using the provided graph and the concept of x-intercepts:
1. Understand What the x-Intercept Represents
~ The x-intercept is the point where the graph crosses the x-axis.
~ At this point, the value of y, which represents the height above the water, equals 0.
~ In this context, y = 0 means the diver has reached the surface of the water.
2. Determine the x-Intercept
~ Look at the graph. The x-axis is labeled “Time (seconds),” and the x-intercept is at x = 1.6.
~ Therefore, at x = 1.6 seconds, the height y of the diver is 0, meaning the diver hits the water at this point.
3. Evaluate Each Answer Choice
Let’s review each option carefully:
A) The diver reaches a maximum height above the water at 1.6 seconds.
~ This is incorrect because the maximum height occurs at the highest point of the curve, not at the x-intercept.
~ The highest point appears to be approximately x = 0.5 seconds, where y ≈ 10 meters.
B) The diver hits the water at 1.6 seconds.
~ This is correct because the diver’s height above water (y) becomes 0 at x = 1.6, as determined by the x-intercept.
C) The diver reaches a maximum height above the water at 0.2 seconds.
~ This is incorrect because the diver’s maximum height is at approximately x = 0.5 seconds, not at x = 0.2.
D) The diver hits the water at 0.2 seconds.
~ This is incorrect because the diver hits the water at x = 1.6, not at x = 0.2.
4. Verify the Correct Answer
~ From the graph and the reasoning above, the x-intercept corresponds to the time when the diver reaches the water’s surface. This happens at x = 1.6 seconds.
~ Thus, the correct answer is: B) The diver hits the water at 1.6 seconds.
10th Question
Question: The kinetic energy, in joules, of an object with mass 9 kilograms traveling at a speed of v meters per second is given by the function K, where K(v) = 9/2 v2. Which of the following is the best interpretation of K(34) = 5,202 in this context?
A) The object traveling at 34 meters per second has a kinetic energy of 5,202 joules.
B) The object traveling at 340 meters per second has a kinetic energy of 5,202 joules.
C) The object traveling at 5,202 meters per second has a kinetic energy of 34 joules.
D) The object traveling at 23,409 meters per second has a kinetic energy of 34 joules.
Choice A is correct. It’s given that the kinetic energy, in joules, of an object with a mass of 9 kilograms traveling at a speed of v meters per second is given by the function K, where K(v) = 9/2 v2. It follows that in the equation K(34) = 5,202, 34 is the value of v, or the speed of the object, in meters per second, and 5,202 is the kinetic energy, in joules, of the object at that speed. Therefore, the best interpretation of K(34) = 5,202 in this context is the object traveling at 34 meters per second has a kinetic energy of 5,202 joules.
Choice B is incorrect. The object traveling at 340 meters per second has a kinetic energy of 520,200 joules.
Choice C is incorrect. The object traveling at 5,202 meters per second has a kinetic energy of 121,773,618 joules.
Choice D is incorrect. The object traveling at 23,409 meters per second has a kinetic energy of 2,465,915,764.5 joules.
Problem Breakdown:
We are given the kinetic energy function for an object:
K(v) = 9/2 v2
Where:
~ K(v) is the kinetic energy in joules,
~ v is the speed of the object in meters per second.
We are asked to interpret K(34) = 5,202.

Step 3: Interpret the Answer Choices
Choice A: “The object traveling at 34 meters per second has a kinetic energy of 5,202 joules.”
~ This matches the result we calculated and is correct.
Choice B: “The object traveling at 340 meters per second has a kinetic energy of 5,202 joules.”
~ Incorrect: The speed is 34, not 340.
Choice C: “The object traveling at 5,202 meters per second has a kinetic energy of 34 joules.”
~ Incorrect: The interpretation reverses K(v) and v.
Choice D: “The object traveling at 23,409 meters per second has a kinetic energy of 34 joules.”
~ Incorrect: There’s no basis for this interpretation in the context.
Final Answer:
A) The object traveling at 34 meters per second has a kinetic energy of 5,202 joules.
11th Question
Question: A circle has a center O, and points R and S lie on the circle. In triangle ORS, the measure of ∠ROS is 88°. What is the measure of ∠RSO, in degrees?
A) 188°
B) 92°
C) 88°
D) 46°
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 46. It’s given that O is the center of a circle and that points R and S lie on the circle. Therefore, ‘OR and OS‘ are radii of the circle. It follows that OR = OS. If two sides of a triangle are congruent, then the angles opposite them are congruent. It follows that the angles ∠RSO and ∠ORS, which are across from the sides of equal length, are congruent. Let x° represent the measure of ∠RSO. It follows that the measure of ∠ORS is also x°. It’s given that the measure of ∠ROS is 88°. Because the sum of the measures of the interior angles of a triangle is 180°, the equation x° + x° + 88° = 180°, or 2x + 88 = 180, can be used to find the measure of ∠RSO. Subtracting 88 from both sides of this equation yields 2x = 92. Dividing both sides of this equation by 2 yields x = 46. Therefore, the measure of ∠RSO, in degrees, is 46.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
We are given:
~ A circle with center O,
~ Points R and S lying on the circle,
~ In △ORS, the angle at the center (∠ROS) is 88°,
~ We are tasked with finding the measure of ∠RSO, which is one of the base angles of △ORS.
Step-by-Step Solution:
Step 1: Understand the Geometry
~ Since R and S lie on the circle and O is the center:
~ ~ OR and OS are radii of the circle.
~ ~ △ORS is an isosceles triangle, because two sides (OR and OS) are equal in length.
~ The property of an isosceles triangle tells us:
~ ~ The two base angles, ∠RSO and ∠SRO, are equal.
Step 2: Use the Triangle Sum Theorem
The sum of the angles in a triangle is always 180°. In △ORS, this gives:
∠ROS + ∠RSO + ∠SRO = 180°
Substituting ∠ROS = 88°:
88° + 2∠RSO = 180°
Step 3: Solve for ∠RSO
1) Subtract 88° from both sides: 2∠RSO = 92°
2) Divide by 2: ∠RSO = 46°
Verification:
In △ORS, the angles are:
~ ∠ROS = 88°,
~ ∠RSO = 46°,
~ ∠SRO = 46° (because it’s isosceles).
Adding these: 88° + 46° + 46° = 180°
This confirms our solution.
Final Answer: The measure of ∠RSO is: D) 46°.
12th Question
x(x + 1) – 56 = 4x(x – 7)
Question: What is the sum of the solutions to the given equation?
A) 6.667
B) 7.667
C) 8.667
D) 9.667
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
We are tasked with finding the sum of the solutions to the equation:
x(x + 1) − 56 = 4x(x − 7)
This involves solving a quadratic equation and using properties of polynomials to find the sum of the solutions.
Step-by-Step Solution:
Step 1: Expand and Simplify Both Sides
1) Expand the left-hand side [x(x + 1) − 56]:
x2 + x − 56
2) Expand the right-hand side [4x(x − 7)]:
4x2 − 28x
The equation becomes: x2 + x − 56 = 4x2 − 28x
Step 2: Rearrange into Standard Form
Bring all terms to one side of the equation so the right-hand side is 0:
x2 + x − 56 − 4x2 + 28x = 0
Combine like terms: −3x2 + 29x − 56 = 0
Step 3: Factor Out −1
It’s easier to work with a positive leading coefficient, so factor out −1:
3x2 − 29x + 56 = 0
Step 4: Use the Relationship Between Roots and Coefficients
The quadratic equation is now:
3x2 − 29x + 56 = 0
For a quadratic equation in the form ax2 + bx + c = 0, the sum of the solutions is given by:
Sum of solutions = −b/a
Here:
~ a = 3 (coefficient of x2),
~ b = −29 (coefficient of x).
Substitute these values:
Sum of solutions = – (−29/3)
= 29/3
= 9.666
= 9.667.

Final Answer: D) 9.667.
Why Use −b/a Here?
The formula −b/a is a property of quadratic equations that comes from their fundamental nature. In any quadratic equation of the form:
ax2 + bx + c = 0,
the sum of the solutions (x1 and x2) is always given by:
x1 + x2 = −b/a.
This comes from the relationship between the roots and coefficients of a quadratic equation. Specifically:
~ The sum of the solutions is −b/a,
~ The product of the solutions is c/a.
This is derived from the factored form of a quadratic equation:
ax2 + bx + c = a(x − x1)(x − x2).
Since the question explicitly asks for the sum of the solutions, and this property allows us to find the sum directly without solving for the individual solutions, using −b/a is the most efficient method.
When to Use Other Methods
1) Factoring Method:
~ Use factoring when the quadratic equation can be written as a product of two binomials:
(x − x1)(x − x2) = 0.
~ Factoring is typically preferred when the coefficients are simple and the solutions are integers or easy-to-guess rational numbers.
~ For example, for x2 − 5x + 6 = 0, we can easily factor it as:
(x − 2)(x − 3) = 0.
2) Quadratic Formula:
~ Use the quadratic formula when the quadratic equation cannot be factored easily, or when the solutions might involve irrational numbers or decimals: (See the Verification)
In this case, solving 3x2 − 29x + 56 = 0 using the quadratic formula would work too, but it requires more steps compared to directly using the −b/a property.
Why I Chose −b/a in This Problem
The question asks only for the sum of the solutions, not the individual solutions. Since the sum of the solutions is directly related to the coefficients of the quadratic equation, it is quicker and more efficient to use −b/a than to solve for x1 and x2 explicitly.
13th Question
y = 3x
2x + y = 12
Question: The solution to the given system of equations is (x, y). What is the value of 5x?
A) 24
B) 15
C) 12
D) 5
Choice C is correct. It’s given by the first equation in the system that y = 3x. Substituting 3x for y in the equation 2x + y = 12 yields 2x + 3x = 12, or 5x = 12.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Substitution
Since y = 3x is already expressed in terms of x, we can substitute y = 3x into the second equation 2x + y = 12.
Substituting:
2x + y = 12
2x + 3x = 12
Step 2: Simplify the Equation
Simplify the left-hand side:
5x = 12
Step 3: Solve for x
Divide both sides of the equation by 5 to isolate x:
x = 12/5
Step 4: Find 5x
We are asked to find 5x, not just x. Since 5x = 12, the solution is:
5x = 12
Verification
Let’s verify the solution by substituting x = 12/5 into both original equations.
1) From y = 3x:
y = 3(12/5) = 36/5.
2) Substitute x = 12/5 and y = 36/5 into 2x + y = 12:
2(12/5) + 36/5
= 24/5 + 36/5
= 60/5
= 12.
This satisfies the second equation.
Thus, the solution is correct.
Final Answer: C) 12.
14th Question
Question: Five Eretmochelys imbricata, a type of sea turtle, each have a nest. The table shows an original data set of the number of eggs that each turtle laid in its nest.
| Nest | Number of Eggs |
|---|---|
| A | 149 |
| B | 144 |
| C | 148 |
| D | 136 |
| E | 139 |
A sixth nest with 121 eggs is added to create a new data set. Which of the following correctly compares the means of the two data sets?
A) The mean of the original data set is greater than the mean of the new data set.
B) The mean of the original data set is less than the mean of the new data set.
C) The means of both data sets are equal.
D) There is not enough information to compare the means.
Choice A is correct. It’s given that the table shows an original data set of 5 values. It’s also given that a sixth value is added to create a new data set. The new data set consists of the 5 values in the original data set and one additional value, 121. Since the additional value, 121, is less than any value in the original data set, the mean of the original data set is greater than the mean of the new data set.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation
This question asks us to compare the means of two data sets—(1) the original data set of the number of eggs laid in five nests and (2) the new data set, which includes an additional nest with 121 eggs.

Step 5: Analyze the Answer Choices
A) The mean of the original data set is greater than the mean of the new data set.
~ This is correct because 143.2 > 139.5.
B) The mean of the original data set is less than the mean of the new data set.
~ This is incorrect because 143.2 is greater, not less.
C) The means of both data sets are equal.
~ This is incorrect because the two means are different.
D) There is not enough information to compare the means.
~ This is incorrect because we have enough information (the number of eggs and nests) to calculate the means.
The correct answer is: A) The mean of the original data set is greater than the mean of the new data set.
Verification
Let’s double-check by redoing the sums:
~ Sum of the original data: 149 + 144 + 148 + 136 + 139 = 716
~ Sum of the new data: 716 + 121 = 837
~ Means:
~ ~ Original: 716/5 = 143.2
~ ~ New: 837/6 = 139.5 Both calculations match, so the answer is verified.
Final Answer: Option A.
15th Question
Question: In △RST, the measure of ∠R is 63°. Which of the following could be the measure, in degrees, of ∠S?
A) 116
B) 118
C) 126
D) 180
Choice A is correct. The sum of the measures of the angles of a triangle is 180°. Therefore, the sum of the measures of ∠R, ∠S, and ∠T is 180°. It’s given that the measure of ∠R is 63°. It follows that the sum of the measures of ∠S and ∠T is (180 – 63)°, or 117°. Therefore, the measure of ∠S, in degrees, must be less than Of the given choices, only 116 is less than 117. Thus, the measure, in degrees, of ∠S could be 116.
Choice B is incorrect. If the measure of ∠S is 118°, then the sum of the measures of the angles of the triangle is greater than, not equal to, 180°.
Choice C is incorrect. If the measure of ∠S is 126°, then the sum of the measures of the angles of the triangle is greater than, not equal to, 180°.
Choice D is incorrect. This is the sum of the measures of the angles of a triangle, in degrees.
Step-by-Step Explanation
This question is about angles in a triangle, specifically in △RST. To solve it, we need to recall the basic properties of triangles.
Step 1: Understand the Triangle Sum Theorem
The Triangle Sum Theorem states:
The sum of the angles in a triangle is always 180°.
For △RST, this means:
∠R + ∠S + ∠T = 180°.
We are given:
∠R = 63°,
and we need to determine the possible value of ∠S.
Let’s express ∠T in terms of the other two angles:
∠T = 180° − (∠R + ∠S).
Step 2: Identify the Range for ∠S
In any triangle:
1) Each angle must be greater than 0°.
2) Each angle must be less than 180°.
3) The sum of any two angles must be less than 180°.
With ∠R = 63°, the sum of ∠S and ∠T is:
∠S + ∠T = 180° − 63° = 117°.
This means:
∠S + ∠T = 117°, and both ∠S and ∠T must be less than 117°.
Thus, ∠S must satisfy the following conditions:
1) 0° < ∠S < 117°.
2) The value ∠S is between 0 and 117, so based on the options. It is 116.
Step 3: Verify the Possibility of ∠S
Since ∠S must be between 0° and 117°, there are many possible values for ∠S.
~ For example, if ∠S = 50°, then:
∠T = 180° − (63° + 50°) = 67°.
This is valid because all three angles are positive and their sum is 180°.
~ Similarly, if ∠S = 30°, then:
∠T = 180° − (63° + 30°) = 87°.
This is also valid.
As long as ∠S satisfies 0° < ∠S < 117°, it is a valid measure.
Final Answer: A) 116.
16th Question
Question: Which expression is equivalent to (8x3 + 8) − (x3 − 2)?
A) 8x3 + 6
B) 7x3 + 10
C) 8x3 + 10
D) 7x3 + 6
Choice B is correct. The given expression is equivalent to 8x3 + 8 – x3 – (-2), or 8x3 + 8 – x3 + 2. Combining like terms in this expression yields 7x3 + 10.
Choice A is incorrect. This expression is equivalent to (8x3 + 8) – 2, not (8x3 + 8) – (x3 – 2).
Choice C is incorrect. This expression is equivalent to (8x3 + 8) – (-2), not (8x3 + 8) – (x3 – 2).
Choice D is incorrect. This expression is equivalent to (8x3 + 8) – (x3 + 2), not (8x3 + 8) – (x3 – 2).
Step-by-Step Explanation
We are tasked with simplifying the given expression and determining which option matches the result. Here’s the process broken down in detail:
Step 1: Write Down the Expression
The given expression is:
(8x3 + 8) − (x3 − 2).
Step 2: Distribute the Negative Sign
When subtracting a group of terms inside parentheses, distribute the negative sign to all terms inside the second set of parentheses
(8x3 + 8) − (x3 − 2) = 8x3 + 8 − x3 + 2.
Step 3: Combine Like Terms
Now, group the terms with x3 together and the constant terms together:
(8x3 − x3) + (8 + 2).
Simplify:
8x3 − x3 = 7x3,
8 + 2 =10.
Thus, the simplified expression is:
7x3 + 10.
Step 4: Match the Simplified Expression
The simplified expression 7x3 + 10 corresponds to Option B.
Step 5: Verify the Simplification
Let’s verify by substituting a value for x into the original expression and our simplified expression to ensure they are equivalent.
1) Substitute x = 1 into the original expression:
[8(1)3 + 8] − [(1)3 − 2)
= (8 + 8) − (1 − 2)
= 16 − (−1)
= 16 + 1 = 17.
2) Substitute x = 1 into the simplified expression 7x3 + 10:
7(1)3 + 10 = 7 + 10 = 17.
Both calculations yield the same result (17), confirming the simplification is correct.
Final Answer: Option B.
17th Question
Question:
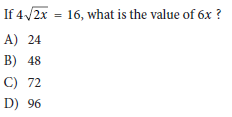
Choice B is correct. Dividing each side of the given equation by 4 yields ‘square root of 2x‘ = 4. Squaring both sides of this equation yields 2x = 16. Multiplying each side of this equation by 3 yields 6x = 48. Therefore, the value of 6x is 48.
Choice A is incorrect. This is the value of 3x, not 6x.
Choice C is incorrect. This is the value of 9x, not 6x.
Choice D is incorrect. This is the value of 12x, not 6x.
Step-by-Step Solution
1. Write the given equation:
Use the first equation to find the value of x for the value of 6x.
2. Isolate the Square Root Term
Divide both sides of the equation by 4 to simplify:

The original equation is satisfied, confirming the solution is correct.
Final Answer: B) 48.
18th Question
–x2 + bx – 676 = 0
Question: In the given equation, b is a positive integer. The equation has no real solution. What is the greatest possible value of b?
A) 51
B) 52
C) 676
D) 2704
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 51. A quadratic equation of the form ax2 + bx + c = 0, where a, b, and c are constants, has no real solution if and only if its discriminant, -4ac + b2, is negative. In the given equation, a = -1 and c = -676. Substituting -1 for a and -676 for c in this expression yields a discriminant of b2 – 4(-1)(-676), or b2 – 2,704. Since this value must be negative, b2 – 2,704 < 0, or b2 < 2,704. Taking the positive square root of each side of this inequality yields b < 52. Since b is a positive integer, and the greatest integer less than 52 is 51, the greatest possible value of b is 51.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation
We are tasked with finding the greatest possible value of b in the quadratic equation:
−x2 + bx − 676 = 0
such that the equation has no real solution.
Step 1: Identify the Condition for No Real Solution
The discriminant (Δ) of a quadratic equation determines the nature of its solutions:
Δ = b2 − 4ac,
where a, b, and c are the coefficients of the quadratic equation ax2 + bx + c = 0.
1) If Δ > 0, the equation has two real and distinct solutions.
2) If Δ = 0, the equation has exactly one real solution.
3) If Δ < 0, the equation has no real solutions.
We need to ensure that: Δ < 0.
Step 2: Write the Coefficients
Rearrange the given equation to standard quadratic form ax2 + bx + c = 0:
−x2 + bx − 676 = 0.
Here:
a = −1, b = b, c = −676.
Step 3: Substitute into the Discriminant Formula
Substitute the values of a, b, and c into the discriminant formula:
Δ = b2 − 4ac.
Since a = −1 and c = −676, we have:
Δ = b2 − 4(−1)(−676).
Simplify:
Δ = b2 − 4(676),
Δ = b2 − 2704.
Step 4: Ensure Δ < 0
For the equation to have no real solutions:
b2 − 2704 < 0.
Rearrange: b2 < 2704.
Step 5: Solve for b
Take the square root of both sides:
b < square root of 2704.
Simplify the square root of 2704 is: 52.
Thus: b < 52.
Since b must be a positive integer, the greatest possible value of b is:
b = 51.
Step 6: Verify the Solution
Substitute b = 51 into the discriminant formula to confirm that Δ < 0:
1) Calculate Δ:
Δ = b2 − 2704
Δ = 512 − 2704.
Δ = 2601 − 2704
Δ = −103.
Since Δ < 0, the equation has no real solution for b = 51.
2) Check b = 52:
Δ = b2 − 2704
Δ = 522 − 2704
Δ = 2704 − 2704
Δ = 0.
Since Δ = 0, the equation has one real solution for b = 52, so b = 52 is invalid.
Thus, the greatest possible value of b is indeed 51.
Final Answer: A) 51.
19th Question
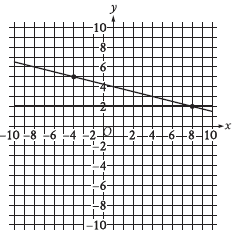
Question: If a new graph of three linear equations is created using the system of equations shown and the equation x + 4y = −16, how many solutions (x, y) will the resulting system of three equations have?
A) Zero
B) Exactly one
C) Exactly two
D) Infinitely many
Choice A is correct. A solution to a system of equations must satisfy each equation in the system. It follows that if an ordered pair (x, y) is a solution to the system, the point (x, y) lies on the graph in the xy-plane of each equation in the system. The only point that lies on each graph of the system of two linear equations shown is their intersection point (8, 2). It follows that if a new graph of three linear equations is created using the system of equations shown and the graph of x + 4y = -16, this system has either zero solutions or one solution, the point (8, 2). Substituting 8 for x and 2 for y in the equation x + 4y = -16 yields 8 + 4(2) = -16, or 16 = -16. Since this equation is not true, the point (8, 2) does not lie on the graph of x + 4y = -16. Therefore, (8, 2) is not a solution to the system of three equations. It follows that there are zero solutions to this system.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Problem
We are analyzing a system of three linear equations:
1) The two equations represented by the lines in the graph.
~ (x, y) = (8, 2)
~ (x, y) = (-4, 5)
2) The third equation: x + 4y = −16.
We need to determine how many solutions this system has. A solution to the system is a point (x, y) that satisfies all three equations simultaneously.
Step 2: Key Facts About the Graph
From the graph:
~ The two lines shown intersect at exactly one point, which is (8, 2).
~ This means that (8, 2) is the only solution to the system of the two equations already graphed.
Step 3: Adding the Third Equation
The third equation is:
x + 4y = −16
Let’s check whether the point of intersection (8, 2), which satisfies the first two equations, also satisfies this equation.
Step 4: Substitute (8, 2) into x + 4y = −16
Substitute x = 8 and y = 2 into x + 4y = −16:
8 + 4(2)
= 8 + 8 = 16
The left-hand side is 16, but the equation says it must equal −16.
16 ≠ −16
This means that (8, 2) does not satisfy the equation x + 4y = −16.
Step 5: Interpret the Result
Since the point (8, 2) does not satisfy x + 4y = −16, the three lines do not intersect at a common point. Therefore, there is no point in the xy-plane that satisfies all three equations simultaneously.
Step 6: Verification
Substitute x = -4 and y = 5 into x + 4y = −16:
-4 + 4(5) = -16
-4 + 20 = -16
16 ≠ −16
The left-hand side is 16, but the equation says it must equal −16.
That means there is Zero solutions.
Step 7: Conclusion
The system of three equations has no solutions, because there is no single point that lies on all three graphs.
Final Answer: A) Zero.
20th Question
f(x) = 5,470(0.64)x/12
Question: The function f gives the value, in dollars, of a certain piece of equipment after x months of use. If the value of the equipment decreases each year by p% of its value the preceding year, what is the value of p?
A) 4
B) 5
C) 36
D) 64
Choice C is correct. For a function of the form f(x) = a(r)x/k , where a, r, and k are constants and r < 1, the value of f(x) decreases by 100(1 – r)% for every increase of x by k. In the given function, a = 5,470, r = 0.64, and k = 12. Therefore, for the given function, the value of f(x) decreases by 100(1 – 0.64)%, or 36%, for every increase of x by 12. Since f(x) represents the value, in dollars, of the equipment after x months of use, it follows that the value of the equipment decreases every 12 months by 36% of its value the preceding 12 months. Since there are 12 months in a year, the value of the equipment decreases each year by 36% of its value the preceding year. Thus, the value of
p is 36.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation
We are given the function:
f(x) = 5,470(0.64)x/12,
which represents the value of a piece of equipment (in dollars) after x months of use. The question asks us to determine the percentage p by which the value decreases each year.
Step 1: Understand the Problem
The function uses an exponential decay model of the form:
f(x) = P ⋅ (r)t,
where:
~ P is the initial value (here, P = 5,470),
~ r is the decay factor (here, r = 0.64),
~ t is the time in years.
However, the given function has the time x in months, and the exponent x/12 converts x from months to years.
The value r = 0.64 is the fraction of the value retained after one year, which means 1 − r represents the fraction of the value lost each year. Our goal is to find p = 1 − r expressed as a percentage.
Step 2: Interpret the Decay Factor r = 0.64
The decay factor r = 0.64 indicates that after one year, the equipment retains 64% of its value compared to its value at the beginning of the year. Therefore, the percentage decrease is:
p = 1 − r
p = 1 − 0.64.
Step 3: Calculate p
Simplify the equation:
p = 1 − 0.64
p = 0.36.
Convert p to a percentage by multiplying by 100:
p = 0.36 ⋅ 100
p = 36.
Thus, the equipment decreases by 36% of its value each year.
Step 4: Verify the Answer
We can verify the percentage by reasoning through the exponential decay formula. If the equipment retains 64% of its value each year, then the percentage decrease must be 100% − 64% = 36%, confirming our result.
Final Answer: C) 36.
21th Question
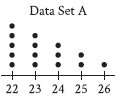
Question: The dot plot represents the 15 values in data set A. Data set B is created by adding 56 to each of the values in data set A. Which of the following correctly compares the medians and the ranges of data sets A and B?
A) The median of data set B is equal to the median of data set A, and the range of data set B is equal to the range of data set A.
B) The median of data set B is equal to the median of data set A, and the range of data set B is greater than the range of data set A.
C) The median of data set B is greater than the median of data set A, and the range of data set B is equal to the range of data set A.
D) The median of data set B is greater than the median of data set A, and the range of data set B is greater than the range of data set A.
Choice C is correct. The median of a data set with an odd number of values, in ascending or descending order, is the middle value of the data set, and the range of a data set is the positive difference between the maximum and minimum values in the data set. Since the dot plot shown gives the values in data set A in ascending order and there are 15 values in the data set, the eighth value in data set A, 23, is the median. The maximum value in data set A is 26 and the minimum value is 22, so the range of data set A is 26 – 22, or 4. It’s given that data set B is created by adding 56 to each of the values in data set A. Increasing each of the 15 values in data set A by 56 will also increase its median value by 56 making the median of data set B 79. Increasing each value of data set A by 56 does not change the range, since the maximum value of data set B is 26 + 56, or 82, and the minimum value is 22 + 56, or 78, making the range of data set B 82 – 78, or 4. Therefore, the median of data set B is greater than the median of data set A, and the range of data set B is equal to the range of data set A.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
To solve this question, let’s analyze the problem in detail, verify the calculations, and understand the changes to both the median and the range of the data when data set B is created.
Step 1: Understanding Data Set A (Original Data)
From the dot plot, we can count the frequencies of the data values in data set A.
| Data Value | Frequency |
|---|---|
| 22 | 5 |
| 23 | 4 |
| 24 | 3 |
| 25 | 2 |
| 26 | 1 |
Total Number of Values:
The total number of values is 5 + 4 + 3 + 2 + 1 =15.
Median of Data Set A:
The median is the middle value when the data is arranged in ascending order. Since there are 15 values, the median is the 8th value in the ordered list.
Ordering the data:
22, 22, 22, 22, 22, 23, 23, 23, 23, 24, 24, 24, 25, 25, 26
The 8th value is 23, so the median of data set A is:
Median of data set A = 23
Finding the Range of Data Set A:
The range is the difference between the largest and smallest values in the data set:
Range of data set A = 26 − 22 = 4
Step 2: Data Set B Analysis
Data Set B is created by adding 56 to each value in Data Set A. Therefore, the values of Data Set B are:
| Data Value | Frequency |
|---|---|
| 78 (22 + 56) | 5 |
| 79 (23 + 56) | 4 |
| 80 (24 + 56) | 3 |
| 81 (25 + 56) | 2 |
| 82 (26 + 56) | 1 |
Finding the Median of Data Set B:
Adding 56 to each value in Data Set A shifts the median by 56 as well. The median of Data Set A was 23, so the median of Data Set B is:
Median of Data Set B = 23 + 56 = 79
Finding the Range of Data Set B:
The range remains the same, as adding a constant to each value does not change the difference between the largest and smallest values:
Range of Data Set B = 26 − 22 = 4
Step 3: Comparing the Medians and Ranges
~ Median Comparison: The median of Data Set B (79) is greater than the median of Data Set A (23) because all values in Data Set B are shifted upward by 56.
~ Range Comparison: The range of Data Set B (4) is equal to the range of Data Set A (4) because adding the same constant to all values does not change the difference between the largest and smallest values.
Step 4: Final Answer
The correct option is: Option C).
22th Question
Question: The equation x2 + (y − 1)2 = 49 represents circle A. Circle B is obtained by shifting circle A down 2 units in the xy-plane. Which of the following equations represents circle B?
A) (x − 2)2 + (y − 1)2 = 49
B) x2 + (y − 3)2 = 49
C) (x + 2)2 + (y − 1)2 = 49
D) x2 + (y + 1)2 = 49
Choice D is correct. The graph in the xy-plane of an equation of the form (x – h)2 + (y – k)2 = r2 is a circle with center (h, k) and a radius of length r. It’s given that circle A is represented by x2 + (y – 1)2 = 49, which can be rewritten as x2 + (y – 1)2 = 72. Therefore, circle A has a center (0, 1) and a radius of length 7. Shifting circle A down two units is a rigid vertical translation of circle A that does not change its size or shape. Since circle B is obtained by shifting circle A down two units, it follows that circle B has the same radius as circle A, and for each point (x, y) on circle A, the point (x, y – 2) lies on circle B. Moreover, if (h, k) is the center of circle A, then (h, k – 2) is the center of circle B. Therefore, circle B has a radius of 7 and the center of circle B is (0, 1 – 2), or (0, -1). Thus, circle B can be represented by the equation x2 + (y + 1)2 = 72, or x2 + (y + 1)2 = 49.
Choice A is incorrect. This is the equation of a circle obtained by shifting circle A right 2 units.
Choice B is incorrect. This is the equation of a circle obtained by shifting circle A up 2 units.
Choice C is incorrect. This is the equation of a circle obtained by shifting circle A left 2 units.
Step-by-Step Explanation
We are tasked with identifying the equation of a circle, Circle B, obtained by shifting Circle A down by 2 units in the xy-plane.
Step 1: Analyze the Original Equation of Circle A
The equation of Circle A is:
x2 + (y − 1)2 = 49.
This is the standard equation of a circle:
(x − h)2 + (y − k)2 = r2,
where:
~ (h, k) is the center of the circle,
~ r is the radius of the circle.
From the given equation:
~ The center of Circle A is (h, k) = (0, 1),
~ The radius is “square root of 49” = 7.
Step 2: Determine the Effect of Shifting the Circle Down
To shift a circle down by 2 units in the xy-plane, only the y-coordinate of the center changes. Specifically:
~ The center of Circle A was at (0, 1),
~ Shifting it down by 2 units gives a new center of (0, 1 − 2) = (0, −1).
The radius remains the same (r = 7).
Step 3: Write the Equation of Circle B
The general equation for a circle with center (h, k) and radius r is
(x − h)2 + (y − k)2 = r2.
For Circle B:
~ The center is (0, −1),
~ The radius is still 7 (r2 = 49).
Substitute these values into the general equation:
(x − 0)2 + [y − (−1)]2 = 49,
which simplifies to:
x2 + (y + 1)2 = 49.
Step 4: Verify the Answer
Among the answer choices, the equation:
x2 + (y + 1)2 = 49
matches the derived equation for Circle B.
Final Answer: D) x2 + (y + 1)2 = 49.
Did you try all the features and get comfortable using them? You should work on using the Desmos calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must attempt as many questions as you can before the final test. This is the 6th Practice Test of SAT Math Module 2nd.
Either you can take the 7th Practice Test of SAT Math or the 7th Practice Test of SAT Reading and Writing Module 2nd.
- SAT Test 7th (Math Module 2nd)
- SAT Test 6th (Math Module 1st)
- SAT Test 6th (Reading and Writing Module 2nd)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


