SAT Math Module 2nd (How to Get 1500+ Hack, Free Test 2025

Question:
$y = x + 1$
$y = x^2 + x$
If $(x, y)$ is a solution to the system of equations above, which of the following could be the value of $x$?
A) -1
B) 0
C) 2
D) 3

🧠 Core Concept (Why substitution is used)
A solution must satisfy both equations at the same time.
So we set them equal.

🧮 Step-by-Step Solution$$x + 1 = x^2 + x$$
Subtract $x$ from both sides:
$1 = x^2\\ x^2 = 1$

Square root on both side or just drop square to right-hand side:
$x = \sqrt{ 1}$

1 square root is 1 – after square root, the value can either be positive or negative
Hence the sign – look below.
$$x = \pm1$$
So:$$x = -1 \quad \text{or} \quad x = 1$$
In option, we have only given -1, so Option A is correct.

Choice B is incorrect. If $x + 1 = 1$, then $x + 1 = 1$, but $x^2 + x = 0^2 + 0 = 0 ≠︀ 1$.

Choice C is incorrect. If $x = 2$, then $x + 1 = 3$, but $x^2 + x = 2^2 + 2 = 6 ≠︀ 3$.

Choice D is incorrect. If $x = 3$, then $x + 1 = 4$, but $x^2 + x = 3^2 + 3 = 12 ≠︀ 4$.

🧮 DESMOS CHECK
1. Enter:
y = x + 1
y = x^2 + x
2. Desmos Graph shows: Intersections at x = −1 and x = 1

Question:
$8j = k + 15m$
The given equation relates the distinct positive numbers $j$, $k$, and $m$. Which equation correctly expresses $j$ in terms of $k$ and $m$?

A) $j = \frac{k}{8} + 15m$

B) $j = k + \frac{15m}{8}$

C) $j = 8(k + 15m)$

D) $j = \frac{k + 15m}{8}$

1️⃣ What the Question Is Asking
~ “Express $j$ in terms of $k$ and $m$” means:
~ Isolate j completely
~ The final equation must look like:
$$j = \text{(something involving only } k \text{ and } m)$$
2️⃣ Formula / Rule Used
Solving a Linear Equation for a Variable
To isolate a variable:
~ Undo addition / subtraction first
~ Undo multiplication / division last
~ Whatever you do to one side, you must do to the other

3️⃣ Step-by-Step Solution
Start with:$$8j = k + 15m$$
Since $j$ is multiplied by 8, divide both sides by 8:
$$\frac{8j}{8} = \frac{k + 15m}{8}$$
Simplify:$$j = \frac{k + 15m}{8}$$
✅ Correct Answer: Option D

❌ $j = \frac{k}{8} + 15m$
~ Only $k$ was divided by 8
~ Division must apply to the entire right-hand expression

❌ $j = k + \frac{15m}{8}$
~ Same mistake: divided only one term
~ This breaks algebraic balance

❌ $j = 8(k + 15m)$
~ Multiplied instead of divided
~ Does the exact opposite of isolating $j$

5️⃣ Desmos ACTUAL Trick
1. Type: 8j = k + 15m
~ Desmos will ask you to input values of j, k, and, m using a Slider.
~ So you have two choice: Either give all value 1 or
~ Replace j to y, k to a, and m to x. This way Desmos will only ask for you to input value of a using a slider.
2. Type Options one-by-one from 2nd line.
~ Replace j, k, and m if you did it on Step 1.
3. Observe:
Notice that Question equation and Option D follows same line, they are on each other. That is your correct answer.

Question: A ball is dropped from an initial height of 22 feet and bounces off the ground repeatedly. The function $h$ estimates that the maximum height reached after each time the ball hits the ground is 85% of the maximum height reached after the previous time the ball hit the ground. Which equation defines $h$, where $h(n)$ is the estimated maximum height of the ball after it has hit the ground $n$ times and $n$ is a whole number greater than 1 and less than 10?
A) $h(n) = 22(0.22)^n$
B) $h(n) = 22(0.85)^n$
C) $h(n) = 85(0.22)^n$
D) $h(n) = 85(0.85)^n$

Understand the Question
~ A ball is dropped from an initial height of 22 feet.
~ Each time it hits the ground, the next maximum height is 85% of the previous height.
~ Which equation defines $h(n)$, where:
$h(n)$ = maximum height after the ball hits the ground $n$ times
$1 < n < 10$

1️⃣ What the Question Is Asking
This describes:
~ A repeated percent decrease
~ Each bounce keeps 85% of the previous height
~ This is an exponential decay model

2️⃣ Formula / Rule Used
Exponential Decay Model$$h(n) = a(r)^n$$
Where:
$a$ = initial value (starting height)
$r$ = decay factor (percent kept, written as a decimal)
$n$ = number of bounces

3️⃣ Step-by-Step Reasoning
Step 1: Identify the initial value
~ Initial height = 22 feet
~ So $a = 22$

Step 2: Convert percent to decimal
~ 85% = 0.85
~ This is the decay factor

Step 3: Write the equation$$h(n) = 22(0.85)^n$$
✅ Correct Answer: Option B

❌ $22(0.22)^n$
~ Used 22% instead of 85%
~ Confused initial height with decay rate

❌ $85(0.22)^n$
~ Used 85 as a starting height (wrong units)
~ Still wrong decay factor

❌ $85(0.85)^n$
~ Correct decay rate, but wrong starting value
~ Initial height is 22, not 85

Question: Line 𝑘 is defined by 𝑦 = $\frac{17}{7}x$ + 4. Line 𝑗 is parallel to line 𝑘 in the 𝑥𝑦-plane. What is the slope of line 𝑗?
A) $\frac{7}{17}$

B) $\frac{17}{7}$
C) 4
D) 17

🧠 Core Concept (Must be known before solving)
~ Parallel lines never intersect
~ Parallel lines have exactly the same slope
~ Only the y-intercept may change
This is a definition, not a trick.

🧮 Step-by-Step Solution
The equation of line $k$ is already written in slope–intercept form:
$$y = mx + b$$
This form is important because:
$m$ = slope
$b$ = y-intercept
From:
$$y = \frac{17}{7}x + 4$$
we directly read:
$$m_k = \frac{17}{7}$$
Because line $j$ is parallel to line $k$, it must have:
$$m_j = m_k$$
So:$$m_j = \frac{17}{7}$$
✅ Correct Answer: B) $\frac{17}{7}$

Option A: $\frac{7}{17}$ ❌
Trap: Student flips the fraction, confusing parallel lines with perpendicular lines.
👉 Flipping happens only for perpendicular lines, not parallel ones.

Option C: 4 ❌
Trap: Student mistakes the y-intercept for the slope.

Option D: 17 ❌
Trap: Student ignores the denominator and assumes slope is just the numerator.

🧮 DESMOS CHECK
1. Enter:
y = (17/7)x + 4
y = (17/7)x – 10
2. The lines never intersect → same slope
✔ Confirmed

Question: $$x + 3 = -2y + 5$$$$x – 3 = 2y + 7$$The solution to the given system of equations is ($x, y$). What is the value of $2x$?
A) −2
B) 6
C) 12
D) 24

🧠 Core Concept
We must:
~ solve the system
~ then compute twice the x-value

🧮 Step-by-Step Solution
Method 1
Step 1: Rewrite both equations to isolate x
First equation: $x + 3 = -2y + 5$
$x = -2y + 5 – 3$
(Sign changed when move from one-side to another or just Subtract both side by 3)
$$x = -2y + 2$$
Second equation: $x – 3 = 2y + 7$
$x = 2y + 7 + 3$
(Sign changed when move from one-side to another or just do Addition on both side by 3)
$$x = 2y + 10$$
Step 2: Set expressions equal (why this works)
Both equal $x$, so: Equation 1 = Equation 2
$$-2y + 2 = 2y + 10$$
Sign changes when move from one-side to another
~ $2y$ on the right-hand side move to left-hand side, so the positive $2y$ becomes, negative $-2y$
~ Left-hand side positive 2 moves to right-hand side and becomes negative -2

$-2y – 2y = 10 – 2$
$-4y = 8$

Step 3: Solve for y
$$-4y = 8$$
$$y = -2$$
Step 4: Find x
Substitute into: Choose any equation whether 1 or 2.

$x = 2y + 10 \\ x = 2(-2) + 10 \\ x = -4 + 10 \\ x = 6$

Step 5: Compute $2x$
If $x$ is 6 then what will be its double: $6 \times 2$
$$2x = 12$$
✅ Correct Answer: C) 12

Method 2:
Equation 1: $x + 3 = -2y + 5$
Equation 2: $x – 3 = 2y + 7$

Adding Equation 2 to Equation 1, in order to find 2x

$(x + 3) + (x -3) = (-2y + 5) + (2y + 7) \\ x + x + 3 -3 = -2y + 2y + 5 + 7 \\ 2x = 12$

✅ Correct Answer: C) 12

Option A (−2) ❌
Trap: Student gives $y$ instead of $2x$.

Option B (6) ❌
Trap: Student stops after finding $x$.

Option B (6) ❌
Trap: Student stops after finding $x$.

🧮 Desmos Confirmation
1. Open Desmos
2. Enter:
x + 3 = -2y + 5
x – 3 = 2y + 7
3. Check the graph:
~ Shows three intersection (0, -5), (6, -2), and (10, 0)
~ we know (x, y)
~ There are three x given in graph: (x = 0), (x = 6), and (x = 10)
~ but we need double of x
~ means x multiplied by 2
~ there are no options like 0 or 20, so we pick
Intersection at $(6, -2)$ → $2x = 12$

Question:
$\frac{2(x+1)}{x+5} = 1 – \frac{1}{x+5}$
What is the solution to the equation above?
A) 0
B) 2
C) 3
D) 5

Understand the Question$$\frac{2(x+1)}{x+5} = 1 – \frac{1}{x+5}$$
What the Question Is Asking
Solve the equation and find the value of $x$ that makes both sides equal, keeping in mind domain restrictions.

Important Rules / Concepts
~ Fractions with the same denominator can be combined.
~ Never allow the denominator to be zero.
$$x + 5 \neq 0 \Rightarrow x \neq -5$$
~ Clearing fractions by multiplying both sides by the LCD avoids mistakes.

Step-by-Step Solution
Step 1: Identify the common denominator$$x + 5$$
Step 2: Multiply both sides by x+5
You can either multiply both sides with x+5 or notice that there are two sides and what we normally do at this point, is either cross multiply or the value in divide / denominator goes to other side as multiplication.
$$(x+5)\cdot \frac{2(x+1)}{x+5} = (x+5)\left(1 – \frac{1}{x+5}\right)$$
Step 3: Simplify
Left side: We cut (x + 5) to (x + 5).$$2(x+1)$$
Right side:
$(x + 5) (1 – \frac{1}{x +5}) \\ \\ 1 \times (x + 5) – \frac{1}{x +5} \times (x +5)$
1 will multiply with (x + 5) and after Minus sign, we cut both x + 5 to (x + 5).
We are left with:
$(x + 5) – 1 \\ \\x + 5 – 1 \\ \\ x + 4$

So: Left-hand side and right-hand side are:
$$2x + 2 = x + 4$$
Step 4: Solve
$2x + 2 = x + 4 \\ \\ 2x – x = 4 – 2 \\ \\ x = 2$

Check the Solution
Substitute $x = 2$:
$\frac{2(x+1)}{x+5} = 1 – \frac{1}{x+5} \\ \\ \frac{2(2+1)}{2+5} = 1 – \frac{1}{2+5} \\ \\ \frac{2(3)}{7} = 1 – \frac{1}{7} \\ \\ \frac{6}{7} = \frac{1}{1} – \frac{1}{7} \\ \\ \frac{6}{7} = \frac{7 – 1}{7} \\ \\ \frac{6}{7} = \frac{6}{7}$
✔ Valid solution.
Correct Answer: Option B$$\boxed{2}$$

Why Other Options Are Wrong
0 → does not balance both sides
3 → fails when substituted
5 → incorrect algebra result

Common Student Mistakes
❌ Forgetting to multiply every term by the denominator
❌ Cancelling incorrectly
❌ Not checking the solution

Desmos Trick (Actual)
Type: 2(x+1)/(x+5) = 1 – 1/(x+5)
Desmos shows the intersection at x = 2.

Question: Ages of 20 Students Enrolled in a College Class

The table above shows the distribution of ages of the 20 students enrolled in a college class. Which of the following gives the correct order of the mean, median, and mode of the ages?
A) mode < median < mean
B) mode < mean < median
C) median < mode < mean
D) mean < mode < median

Understanding the Question
You are given the ages of 20 students and how often each age appears.
You are asked to determine the correct order of:
Mean
Median
Mode
This is a data interpretation + statistics question.

Important Definitions / Rules
Mean = average = (sum of all values) ÷ (number of values)
Median = middle value when data is ordered
Mode = most frequent value
⚠️ In right-skewed data (a few large values pulling the data right):
$$\text{mode} < \text{median} < \text{mean}$$

Step-by-Step Solution
Step 1: Identify the Mode
From the frequency table:

Highest frequency = 6
Mode = 18

Step 2: Find the Median
There are 20 students, so the median is the average of the 10th and 11th values.
Cumulative count:
Ages 18 → positions 1–6
Ages 19 → positions 7–11
So:
10th value = 19
11th value = 19
👉 Median = 19

Step 3: Reason About the Mean
There is a large outlier (age 30) that pulls the average upward.
So:$$\text{Mean} > \text{Median}$$
Final Order$$\boxed{\text{mode} < \text{median} < \text{mean}}$$
✅ Correct Answer: mode < median < mean

Why Other Options Are Wrong
mean < mode < median ❌
Mean is the largest due to skew.

mode < mean < median ❌
Mean is larger than median here, not smaller.

median < mode < mean ❌
Mode (18) is smaller than median (19).

Question: A bus traveled on the highway and on local roads to complete a trip of 160 miles. The trip took 4 hours. The bus traveled at an average speed of 55 miles per hour (mph) on the highway and an average speed of 25 mph on local roads. If $x$ is the time, in hours, the bus traveled on the highway and $y$ is the time, in hours, it traveled on local roads, which system of equations represents this situation?
A)
$55x + 25y = 4$
$x + y = 160$
B)
$55x + 25y = 160$
$x + y = 4$
C)
$25x + 55y = 4$
$x + y = 160$
D)
$25x + 55y = 160$
$x + y = 4$

Understand the Question
A bus traveled a total of 160 miles in 4 hours.
~ Speed on highway = 55 mph
~ Speed on local roads = 25 mph
~ $x$ = time (hours) on highway
~ $y$ = time (hours) on local roads
Which system of equations represents this situation?

🧠 Core Concept (Why two equations are needed)
This is a rate × time = distance problem.
We always build:
1. Distance equation
2. Time equation

🧮 Step-by-Step Explanation
Step 1: Build the distance equation (this is the key)
Distance = (speed)(time)
~ Highway distance = $55x$
~ Local road distance = $25y$
Total distance:
$$55x + 25y = 160$$
This equation must equal miles, not hours.

Step 2: Build the time equation
The total time spent traveling is 4 hours.
$$x + y = 4$$
~ Only Option B matches both correct equations.
✅ Correct Answer: B

Option A ❌
~ Uses distance equation = 4 (wrong units)
~ Uses time equation = 160 (wrong units)
Trap: Student swaps miles and hours.

Option C ❌
Trap: Student swaps highway and local speeds.

Option D ❌
Trap: Student uses correct structure but wrong speed placement.

Question: For a snowstorm in a certain town, the minimum rate of snowfall recorded was 0.6 inches per hour, and the maximum rate of snowfall recorded was 1.8 inches per hour. Which inequality is true for all values of $s$, where $s$ represents a rate of snowfall, in inches per hour, recorded for this snowstorm?
A) $s \ge 2.4$
B) $0.6 \le s \le 1.8$
C) $s \ge 1.8$
D) $0 \le s \le 0.6$

🧠 Core Concept
When a value is between a minimum and a maximum, we use a compound inequality:
$$\text{minimum} \le \text{value} \le \text{maximum}$$

🧮 Step-by-Step Solution
The snowfall rate:
~ Cannot be less than 0.6
~ Cannot be greater than 1.8
So all valid values of $s$ satisfy:
$$0.6 \le s \le 1.8$$
✅ Correct Answer: B) $0.6 \le s \le 1.8$

Option A: s ≥ 2.4 ❌
Trap: Student incorrectly adds the min and max.

Option C: s ≥ 1.8 ❌
Trap: Student uses only the maximum and ignores the minimum.

Option D: 0 ≤ s ≤ 0.60 ❌
Trap: Student assumes snowfall starts at zero and stops at minimum.

🧮 DESMOS CHECK
Type: 0.6 ≤ s ≤ 1.8
This shades exactly the valid region.
✔ Confirmed

Question: Circle $B$ has a radius of 6 millimeters (mm). Circle $D$ has an area of $64 \pi\ mm^2$. What is the total area, in $mm^2$, of circles $B$ and $D$?
A) $36 \pi$
B) $64 \pi$
C) $78 \pi$
D) $100 \pi$

Understanding the Question
You are given two circles:
Circle B → radius is known
Circle D → area is already given
You are asked to find the total area of both circles.

Important Formula / Rule
The area of a circle is:$$A = \pi r^2$$

Step-by-Step Solution
Step 1: Area of Circle B
Radius of Circle B:$$r = 6 \text{ mm}$$
Apply the area formula:$$A_B = \pi (6)^2 = 36\pi$$
Step 2: Area of Circle D
Given directly:$$A_D = 64\pi$$
Step 3: Total Area$$A_{\text{total}} = 36\pi + 64\pi = 100\pi$$
Correct Answer: Option D$$\boxed{100\pi}$$

Why Other Options Are Incorrect
36π ❌ Only area of circle B
64π ❌ Only area of circle D
78π ❌ Incorrect addition

Common Student Mistakes
Ignoring the given area of one circle
Forgetting to square the radius
Adding radii instead of areas

Use DESMOS as a calculator only.

Question:
$k(j) = \frac{3}{5}j + \frac{7}{6}$
$r(j) = 6j – 5$
The functions $k$ and $r$ are defined by the equations shown. Which expression is equivalent to $k(j) \cdot r(j)$?

A) $\frac{18j^2}{5} – \frac{35}{6}$

B) $\frac{18j^2}{5} + \frac{27j}{11} – \frac{35}{6}$

C) $\frac{18j^2}{5} – 4j – \frac{35}{6}$

D) $\frac{18j^2}{5} + 4j – \frac{35}{6}$

Important Rules
~ Use distributive property (FOIL).
~ Multiply every term carefully.
~ Combine like terms.

Step-by-Step Solution

$k(j) \cdot r(j) = (\frac{3}{5}j + \frac{7}{6}) (6j – 5)$

Distribute:
Step 1: Multiply each pair$$\frac{3}{5}j \cdot 6j = \frac{18j^2}{5}$$$$\frac{3}{5}j \cdot (-5) = -3j$$
$$\frac{7}{6} \cdot 6j = 7j$$$$\frac{7}{6} \cdot (-5) = -\frac{35}{6}$$
Step 2: Combine like terms$$-3j + 7j = 4j$$
Final expression:$$\frac{18j^2}{5} + 4j – \frac{35}{6}$$
Correct Answer: Option D$$\boxed{\frac{18j^2}{5} + 4j – \frac{35}{6}}$$

Why Other Options Are Wrong
A → missing the middle $j$-term
B → incorrect coefficient of $j$
C → sign error on the linear term

Common Student Mistakes
❌ Forgetting one distributive multiplication
❌ Combining unlike terms
❌ Sign error

Desmos Trick
1. Type the question equation: replace j to x.
~ First line: k(x) = 3/5 x + 7/6
~ Second line: r(x) = 6x – 5
2. Type options from 3rd line one-by-one: 18x^2 /5 + 4x – 35/6
3. Observe the graph: Option D and question line on graph.
~ The intersect points of both k(x) and r(x) matches exactly to Option D.
~ Focus on Intersect points.
OR
If it is difficult for you then do one simple thing.
Consider any value of j like j = 2.
Now, all you need to do is to type:
Question equations in multiply form like asked and options but filling value j.
The Option D output will be the same as questions.

Question: A model predicts that a certain animal weighed 241 pounds when it was born and that the animal gained 3 pounds per day in its first year of life. This model is defined by an equation in the form $f(x) = a + bx$, where $f(x)$ is the predicted weight, in pounds, of the animal $x$ days after it was born, and $a$ and $b$ are constants. What is the value of $a$?

[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

Understand the Question
A model predicts:
~ Animal weighed 241 pounds at birth
~ Gained 3 pounds per day
The model is:
$$f(x) = a + bx$$
where:
$f(x)$ = weight after $x$ days
$a, b$ are constants
What is the value of $a$?

🧠 Core Concept (Critical)
In:
$$f(x) = a + bx$$
$a$ = starting value (when $x = 0$ days)
$b$ = rate of change

🧮 Step-by-Step Solution
Since, we were not given “any time “how many days” in question, so we focus on:
“At birth” means:
$$x = 0$$Substitute into the model:
$$f(0) = a + b(0) = a$$
The problem states:
$$f(0) = 241$$
So:
$$a = 241$$
✅ Correct Answer: 241

❌ 244
Mistake: Student adds one day of growth immediately:
$$241 + 3 = 244$$
They forget that $a$ represents before any growth occurs.

❌ 3
Mistake: Student confuses rate of change $b$ with starting value $a$.

❌ 0
Mistake: Student assumes all models start at zero.

🧮 DESMOS CONFIRMATION
1. Enter: f(x) = 241 + 3x
2. Check: x = 0 → f(0) = 241
✔ Confirms $a = 241$

Question: $\sqrt[3]{x^3 y^6}$
Which of the following expressions is equivalent to the expression above?
A) $y^2$
B) $xy^2$
C) $y^3$
D) $xy^3$

Important Rules$$\sqrt[n]{a^m} = a^{m/n}$$$$\sqrt[3]{x^3} = x \quad \sqrt[3]{y^6} = y^2$$

Step-by-Step Solution
Split the cube root:$$\sqrt[3]{x^3 y^6} = \sqrt[3]{x^3}\cdot \sqrt[3]{y^6}$$
Simplify each part:

$\sqrt[3]{x^3}\ \to\ x^\frac{3}{3}\ \to\ x \\ \\ \sqrt[3]{y^6}\ \to\ y^\frac{6}{3}\ \to\ y^2$$$x \cdot y^2 = xy^2$$
Correct Answer: Option B$$\boxed{xy^2}$$

Why Other Options Are Wrong
y² → ignores the $x$ term
y³ → wrong exponent
xy³ → incorrect root simplification

Common Student Mistakes
❌ Dividing exponents incorrectly
❌ Forgetting variables under the radical
❌ Mixing square-root and cube-root rules

Desmos Trick
Use Desmos as a calculator. It would be better you solve it like above, but if you want to use Desmos then assign values to x and y.
x = 2.
y = 2.
You can choose any values, now all you need to do is to find output of question and options to figure it which matches exactly.

Question: Two customers purchased the same kind of bread and eggs at a store. The first customer paid 12.45 dollars for 1 loaf of bread and 2 dozen eggs. The second customer paid 19.42 dollars for 4 loaves of bread and 1 dozen eggs. What is the cost, in dollars, of 1 dozen eggs?
A) 4.34
B) 4.15
C) 3.88
D) 3.77

Understand the Question
Two customers purchased the same kind of bread and eggs.
~ Customer 1:
1 loaf of bread + 2 dozen eggs = $12.45
~ Customer 2:
4 loaves of bread + 1 dozen eggs = $19.42
What is the cost of 1 dozen eggs?

🧠 Concept Used (Why this is a system)
We are buying two items (bread and eggs), so we must use:
~ two variables
~ two equations
Let:
$e$ = cost of 1 dozen eggs
$b$ = cost of 1 loaf of bread

🧮 Step-by-Step Solution
Step 1: Write equations from the word problem
Customer 1:
$$b + 2e = 12.45$$
Customer 2:
$$4b + e = 19.42$$
Step 2: Solve the system (elimination method)
To eliminate $e$, multiply the second equation by 2:
$$8b + 2e = 38.84$$
Now subtract the first equation:
$$(8b + 2e) – (b + 2e) = 38.84 – 12.45$$
$$7b = 26.39$$
$$b = 3.77$$
Step 3: Substitute to find eggs cost
Substitute $b = 3.77$ into:
$$b + 2e = 12.45$$
$$3.77 + 2e = 12.45$$
$$2e = 8.68$$
$$e = 4.34$$
✅ Correct Answer: A) 4.34

Option B: 4.15 ❌
Trap: Student divides incorrectly when solving $2e = 8.68$.

Option C: 3.88 ❌
Trap: Student mistakenly reports bread price instead of egg price.

Option D: 3.77 ❌
Trap: Student stops after finding $b$ and forgets question asks for eggs.

🧮 DESMOS METHOD
1. Enter:
b + 2e = 12.45
4b + e = 19.42
2. Use intersection
3. Read value of $e$
✔ Confirms $e = 4.34$

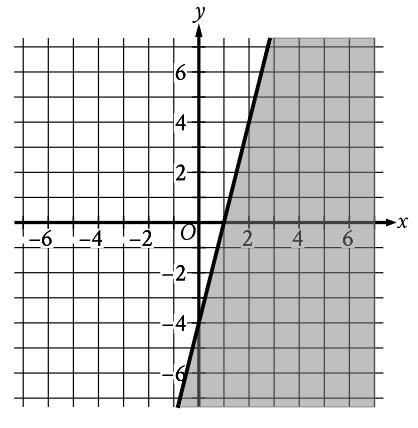
Question: The shaded region shown represents the solutions to an inequality. Which ordered pair ($x$, $y$) is a solution to this inequality?
A) (6, −2)
B) (1, 4)
C) (−2, 5)
D) (−5, −6)

🧠 Concept Used
A solution must lie inside the shaded area
~ Right side of the line = valid
~ Left side = invalid
~ Inequality solutions are regions, not single values, so focus where both x and y touch

🧮 Step-by-Step Visual Reasoning
From the graph:
~ The shaded region is to the right of the line
~ The line slopes upward
We should not focus on individual x or y. We should focus on the point they both touch.

Check each option:
(6, −2) ✅
x = 6 → far to the right
$y = -2$ → slightly below the x-axis
When plotted:
~ This point is clearly inside the shaded area
✔ This satisfies the inequality

Option B: (1,4) ❌
$x = 1$ → close to the y-axis
~ This point lies to the left of the boundary line
Even though $y$ is positive:
~ The point is outside the shaded region
✘ Not a solution
Trap: Students assume “positive y” means shaded — wrong.

Option C: (−2,5) ❌
~ Negative x
~ Upper-left quadrant
This point is entirely on the unshaded side
✘ Not a solution
Trap: Students think “higher y = valid” — incorrect for inequalities.

Option D: (−5,−6) ❌
~ Far left
~ Far down
Clearly outside the shaded region
✘ Not a solution

🧮 (Confirmation, Not Replacement) — Desmos Check
In Desmos:
1. Plot the boundary line
2. Plot point $(6, -2)$
3. The point appears inside the shaded half-plane
✔ Confirms visual reasoning
✘ Desmos is not the main reasoning, only confirmation\

Question: The measure of angle $Z$ is $60^\circ$. What is the measure, in radians, of angle $Z$?
A) $\frac{1}{6} \pi$

B) $\frac{1}{3} \pi$

C) $\frac{2}{3} \pi$

D) $1 \pi$

Understanding the Question
You are asked to convert degrees to radians.
Important Conversion Rule$$\text{Radians} = \text{Degrees} \times \frac{\pi}{180^\circ}$$

Step-by-Step Solution
Step 1: Substitute the Angle$$60^\circ \times \frac{\pi}{180}$$
Step 2: Simplify$$\frac{60\pi}{180} = \frac{\pi}{3}$$
Correct Answer: Option B
$\frac{1 \pi}{3} = \frac{\pi}{3}$
Both are the same.

Why Other Options Are Incorrect
π/6 ❌ Equals 30°
2π/3 ❌ Equals 120°
π ❌ Equals 180°

Common Student Mistakes
Cancelling π incorrectly
Forgetting to divide by 180
Confusing radians with degrees

Use DESMOS as a calculator.

Question:
$$3x = 36y – 45$$One of the two equations in a system of linear equations is given. The system has no solution.
Which equation could be the second equation?

A) $x = 4y$
B) $\frac{1}{3}x = 4y$
C) $x = 12y – 15$
D) $\frac{1}{3}x = 12y – 15$

🔑 What “NO SOLUTION” Means (Applied, Not Theory)
A system has no solution when:
~ The two lines are parallel
~ Same slope
~ Different intercepts, so they never intersect
This condition will guide every step below.

🧮 Rewrite the given equation in comparable form
Given (The most important step to solve it):
$$3x = 36y – 45$$
Divide every term by 3 or move 3 to right-hand side into divide position:
$$x = 12y – 15$$
Now this equation is in a clean form where we can clearly see:
~ Slope = 12
~ Intercept = −15
This rewritten form is the reference equation.

✅ OPTION B — CORRECT ANSWER

$\tfrac{1}{3}x = 4y$

Step 1: Rewrite Option B
Multiply both sides by 3: or just move 3 to right-hand side like this (4y multiply by 3)
$$x = 12y$$
Step 2: Compare with the given equation
Given:
$$x = 12y – 15$$
Option B:
$$x = 12y$$
Now compare carefully:

✔ Same slope
✔ Different intercepts

Final Conclusion for Option B
~ Same slope → parallel lines
~ Different intercepts → never meet
✅ No solution
✅ Option B is correct

❌ OPTION A — THE REAL TRAP
$x = 4y$

Why Option A FEELS Correct to Many Students
Students often think:
~ “The system has no solution”
~ “So the equations must be different”
~ “This equation looks simpler and different”
~ “Maybe any different equation works”
That thinking is dangerous.

Rewrite Option A Properly
$$x = 4y$$
Compare with: Simplify form of 3x = 36y – 45
$$x = 12y – 15$$
Now compare slopes:
~ Given equation slope = 12
~ Option A slope = 4
Since the slopes are different, the lines are not parallel.

What That Means
~ Different slopes → lines must intersect
~ Intersecting lines → one solution
But the question says: The system has NO solution
So Option A cannot be correct.
❌ Option A is a trap caused by ignoring slopes

❌ OPTION C

$x = 12y – 15$

This is identical to the given equation.
That means:
~ Same line
~ Infinite intersection points
This produces infinitely many solutions, not “no solution.”
❌ Incorrect

❌ OPTION D

$\tfrac{1}{3}x = 12y – 15$

Multiply both sides by 3:
$$x = 36y – 45$$
This is exactly the original equation given in the question.
Again:
~ Same line
~ Infinite solutions
❌ Incorrect

🧮 DESMOS CALCULATOR — SAT-REALISTIC CONFIRMATION
Step-by-Step in Desmos
1. Open Desmos
2. In Expression Line 1, type: x = 12y – 15
3. In Expression Line 2, type: x = 12y (Simplify all options then type one by one to check)
4. Observe the graph:
~ Two straight lines
~ Same direction
~ Never intersect
5. Zoom in and out using the zoom controls
6. No intersection point appears
✔ Confirms no solution

Question: A data set of 27 different numbers has a mean of 33 and a median of 33. A new data set is created by adding 7 to each number in the original data set that is greater than the median and subtracting 7 from each number in the original data set that is less than the median. Which of the following measures does NOT have the same value in both the original and new data sets?
A) Median
B) Mean
C) Sum of the numbers
D) Standard deviation

Understanding the Question
There are 27 different numbers
Mean = 33
Median = 33
A transformation is applied:
~ Numbers greater than the median → add 7
~ Numbers less than the median → subtract 7
~ The median itself (33) is unchanged
We must determine which statistical measure changes after this transformation.

Key Rules / Concepts
Median → middle value (position-based)
Mean → depends on the total sum
Sum → total of all values
Standard deviation → measures spread (distance from mean)

Step-by-Step Reasoning
New and Old Changes or Not
Median
~ There are 27 numbers → the median is the 14th value
~ That value is 33
~ The transformation does not change the median itself
✅ Median stays the same

Mean & Sum: 13 + 1 + 13 = 27
~ There are 13 numbers below 33 → each gets –7
~ There are 13 numbers above 33 → each gets +7
~ Net change in sum:$$13(+7) + 13(-7) = 0$$
$91 – 91 = 0$
✅ Sum stays the same
✅ Mean stays the same

Standard Deviation
~ Values move farther away from the mean
~ Spread increases
❌ Standard deviation changes

Correct Answer: Option D$$\boxed{\text{Standard deviation}}$$

Why Other Options Are Incorrect
Median ❌ unchanged
Mean ❌ unchanged
Sum ❌ unchanged

Common Student Trap
Thinking “numbers changed, so mean must change” — ignoring symmetry.

Question: Which of the following expressions is equivalent to $(sin 24^\circ)(cos 66^\circ) + (cos 24^\circ)(sin 66^\circ)$?
A) $2(cos 66^\circ)(sin 24^\circ)$
B) $2(cos 66^\circ) + 2(cos 24^\circ)$
C) $(cos 66^\circ)^2 + (cos 24^\circ)^2$
D) $(cos 66^\circ)^2 + (sin 24^\circ)^2$

Question Explanation
We are given the expression:$$(\sin 24^\circ)(\cos 66^\circ) + (\cos 24^\circ)(\sin 66^\circ)$$
We are asked to find which option is equivalent to this expression.
This is a trigonometric identity recognition question, not a numerical approximation question.

Important Formula / Rule Used
🔑 Sine Addition Identity$$\sin(A + B) = \sin A \cos B + \cos A \sin B$$
This identity is exactly in the same structure as the given expression.

Option C$$(\cos 66^\circ)^2 + (\cos 24^\circ)^2$$
✅ CORRECT
Why this works:
Use the complementary-angle identity: $90 – 24 = 66$
$$\sin \theta = \cos(90^\circ – \theta)$$
$\sin 24^\circ = \cos 66^\circ$
$\sin 66^\circ = \cos 24^\circ$
Substitute into the original expression: $(sin 24^\circ)(cos 66^\circ) + (cos 24^\circ)(sin 66^\circ)$
$$(\cos 66^\circ)(\cos 66^\circ) + (\cos 24^\circ)(\cos 24^\circ)$$
Which becomes:$$(\cos 66^\circ)^2 + (\cos 24^\circ)^2$$
✔ Exact match
Final Answer
✅ Correct Option: C$$\boxed{(\cos 66^\circ)^2 + (\cos 24^\circ)^2}$$

Option A$$2(\cos 66^\circ)(\sin 24^\circ)$$❌ Incorrect
Why:
This doubles only one product term and ignores the second term entirely.
The identity does not allow combining terms this way.
Common student mistake:
Thinking “two similar terms” exist when they do not.

Option B$$2(\cos 66^\circ) + 2(\cos 24^\circ)$$
❌ Incorrect
Why:
The original expression involves products, not sums.
You cannot convert multiplication into addition in trig identities.
Student trap:
Confusing distributive property with trigonometric identities.

Option D$$(\cos 66^\circ)^2 + (\sin 24^\circ)^2$$
❌ Incorrect (VERY subtle error)
Why it looks tempting:
Because $\sin 24^\circ = \cos 66^\circ$
But here’s the mistake:
$$(\cos 66^\circ)^2 + (\sin 24^\circ)^2 = (\cos 66^\circ)^2 + (\cos 66^\circ)^2 = 2(\cos 66^\circ)^2$$
That is not equal to:$$(\cos 66^\circ)^2 + (\cos 24^\circ)^2$$
Since:$$\cos 66^\circ \neq \cos 24^\circ$$
Student mistake pattern:
Replacing only one angle correctly, but failing to check whether both squared terms represent different values.

Question:
2(8x) + 4(7y) = 12
-2(8x) + 4(7y) = 12
The solution to the given system of equations is (x, y). What is the value of 8x + 7y?

[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

3 is correct. You must be thinking, this explanation is too big, but fear not, we have explained every possible ways to solve this equation. Take it educational that clears your concepts.

🧮 Step-by-Step Correct Solution
2(8x) + 4(7y) = 12 ……….. Equation 1
-2(8x) + 4(7y) = 12 ………. Equation 2
There are two Methods:
Method 1: (With Simplification)
Step 1: Simplify both equations carefully
First equation:
2(8x) + 4(7y) = 12
16x + 28y = 12 (Equation 1)

Second equation:
−2(8x) + 4(7y) = 12
−16x + 28y = 12 (Equation 2)

Step 2: Eliminate a variable
Subtract Equation 2 from Equation 1:
Equation 1 – Equation 2
(16x + 28y) − (−16x + 28y) = 12 − 12
16x + 28y +16x – 28y = 0
16x + 16x + 28y – 28y = 0
32x = 0
x = 0 / 32
x = 0

Method 2: (Without Simplification)
Just use the whole equations from start and Subtract Equation 2 from Equation 1:
2(8x) + 4(7y) = 12 ……….. Equation 1
-2(8x) + 4(7y) = 12 ………. Equation 2
[2(8x) + 4(7y) = 12] – [-2(8x) + 4(7y) = 12]
(16x + 28y) – (-16x + 28y) = 12 – 12
16x + 28y + 16x – 28y = 0
16x + 16x + 28y – 28y = 0
32x = 0
x = 0 / 32
x = 0.

But What if – instead of Subtracting, we do Addition:
2(8x) + 4(7y) = 12 ……….. Equation 1
-2(8x) + 4(7y) = 12 ………. Equation 2
[2(8x) + 4(7y) = 12] + [-2(8x) + 4(7y) = 12]
(16x + 28y) + (-16x + 28y) = 12 + 12
16x + 28y – 16x + 28y = 24
16x – 16x + 28y + 28y = 24
56y = 24
y = 24 / 56
y = 3 / 7
(The same Addition is used in Method 1 also.)

Now, suppose, you only found one whether x or y. All you need to do is to put value in any one equation.
Let’s pick Equation 1 to fill x-value to find out y:
x = 0
2(8x) + 4(7y) = 12 ……….. Equation 1
2(8 . 0) + 4(7y) = 12
2(0) + 28y = 12
28y = 12
y = 12 / 28
y = 3 / 7

Let’s pick Equation 2 to fill y-value to find out x:
y = 3 / 7
-2(8x) + 4(7y) = 12 ………. Equation 2

We know (x = 0) and (y = 3 / 7).

Final Step: Compute 8x + 7y

✅ Final Answer: 3​

🧮 DESMOS METHOD (FAST & SAFE)
1. Open Desmos
2. Expression Line 1: 16x + 28y = 12
3. Expression Line 2: -16x + 28y = 12
4. Click the intersection point → Desmos shows (x, y): (0, 3/7)
5. New Expression Line: 8x + 7y
6. Desmos evaluates it as: 3

Question: A grove has 6 rows of birch trees and 5 rows of maple trees. Each row of birch trees has 8 trees 20 feet or taller and 6 trees shorter than 20 feet. Each row of maple trees has 9 trees 20 feet or taller and 7 trees shorter than 20 feet. A tree from one of these rows will be selected at random. What is the probability of selecting a maple tree, given that the tree is 20 feet or taller?
A) $\frac{9}{164}$

B) $\frac{3}{10}$

C) $\frac{15}{31}$

D) $\frac{9}{17}$

Understanding the Question
We are asked: Probability that a randomly selected tall tree (≥ 20 ft) is a maple tree
This is a conditional probability.

Key Formula of Probability$$P(\text{Maple} \mid \text{Tall}) = \frac{\text{Tall maple trees}}{\text{All tall trees}}$$

Step-by-Step Solution
Birch Trees: b
6 rows × 8 tall trees = 48 tall birch trees

Maple Trees: m
5 rows × 9 tall trees = 45 tall maple trees

Total Tall Trees: b + m$$48 + 45 = 93$$
Conditional Probability of Maple Trees:$$P = \frac{45}{93}$$
Simplify:$$\frac{45}{93} = \frac{15}{31}$$
Correct Answer: Option C$$\boxed{\frac{15}{31}}$$

Why Other Options Are Incorrect
9/164 ❌ uses total trees instead of tall trees
3/10 ❌ random guess
9/17 ❌ incorrect simplification

Common Student Mistake
Using all trees instead of only tall trees in the denominator.

DESMOS Tricks
1. Type: 45/(48+45)
2. Type Options one-by-one in different lines:
15/31
3. Output: 0.4838…
Option C will be the same as the question equation.

Question: A window repair specialist charges $220 for the first two hours of repair plus an hourly fee for each additional hour. The total cost for 5 hours of repair is $400. Which function f gives the total cost, in dollars, for x hours of repair, where x ≥ 2?
A) $f(x) = 60x + 100$
B) $f(x) = 60x + 220$
C) $f(x) = 80x$
D) $f(x) = 80x + 220$

Option A is correct.
🧮 STEP-BY-STEP SOLUTION
The question gives three critical pieces of information:
1. $220 covers the first 2 hours — this is a fixed starting cost
2. $x \ge 2$ : Any time after 2 hours is charged per hour – this is a variable cost
3. 5 total hours cost $400
The phrase “first two hours” and the condition $x \ge 2$ are the key signals that this is not a simple hourly rate from zero.

Step 1: Identify the fixed cost
The specialist charges:
$$\$220 \text{ for the first 2 hours}$$
This amount is charged no matter what, as long as $x \ge 2$.
So $220 must appear as a constant term in the function.
Immediately, this eliminates any option without +220.
❌ Eliminate:
~ Option A
~ Option C

Step 2: Use the given total cost to find the hourly rate
We are told:
~ Total hours = 5
~ Total cost = $400
Out of these 5 hours:
~ First 2 hours cost $220
~ Remaining hours (x) = $5 – 2 = 3$ hours
So the cost of the additional 3 hours is:
$$400 – 220 = 180$$
Now find the hourly fee: (Divided by 3 hours)
$$\frac{180}{3} = 60$$
So the additional hourly charge is:
$$\$60 \text{ per hour}$$

Step 3: Build the function correctly
For $x \ge 2$:
~ Fixed cost = 220
~ Hourly cost applies to all x hours, but the constant already accounts for the first 2 hours
So the total cost function must be:
$$f(x) = 60x + 220$$
✅ Correct Answer: B) $f(x) = 60x + 220$

Option A: f(x) = 60x + 100 ❌
Why students choose this:
~ They subtract incorrectly:
$$220 – 120 = 100$$
~ They try to “adjust” the constant without logic
Why it fails:
At $x = 2$:
$$f(2) = 60(2) + 100 = 220 \quad (\text{looks correct})$$
But at $x = 5$:
$$f(5) = 300 + 100 = 400$$
This works only accidentally and does not represent the pricing structure correctly.
SAT checks modeling, not coincidence.
❌ Rejected

Option C: f(x) = 80x ❌
Why students choose this:
~ They divide total cost by total hours:
$$\frac{400}{5} = 80$$
This assumes:
~ No fixed cost
~ Same rate from hour 1
That directly contradicts the problem statement.
❌ Rejected

Option D: f(x) = 80x + 220 ❌
Why students choose this:
They combine both mistakes:
~ Wrong hourly rate
~ Double-counting the fixed fee
Check at $x = 5$:
$$80(5) + 220 = 620$$
❌ Way too large

🧮 DESMOS CALCULATOR — SAT-CONFIRMATION METHOD
Step-by-Step
1. Open Desmos
2. In Expression Line 1, type: f(x) = 60x + 220
3. In Expression Line 2, type: x = 5
4. Use the Table icon:
~ Enter x = 5
~ Observe output aligns with the pricing structure
5. Compare with other options by replacing the equation
Only Option B models:
~ Fixed first cost
~ Correct additional hourly rate
~ Valid for $x \ge 2$
✅ FINAL ANSWER
$$\boxed{f(x) = 60x + 220}$$