SAT Math Module 1st (How to Get 1500+ Hack, Free Test 2024

Question: If $2x + 3 = 9$, what is the value of $6x – 1$?

[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

17 is correct.
Step 1: Solve for $x$
We have given: $2x + 3 = 9$
$2x = 9 – 3$
$2x = 6$
$\\ x = \frac{6}{2}$ (6 divided by 2)
$x = 3.$

Step 2: Substitute into 6x – 1
Now we know x is 3, let’s solve.
6(3) – 1
18 – 1
17.
✅ Final Answer: 17.

🧮 DESMOS METHOD (VERY PRECISE)
Method 1: Table (Fastest)
1. Open Desmos
2. In Expression Line: 2x + 3 = 9
3. Click solution → Desmos shows: x = 3
4. New line: 6x – 1
5. Desmos shows: 17
✅ Confirmed

Question: The function $f$ is defined by $f(x) = 8x$. For what value of $x$ does $f(x) = 72$?
A) 8
B) 9
C) 64
D) 80

✅ Correct Answer: B) 9

🧮 Correct Solution — Step by Step
We are told:
$f(x) = 8x$ and $f(x) = 72$
That means: $8x = 72$
[For what value of $x$ does $f(x) = 72$? Take it as “Makes / Gives.” For what value of $x$ makes $f(x) = 72$.]

Step 1: Isolate x
Divide both sides by 8 or simple solve it like this: $8x = 72$
$$x = \frac{72}{8}$$
Step 2: Compute
$x = 9$
✔ So, the correct value of $x$ is 9.

Choice A is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

🧮 DESMOS CALCULATOR — SAT-REALISTIC METHOD
Method 1: Graph Intersection (Most Visual)
1. Open Desmos
2. In Expression Line 1, type: y = 8x
3. In Expression Line 2, type: y = 72
4. Click the intersection point
Desmos displays: (9, 72)
✔ x-value = 9

Method 2: Table (Fastest on SAT)
1. Click the Table icon next to y = 8x
2. Try values from options:
x = 8 → y = 64
x = 9 → y = 72 ✅
✔ Confirmed
✅ FINAL ANSWER: 9

Question: A printer produces posters at a constant rate of 42 posters per minute. At what rate, in posters per hour, does the printer produce the posters?
A) 2520
B) 102
C) 18
D) 1.42

✅ Understand the QUESTION
Unit Conversion (Rate Problem)
Given:
~ Printer rate = 42 posters per minute
~ Asked: posters per hour

🧠 Step-by-Step Solution
Step 1: Identify the conversion factor$$1 \text{ hour} = 60 \text{ minutes}$$

Step 2: Multiply the rate$$42 \times 60 = 2520$$
2520 ✅ Option A

102 ❌
Addition instead of multiplication.

18 ❌
Subtract instead of multiplication.

1.42 ❌
Division instead of multiplication.

🧮 Desmos Check
1. Type: 42*60
2. Output: 2520

Question:
$5|x| = 45$
What is the positive solution to the given equation?
A) 40
B) 50
C) 9
D) -9

🧠 Step-by-Step Mathematical Solution
We are given an equation involving absolute value:
$$5|x| = 45$$
Step 1: Isolate the absolute value
Divide both sides by 5 because it is multiplying |x|:
$$|x| = 9$$
Step 2: Interpret absolute value
The equation |x| = 9 means:$$x = 9 \quad \text{or} \quad x = -9$$
Step 3: Apply the question condition
The question asks for the positive solution only.
So we select:$$\boxed{9}$$

40 ❌
A student choosing 40 likely:
~ Multiplied 5 × 9 incorrectly
~ Subtract 45 – 5 incorrectly
~ Or misunderstood absolute value as multiplication
No step leads to 40.

50 ❌
This comes from:$$5 \times 10 = 50$$
Guessing instead of solving.

-9 ❌
This is a solution, but:
The question explicitly asks for the positive solution

🧮 Desmos Calculator (Correct Usage)
1. Open Desmos
2. Type: 5|x| = 45
3. Desmos shows two intersection points: x = 9 and x = -9
4. Select the positive x-value
✅ Final answer confirmed: 9

Question: Triangles $EFG$ and $JKL$ are congruent, where $E$ , $F$, and $G$ correspond to $J$, $K$, and $L$, respectively. The measure of angle $E$ is $45^{\circ}$ and the measure of angle $F$ is $20^{\circ}$. What is the measure of angle $J$?
A) $20^{\circ}$
B) $45^{\circ}$
C) $135^{\circ}$
D) $160^{\circ}$

✅ Understand the QUESTION
Congruent Triangles & Corresponding Angles
Given:
~ Triangles EFG and JKL are congruent
~ Correspondence is stated clearly:
$$E \leftrightarrow J,\quad F \leftrightarrow K,\quad G \leftrightarrow L$$
$\angle E = 45^\circ$
$\angle F = 20^\circ$
Asked:
What is the measure of $\angle J$?

🧠 Key Geometry Rule (Very Important)
Congruent triangles have equal corresponding angles and sides.
Since:$$E \leftrightarrow J$$
It directly means:$$\angle J = \angle E$$

✏️ Step-by-Step Solution$$\angle J = 45^\circ$$
No calculation needed beyond recognizing correspondence.
✅ Correct: Option B

20° ❌
That is $\angle F$, not $\angle E$.
SAT trap: mixing up corresponding vertices.

135° ❌
This would be the third angle if added incorrectly.
SAT trap: unnecessary angle sum calculation.

160° ❌
Impossible for a triangle angle here.

📌 Student Reminder
Always match letters first in congruent triangle problems before doing any math.

Question: Which expression is equivalent to $23x^2 + 2x^2 + 9x$?
A) $23x(x² + 2x + 9)$
B) $9x(23x³ + 2x² + 1)$
C) $x(23x² + 2x + 9)$
D) $34(x³ + x² + x)$

🧠 Step-by-Step Mathematical Solution
Step 1: Factor out the greatest common factor (GCF)
$23x^2 + 2x^2 + 9x$
Both terms contain x:
$x(23x² + 2x + 9)$
This is the simplified equivalent expression.
✅ Option C.

VERIFICATION:
Expand again: $x(23x² + 2x + 9)$
$\\ x(23x² + 2x + 9)\\ \\x \times 23x^2 + x \times 2x + x \times 9\\ \\ 23x^3 + 2x^2 + 9x$

A ❌
Expands to:$$23x^3 + 46x^2 + 207x$$
Not equal to the original expression.

B ❌
Introduces x³, which never appeared originally.
SAT trap: unnecessary higher powers.

D ❌
Factor 34 does not match any coefficient in the original expression.

🧮 Desmos Verification
1. Type: 23x^2 + 2x^2 + 9x
2. Type all options one-by-one
3. You will notice that the Option C line in graph will be on the Question expression.
~ Both same will be same. That is your correct option in graph.

Question: A store sells two different-sized containers of a certain Greek yogurt. The store’s sales of this Greek yogurt totaled 1,277.94 dollars last month. The equation $5.48x + 7.30y = 1,277.94$ represents this situation, where $x$ is the number of smaller containers sold and $y$ is the number of larger containers sold. According to the equation, which of the following represents the price, in dollars, of each smaller container?
A) 5.48
B) 7.30y
C) 7.30
D) 5.48x

Choice A is correct.
🧮 Step-by-Step Solution
This equation represents total revenue, built using the structure:
$$(\text{price per item}) \times (\text{number of items})$$
Look carefully at the term involving x, because:
~ x represents the number of smaller containers
~ The coefficient multiplying $x$ represents the price per smaller container
From the equation:
$$5.48x + 7.30y$$
~ 5.48x: revenue from smaller containers
~ 7.30y: revenue from larger containers
So the price per smaller container is the coefficient of $x$.
✅ Correct Answer: A) 5.48

Option B: 7.30y ❌
Trap: Student sees the larger price but forgets the question asks for smaller containers.

Option C: 7.30 ❌
Trap: Student identifies a price but for the wrong container size.

Option D: 5.48x ❌
Trap: Student includes the variable.
This represents total revenue from smaller containers, not the price per container.

🧮 DESMOS CONFIRMATION
1. Open Desmos
2. Type: 5.48x + 7.30y = 1277.94
3. Observe coefficients: Coefficient of $x$ → price per smaller container
✔ Confirmed

Question: What is the area, in square inches, of a rectangle with a length of 7 inches and a width of 6 inches?
A) 13
B) 20
C) 42
D) 84

✅ Understand the QUESTION
Area of a Rectangle
Given:
~ Length = 7 inches
~ Width = 6 inches
Asked:
Area in square inches

🧠 Geometry Formula$$\text{Area of rectangle} = \text{length} \times \text{width}$$
✏️ Calculation$$7 \times 6 = 42$$
✅ Correct Answer: 42

13 ❌
Adds sides instead of multiplying.
SAT trap: perimeter thinking.

20 ❌
Random incorrect operation.

84 ❌
Doubles the area incorrectly.

📌 Student Reminder
Area uses multiplication, not addition.

DESMOS CALCULATION:
1. Type: 7*6
2. Output = 42.

Question: At the time of posting a video, a social media channel had 53 subscribers. Each day for five days after the video was posted, the number of subscribers doubled from the number the previous day. Which equation gives the total number of subscribers, $n$, to the channel $d$ days after the video was posted?
A) $n = 53^d$
B) $n = 53(2)^d$
C) $n = 53(\frac{1}{2})^2$
D) $n = 53^2 + d$

✅ Understand the QUESTION
Subscribers Growth Problem
~ At posting: 53 subscribers
~ Each day for 5 days, subscribers double
~ Which equation gives the total number of subscribers n after d days?

🧠 Step-by-Step Mathematical Solution
Step 1: Identify the growth type
The subscribers double each day.
Doubling means:$$\text{Exponential growth with base } 2$$
Step 2: Identify the starting value
At day 0:$$n = 53$$
Step 3: Write the exponential model
General form:$$n = a(b)^d$$
Where:
$a = 53$ (initial value)
$b = 2$ (doubling factor)
$d =$days
So:$$\boxed{n = 53(2)^d}$$
✅ Option B.

A ❌
Raises 53 to a power — incorrect.
Growth factor must be 2, not 53.

C ❌
Represents decay, not growth.

D ❌
Linear expression — doubling is not linear.

Question: Each face of a fair 14-sided die is labeled with a number from 1 through 14, with a different number appearing on each face. If the die is rolled one time, what is the probability of rolling a 2?
A) $\frac{1}{14}$

B) $\frac{2}{14}$

C) $\frac{12}{14}$

D) $\frac{13}{14}$

✅ Understand the QUESTION
Basic Probability (Uniform Outcomes)
Given:
~ Fair 14-sided die
~ Faces labeled 1 through 14
~ Rolled once
Asked: Probability of rolling a 2

🧠 Step-by-Step Solution
Step 1: Count total outcomes$$14 \text{ possible outcomes}$$
Step 2: Count favorable outcomes
Rolling a 2:$$1 \text{ favorable outcome}$$
Step 3: Probability formula
Rolled Once: Rolled only 1 time
$$P = \frac{\text{favorable}}{\text{total}} = \frac{1}{14}$$
1/14 ✅ Option A

2/14 ❌
Would mean rolling two numbers at once.

12/14 ❌
Probability of not rolling 1 or 2.

13/14 ❌
Probability of not rolling 2.

Question: The function $f$ is defined by $f(x) = 10x^2 – 32x – 152$. What is the value of $f(0)$?
A) -152
B) -32
C) 0
D) 10

🧠 Step-by-Step Mathematical Solution
Step 1: Understand what $f(0)$ means
It means substitute x = 0 into the function.

Step 2: Substitute carefully$$f(0) = 10(0)^2 – 32(0) – 152$$$$= 0 – 0 – 152$$$$= -152$$$$\boxed{-152}$$
✅ Correct: Option A.

-32 ❌
Trap: students mistakenly use the linear coefficient.

0 ❌
Trap: assuming everything becomes zero when x = 0.

10 ❌
Trap: confusing coefficient of $x^2$ with function value.

🧮 Desmos Check
1. Type: f(x)=10x^2-32x-152
2. Type: f(0)
or
Just use slider to adjust x = 0
3. Desmos outputs: -152

Question: Triangle $R$ has an area of 80 square centimeters $(cm^2)$. Square $S$ has side lengths of $4\ cm$ What is the total area of triangle $R$ and square $S$, in $cm^2$?
A) 42
B) 44
C) 84
D) 96

✅ Understand the QUESTION
Total Area (Triangle + Square)
Given:
~ Area of Triangle R = 80 cm²
~ Square S has side length = 4 cm
Asked:
Total area of triangle R and square S

🧠 Step 1: Area of the Square
Square Area Formula:$$\text{Area} = \text{side}^2$$$$4^2 = 16$$
🧠 Step 2: Add the Areas$$80 + 16 = 96$$
✅ Correct Answer: 96

42 ❌
Incorrect square area calculation.

44 ❌
Adds incorrect square area.

84 ❌
Uses side length instead of area.

📌 Student Reminder
When adding areas, find each shape’s area first, then add.

DESMOS TRICKS:
1. Type 4^2
2. Output: 16
3. Type in next line: 80+16
4. Output: 96

Question:
$(x+2)(x−5)(x+9)=0$
What is a positive solution to the given equation?
A) 3
B) 4
C) 5
D) 18

🧠 Step-by-Step Mathematical Solution
This equation is already factored, which tells us exactly what to do.
Step 1: Use the Zero Product Property
If a product equals zero, at least one factor must be zero.
So we set each factor equal to 0:
$$x + 2 = 0 \Rightarrow x = -2$$$$x – 5 = 0 \Rightarrow x = 5$$$$x + 9 = 0 \Rightarrow x = -9$$
Step 2: Identify the positive solution
The solutions are:$$-2,\; 5,\; -9$$
Only 5 is positive and given in Option C.$$\boxed{5}$$

3 ❌
Comes from guessing or dividing numbers randomly.
Not a root of any factor.

4 ❌
A common guess because it is “near 5.”
SAT trap: estimation instead of solving.

18 ❌
Product confusion trap.
SAT students sometimes multiply constants:$$2 \times 5 \times 9 = 90$$
which is irrelevant.

🧮 Desmos (Correct Method)
1. Type: (x+2)(x-5)(x+9)=0
2. Desmos shows x-intercepts at: -9, -2, 5
3. Choose the positive intercept
✅ Answer confirmed: 5

Question: In the $xy$-plane, line $t$ passes through the points (0, 9) and (1, 17). Which equation defines line $t$?
A) $y = \frac{1}{8}x + 9$
B) $y = x + \frac{1}{8}$
C) $y = x + 8$
D) $y = 8x + 9$

🧠 Core Concept Used
To define a line, we need:
~ Slope $m$
~ y-intercept $b$
We use slope–intercept form:
$$y = mx + b$$

Choice D is correct.
🧮 Step-by-Step Solution
Step 1: Find the slope (why slope first)
A line is uniquely determined by how steep it is and where it crosses the y-axis.
Slope tells us how much y changes when x increases by 1.
Slope formula:
$$m = \frac{y_2 – y_1}{x_2 – x_1}$$
Using the given points:
$$(0, 9),\ (1, 17)$$
~ ($x_1$, $y_1$) = (0, 9)
~ ($x_2$, $y_2$) = (1, 17)
$$m = \frac{17 – 9}{1 – 0} = \frac{8}{1} = 8$$
So the slope is 8.

Step 2: Identify the y-intercept (why this is immediate)
The point $(0, 9)$ lies on the line.
When $x = 0$:
$$y = b$$
So:
$$b = 9$$
Step 3: Write the equation
$$y = 8x + 9$$
✅ Correct Answer: D) $y = 8x + 9$

Option A: $y = \frac{1}{8}x + 9$ ❌
Trap: Student flips the slope.
~ Correct slope = 8
~ This option uses the reciprocal, a very common SAT mistake.

Option B: $y = x + \frac{1}{8}$​ ❌
Trap: Student mixes slope and intercept incorrectly.
~ Slope should be 8, not 1
~ Intercept should be 9, not $\frac{1}{8}$

Option C: y = x + 8 ❌
Trap: Student subtracts instead of calculating slope.
Confuses vertical change with intercept value

🧮 Desmos Confirmation
1. Type: y = 8x + 9
2. Check:
x = 0 → y = 9
x = 1 → y = 17
✔ Verified

Question: If the graph of 27𝑥 + 33𝑦 = 297 is shifted down 5 units, what is the y-intercept of the resulting graph?
A) (0, 4)
B) (0, 6)
C) (0, 14)
D) (0, 28)

🧠 Core Concept Used
~ The y-intercept is where $x = 0$
~ A vertical shift down 5 units subtracts 5 from every y-value

🧮 Step-by-Step Solution
Step 1: Find the original y-intercept
Set $x = 0$:
$$27(0) + 33y = 297$$
$$33y = 297$$
$$y = 9$$
Original y-intercept:
$$(0, 9)$$
Step 2: Apply the vertical shift (why subtraction)
“Shifted down 5 units” means:
$$y = 9 – 5 = 4$$
Step 3: State the new y-intercept
$$(0, 4)$$
✅ Correct Answer: (0, 4)

Option B: (0, 6) ❌
Trap: Student subtracts 3 instead of 5.

Option C: (0, 14) ❌
Trap: Student adds instead of subtracting.

Option D: (0, 28) ❌
Trap: Student confuses equation constant with intercept.

🧮 Desmos Confirmation
Graph:
27x + 33y = 297
27x + 33(y+5) = 297
✔ New intercept at $y = 4$

Question: Which of the following is equivalent to the expression $b^4 – b^2 – 6$?
A) $(b^2 + 1)(b^2 – 6)$
B) $(b^2 + 2)(b^2 – 3)$
C) $(b^2 + 3)(b^2 – 2)$
D) $(b^2 + 6)(b^2 – 1)$

The Options are Quadratic but the Expression is not
The expression is:$$b^4 – b^2 – 6$$
Key observation (VERY IMPORTANT):
• Powers are 4, 2, and constant
• This is NOT a regular quadratic
• But it is quadratic in terms of $b^2$
👉 This is called a quadratic-in-form expression.

🧠 STEP 1: USE SUBSTITUTION (CORE CONCEPT)
Let:$$u = b^2$$
Why this step?
Because:
• $b^4 = (b^2)^2 = u^2$
• $b^2 = u$
Now rewrite the expression correctly:
$$b^4 – b^2 – 6 \quad \Rightarrow \quad u^2 – u – 6$$
⚠️ This step is non-negotiable.

🧠 STEP 2: FACTOR THE QUADRATIC $u^2 – u – 6$
We now factor:$$u^2 – u – 6$$
How factoring works
We focus on here: $– u – 6$
We need two numbers that:
Multiply to −6: $u_1 \times u_2 = -6$
Add to −1 (coefficient of $u$): $u_1 + u_2 = -1$

What is coefficient?: 3x, here 3 is coefficient but when only x is given then we consider it like this 1x, so 1 is its coefficient.
Coefficient of $-u$ is -1.

Now all we need to do is to find values to put in $u_1$ and $u_2$.
Possible factor pairs of −1 and -6:
• $+2, -3$ → sum = −1 ✅ and $+2 \times -3 = -6$ ✅
• $+1, -6$ → sum = −5 ❌ and $+1 \times -6 = -6$ ❌
• $+3, -2$ → sum = +1 ❌ and $+3 \times-2 = -6$ ❌

✔️ The only valid pair that stands to both condition: +2 and −3
So: $u^2 – u – 6\ =\ 1u^2 – 1u – 6\ =\ ax^2 + bx + c$

Remember above we changed $b^2$ into $u$, so let’s substitute back:
$b^2 = u$

$(u+2)(u−3)$ ⇒ $(b^2 + 2)(b^2 − 3)$

✅ Correct Answer: Option B

❌ $(b^2 + 1)(b^2 – 6)$
Expands to:$$b^4 – 5b^2 – 6$$
Middle term does not match.

❌ $(b^2 + 3)(b^2 – 2)$
Gives:$$b^4 + b^2 – 6$$
Wrong sign on the middle term.

❌ $(b^2 + 6)(b^2 – 1)$
Gives:$$b^4 + 5b^2 – 6$$
Wrong coefficient.

🧮 Real Desmos Verification (Correct Use)
1. Type the question expression first: b^4 – b^2 – 6
2. Type all options one-by-one: ( b^2 + 2 )( b^2 – 3 )
3. Desmos shows both graphs overlap exactly
✅ Confirms equivalence.

Question: The International Space Station orbits Earth at an average speed of 4.76 miles per second. What is the space station’s average speed in miles per hour?
A) 285.6
B) 571.2
C) 856.8
D) 17,136.0

Understand the Question
Unit Conversion (Speed)
Given:
~ Speed = 4.76 miles per second
~ Asked: miles per hour

🧠 Step-by-Step Solution
Step 1: Identify the conversion factor$$1 \text{ hour} = 3600 \text{ seconds}$$

Step 2: Multiply$$4.76 \times 3600 = 17,\!136$$
~ After point / dot, 0 doesn’t matter like in Option D.
17,136.0 = 17,136
✅ Correct Answer: Option D

285.6 ❌
Uses 60 instead of 3600.
SAT trap: converting seconds like minutes.

571.2 ❌
Partial conversion error.

856.8 ❌
Incorrect multiplication.

🧮 Desmos Verification
1. Type: 4.76*3600
2. Output: 17136

Question:
$(2x + 5)^2 – (x – 2) + 2(x + 3)$
Which of the following is equivalent to the expression above?
A) $4x^2 + 21x + 33$
B) $4x^2 + 21x + 29$
C) $4x^2 + x + 29$
D) $4x^2 + x + 33$

🧠 Step-by-Step Mathematical Solution
Step 1: Expand each part separately (prevents errors)
$\\ (2x + 5)^2 – (x – 2) + 2(x + 3)$

The first part: $(2x + 5)^2\ =\ (a + b)^2\ =\ a^2 + 2ab + b^2$
$\\ a = 2x\\ \\b = 5\\ \\a^2 + 2ab + b^2\ =\ (2x)^2 + 2(2x)(5) + (5)^2\ =\ 4x^2 + 20x + 25$

The rest parts: $– (x – 2) + 2(x + 3)$
$\\ -(x – 2) = -x + 2$
$\\ + 2(x + 3) = 2x + 6$

Step 2: Combine all terms$$4x^2 + 20x + 25 – x + 2 + 2x + 6$$
Group like terms:
• $4x^2$
• $20x – x + 2x = 21x$
• $25 + 2 + 6 = 33$

Step 3: Final simplified expression$$\boxed{4x^2 + 21x + 33}$$
✅ Correct: Option A

B ❌
Misses 4 units — common arithmetic slip.

C ❌
Incorrect combination of x-terms.

D ❌
Drops 20x, a classic expansion mistake.

🧮 Desmos Verification
1. Type: (2x+5)^2-(x-2)+2(x+3)
2. Type all options one-by-one: 4x^2+21x+33
~ Look on the graph lines.
3. The Perfect overlap → confirmed the correct option in graph.

Question: A right circular cylinder has a volume of 45$\pi$. If the height of the cylinder is 5, what is the radius of the cylinder?
A) 3
B) 4.5
C) 9
D) 40

✅ Understand the QUESTION
Volume of a Right Circular Cylinder
Given:
~ Volume of cylinder = $45\pi$
~ Height $h = 5$
Asked:
What is the radius of the cylinder?

🧠 Key Geometry Formula$$V = \pi r^2 h$$

✏️ Step-by-Step Solution
Substitute the known values:$$45\pi = \pi r^2(5)$$
Cancel $\pi$ from both sides:$$45 = 5r^2$$
Divide both sides by 5:$$9 = r^2$$
Take square root:$$r = 3$$
✅ Correct Answer: Option A

4.5 ❌
Forgets to square the radius.
SAT trap: treating $r^2$ as $r$.

9 ❌
This is $r^2$, not $r$.

40 ❌
Completely unrelated to the formula.

📌 Concept Reminder
In cylinder problems, radius is always squared in the volume formula.

DESMOS Tricks
1. We know that pi will be divided from both side,
~ and we know h is 5
so: we are left with $45 = 5r^2$
2. Divide 45 to 5:
~ Type: 45/5
~ Output: 9
3. Now all we have: $9 = r^2$
4. Square root of 9:
~ Type: sqrt9
~ Output: 3
We have solved it. For this question, you use DESMOS, just as a calculator.

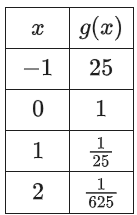
Question: For the exponential function $g$, the table shows four values of $x$ and their corresponding values of $g(x)$. Which equation defines $g$?
A) $g(x) = -25^x$
B) $g(x) = -(\frac{1}{25})^x$
C) $g(x) = 25^x$
D) $g(x) = (\frac{1}{25})^x$

Few Basics You Must Know:
1. Divide a fraction means: $\frac{1}{25} \div 25$
$\\ \frac{1}{25} \times \frac{1}{25} = \frac{1}{625}$, This is how divide works to fraction value.

2. We are learning Math here too, so below I explained how to do but questions like these, you must notice the hidden lines:
~ The table values, look closely to $g(x)$: They are all positive that means, there won’t be any negative value, so Option A and B are out. We are left with Option C and D.

3. How a Negative exponent works: $g(x) = (\frac{1}{25})^x$
$x = -1$
Then,
$g(-1) = (\frac{1}{25})^{-1}$
So -1 as an exponent will flip the fraction if you try to turn it into positive 1 like this:
$g(-1) = (\frac{25}{1})^{1}\\ \\ g(-1) = (25)^{1}\\ \\ g(-1) = 25$

Let’s solve the problem now.

🧠 Step-by-Step Mathematical Reasoning
Step 1: Use the most important exponential rule
For any exponential function:$$g(0) = 1$$
Check the table:$$g(0) = 1$$
✔ Valid exponential model

Step 2: Observe the pattern of change
Look at how values change as x increases:$-1 → 0 → 1 → 2$
$$25 \rightarrow 1 \rightarrow \frac{1}{25} \rightarrow \frac{1}{625}$$
Each step:
~ Divides by 25

This means:
~ The base is $\frac{1}{25}$
~ The function represents exponential decay

Step 3: Write the function
$$g(x) = \left(\frac{1}{25}\right)^x$$
✅ Correct Answer$$\boxed{g(x) = \left(\frac{1}{25}\right)^x}$$
Correct option: D

Option A ❌
$-25^x$
~ Always negative
~ Table values are positive

Option B ❌
$-(\frac{1}{25})^x$
~ Always negative
~ Table values are positive

Option C ❌
$25^x$
At $x = 1$:$$25^1 = 25$$
But table shows:$$\frac{1}{25}$$
Wrong direction (growth vs decay)

🧮 Desmos (ACTUAL & PROPER USE)
1. Type all the values on the table in different lines:
(-1,25)
(0,1)
(1,1/25)
(2,1/625)
2. You will see points on the graph of all 4 values from the table with their respective color.
3. Type all options one-by-one:
g(x) = (1/25)^x
4. Observe:
~ You will see all 4 points are exactly on the curve of Option D.
✅ Verified perfectly

Question: The first term of a sequence is 4. Each term after the first is 9 times the preceding term. If $m$ represents the $t$th term of the sequence, which equation gives $m$ in terms of $t$?
A) $m = 9(4^t)$
B) $m = 9(4^{t-1})$
C) $m = 4(9^t)$
D) $m = 4(9^{t-1})$

Understand the Question
Given
~ First term of the sequence = 4
~ Each term after the first is 9 times the preceding term
~ $m$ represents the $t$th term
Which equation gives $m$ in terms of $t$?

The phrase:
“Each term after the first is 9 times the preceding term”
tells us this is a geometric sequence.
For a geometric sequence, the general formula is: $t$th term = $a \cdot r^{t-1}$
So why there is -1 in exponent
Let’s understand Geometric Sequence.
Each term after the first is 9 times the preceding term.
~ Term 1: 4
~ Term 2: in 2nd term, the 9 start 1st time = $4(9^{2 – 1})\ =\ 4(9^1)$.
~ Term 3: in 3rd term, the 9 start 2nd time = $4(9^{3 – 1})\ =\ 4(9^2)$.
~ Term 4: in 4th term, the 9 start 3rd time = $4(9^{4 – 1})\ =\ 4(9^3)$.
~ Term 5: in 5th term, the 9 start 4th time = $4(9^{5 – 1})\ =\ 4(9^4)$.
~ Term 6: in 6th term, the 9 start 5th time = $4(9^{6 – 1})\ =\ 4(9^5)$.
~ Term 7: in 7th term, the 9 start 6th time = $4(9^{7 – 1})\ =\ 4(9^6)$.
~ Term 8: in 8th term, the 9 start 7th time = $4(9^{8 – 1})\ =\ 4(9^7)$.
~ Term 9: in 9th term, the 9 start 8th time = $4(9^{9 – 1})\ =\ 4(9^8)$.
The 9 times are done.

➡️ The exponent is always one less than the term number
➡️ That is why the exponent is $t−1$, not $t$
This comes directly from the phrase “The first term of a sequence is 4″ in the question.

🧠 Step-by-Step Mathematical Solution
🔹 Step 1: Identify the type of sequence
Each term is multiplied by 9 to get the next term.
That means this is a geometric sequence.

🔹 Step 2: Recall the general formula for a geometric sequence
For a geometric sequence: $t$th term = $a \cdot r^{t-1}$
Where:
$a$ = first term
$r$ = common ratio
$t$ = term number

🔹 Step 3: Substitute known values
From the problem:
~ First term $a = 4$
~ Common ratio $r = 9$$$m = 4 \cdot 9^{t-1}$$
✅ Correct Answer: Option D

A) $9(4^t)$ ❌
Trap:
~ Uses 4 as the ratio
~ Incorrect structure for a geometric sequence

B) $9(4^{t-1})$ ❌
Trap:
~ Swaps the first term and the ratio
~ SAT trap: wrong base in the exponent

C) $4(9^t)$ ❌
Trap:
~ Starts exponent at $t$t, not $t-1$
~ This would make the first term:$$4(9^1) = 36 \neq 4$$

Step-by-Step Solution
Step 1: Calculate the Value of q
The problem states that q is 75% less than 60. To find q:
q = 60 − (75%  of 60)
q = 60 − 0.75 × 60
q = 60 − 45
Thus, q = 15.

Step 2: Calculate the Value of p
The problem states that p is 85% greater than q. This means p is equal to q plus 85% of q. To find p:
p = q + (85% of q)
p = q + 0.85 × q
p = 15 + 0.85 × 15
p = 15 + 12.75 = 27.75
Thus, p = 27.75.

Verification
~ Calculated q = 15 as 75% less than 60.
~ Calculated p = 27.75 as 85% greater than q.
Both steps are consistent with the problem’s conditions.

Final Answer: D) 27.75

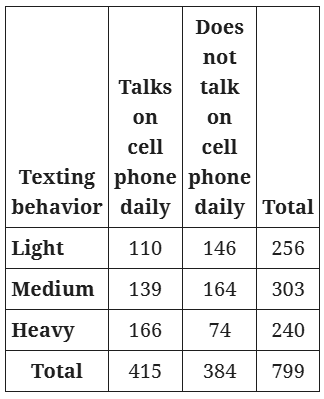
Question: In a study of cell phone use, 799 randomly selected US teens were asked how often they talked on a cell phone and about their texting behavior. The data are summarized in the table above. Based on the data from the study, an estimate of the percent of US teens who are heavy texters is 30% and the associated margin of error is 3%. Which of the following is a correct statement based on the given margin of error?
A) Approximately 3% of the teens in the study who are classified as heavy texters are not really heavy texters.
B) It is not possible that the percent of all US teens who are heavy texters is less than 27%.
C) The percent of all US teens who are heavy texters is 33%.
D) It is doubtful that the percent of all US teens who are heavy texters is 35%.

✅ Understand the QUESTION
Margin of Error & Statistical Interpretation
Given:
~ Sample size = 799 US teens
~ Estimated percent of heavy texters = 30%
~ Margin of error = ±3%
Question:
Which statement is correct based on the margin of error?

🧠 Step 1: Understand what “margin of error” actually means
Margin of error describes a range of plausible values for the true population percentage, not the sample.
So we compute the interval:$$30\% \pm 3\% \Rightarrow [27\%, 33\%]$$
This means:
~ The true percent of all US teens who are heavy texters is likely between 27% and 33%
~ Values outside this range are unlikely, but not mathematically impossible
This interpretation is the core SAT concept.

D ✅ (Correct)
“It is doubtful that the percent of all US teens who are heavy texters is 35%.”
35% is outside the interval $[27\%, 33\%]$.
That makes it:
~ statistically unlikely
~ but not claimed as impossible
✔️ This matches the correct statistical interpretation.

A ❌
“Approximately 3% of the teens in the study who are classified as heavy texters are not really heavy texters.”
Margin of error:
❌ does NOT talk about misclassification
❌ does NOT describe individual errors
❌ does NOT refer to sample accuracy
This option completely misunderstands margin of error.

B ❌
“It is not possible that the percent of all US teens who are heavy texters is less than 27%.”
Margin of error does not say “impossible”.
It says: Values outside the interval are unlikely, not impossible
Absolute language = SAT red flag.

C ❌
“The percent of all US teens who are heavy texters is 33%.”
33% is only the upper bound of the interval, not a confirmed value.
Margin of error never gives an exact population value.