
The SAT Examination Test of 2025 (Math Module 1st with Detailed Solutions and Desmos Tricks
SAT math seems tough without Desmos Calculator but we have solution for this. This test is a practice test of 2025 SAT Math Module First. Here, you would see questions that were possible to be on 2025 examination. The best parts are:
- solutions of all questions,
- step-by-step explanations,
- how to verify the correct answer,
- description of correct and incorrect options,
- tips and tricks,
- and Desmos Calculator Hacks.
Like the other exams, it has the same format and all the necessary features for you to become a SAT master in math. You just take the Module 1st exam to practice your skills. The best part is that you practice within the time limit, and there are explanations of answers, tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each split into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math 2025 Practice Test Module 1st.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 1ST
The first module of Math in SAT contains four segments: “Algebra,’ ‘Advanced Math,’ ‘Problem-Solving and Data Analysis,’ and ‘Geometry and Trigonometry.” The questions in Module 1st are from easy to difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam: Tips Before Taking Tests
- Previous-and-Next: Like in real SAT exam, you can move freely from one question to another, same things you can do here. You select one option and move forward but you realized something, so you came back and change your option. You can do that here and in the real SAT exam too.
- Timer: On the top of the slide, you will see the timer, it starts from 0 and for Module 1st of Math you will get 35 minutes to finish 22 questions. Always try to finish the test before 35 minutes.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can take on mobile phone.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Answer All: Even if you do not know the correct answer of a question, still guess it because there is no Negative marking.
- Last Questions: The harder the question, the more marks it will fetch for you. So most likely, you will find later question difficult and more time-consuming, so utilize your time accordingly.
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Wait for the Desmos Calculator to appear.
SAT MATH PROBLEM SOLUTIONS WITH STEP-BY-STEP EXPLANATION
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips and advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer with step-by-step explanation, red shows the Incorrect one, and blue shows Desmos Tips or Tricks.
1st Question
Question: The function is defined by . What is the value of when ?
A) 110
B) 80
C) 57
D) 50
Choice B is correct. Substitute x = 2 is already given, all we have to do is to put the value of x into the equation.
f(x) = 25(x) + 30
f(x) = 25(2) + 30
f(x) = 50 + 30
f(x) = 80.
Choice A is incorrect. This is the value of (25 +30)(2), not 25(2) + 30.
Choice C is incorrect. This is the value of 25 + 2 + 30, not 25(2) + 30.
Choice D is incorrect. This is the value of 25(2), not 25(2) + 30.
🧮 DESMOS METHOD (VERY PRECISE)
Method 1: Table (Fastest)
1. Open Desmos
2. In Expression Line 1, type: f(x) = 25x + 30
3. Click the Table icon
4. Enter: x = 2
5. Desmos shows: f(x) = 80
✅ Confirmed
Method 2: Graph Reading
1. Keep: y = 25x + 30
2. Click on the point at
3. Desmos displays: (2, 80)
2nd Question
Question: There are 55 students in Spanish club. A sample of the Spanish club students was selected at random and asked whether they intend to enroll in a new study program. Of those surveyed, 20% responded that they intend to enroll in the study program. Based on this survey, which of the following is the best estimate of the total number of Spanish club students who intend to enroll in the study program?
A) 11
B) 20
C) 44
D) 55
✅ Understand the QUESTION
Estimation from a Sample (Statistics)
Given:
~ Total students = 55
~ Survey result = 20% intend to enroll
Asked:
Best estimate of total students intending to enroll.
🧠 Step-by-Step Solution
Step 1: Convert percent to decimal
Step 2: Multiply by total students
✅ Correct Answer: Option A
20 ❌
Mistakes percent for number of students.
44 ❌
Uses 80% instead of 20%.
55 ❌
Assumes everyone enrolls.
🧮 Desmos Check
1. Type: 20/100
2. You will get: 0.2
3. Multiply: 0.2*55
4. Output: 11
Or
You can directly type this: 20/100 * 55
3rd Question
Question:
Which of the following inequalities is equivalent to the inequality above?
A)
B)
C)
D)
🧠 Core Concept (Why “equivalent” matters)
Two inequalities are equivalent if:
~ they describe the same solution region
~ one can be obtained from the other by legal algebraic operations
(adding, subtracting, multiplying/dividing by a positive number)
🧮 Step-by-Step Solution
We start with:
Step 1: Look for a common factor
All coefficients (6, −9, 12) are divisible by 3.
Dividing by 3 simplifies the inequality without changing its direction
(because 3 is positive).
✅ Correct Answer: B)
Option A: ❌
Trap: Student divides incorrectly by 6 instead of 3.
Option C: ❌
Trap: Student swaps coefficients incorrectly.
Option D: ❌
Trap: Student rearranges terms and forgets to flip signs.
🧮 Desmos Confirmation (Correct Way)
Enter both: together option-by-option
6x – 9y > 12
2x – 3y > 4
The shaded regions overlap exactly, confirming equivalence.
4th Question
Question:
For the linear function , is a constant and . What is the value of ?
A) 7
B) 0
C) 1
D) 4
Option B: It is given . So substitute :
f(x) = 4x + b
28 = 4(7) + b
28 = 28 + b
28 – 28 = b
0 = b or b = 0
Choice A is incorrect and may result from conceptual or calculation errors. Assuming b = x.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
🧮 DESMOS METHOD
1. Expression Line: 4(7) + b = 28
2. Solve → b = 0
5th Question
Question:
How many distinct real solutions are there to the given equation?
A) Exactly one
B) Exactly two
C) Infinitely many
D) Zero
🧠 Core Concept (Quadratic roots logic)
A quadratic equation:
has:
~ no real solutions if the discriminant
~ one real solution if the discriminant
~ two real solutions if the discriminant
🧮 Step-by-Step Solution
Method 1:
Step 1: Factor the equation (why factoring first)
All terms share a factor of 3.
Step 2: Factor the quadratic
Rules & Steps: (Ignore 3)
~
~
~
~
Choose a number for
~~ when multiply, it gets 6 =
~~ when do addition, it gets 5 =
Step 3: Solve
These are two different real numbers.
✅ Correct Answer: Exactly two
Method 2:
🔑 The Discriminant Rule (This Is the Formula Used)
The discriminant is:
And the rules are:
~ If → exactly two distinct real solutions
~ If → exactly one real solution
~ If → zero real solutions
This rule is absolute, no exceptions.
We are given:
Identify coefficients carefully (this step matters):
Step 1: Compute the discriminant:
Step 2: Interpret the value
Positive discriminant means:
~ the graph crosses the x-axis twice
~ the equation has two different real x-values
✅ Correct Answer: Exactly two
Exactly one ❌
Trap: Student assumes repeated root without checking factorization.
Infinitely many ❌
Trap: Would only occur if equation reduced to .
Zero ❌
Trap: Student assumes quadratic has no real roots by default.
🧮 Desmos Confirmation
Enter: y = 3x^2 – 15x + 18
Graph crosses x-axis at x = 2 and x = 3.
6th Question
Question: The perimeter of triangle ABC is 17 inches, the length of side AB is 4 inches, and the length of side AC is 7 inches. What is the length, in inches, of side BC?
A) 4
B) 6
C) 7
D) 11
✅ Understand the QUESTION — Triangle Perimeter
Question Explained
You are given:
~ Total perimeter of triangle inches
~ Side inches
~ Side inches
You are asked to find the remaining side BC.
📐 Important Rule / Formula
Triangle Perimeter Formula
This is a definition, not a trick.
🧠 Step-by-Step Solution
Substitute known values:
Combine known sides:
Subtract 11 from both sides:
✅ Correct Answer: Option B
❌ Why Other Options Are Incorrect
~ 4 → assumes two sides are equal (not stated)
~ 7 → repeats an already given side
~ 11 → adds known sides instead of subtracting from perimeter
⚠️ Common Student Mistake: forgetting that perimeter means sum of all three sides, not just two.
🧮 Desmos Trick (Simple Check)
1. Type: 17 – (4 + 7)
2. Desmos outputs 6
7th Question
Question:
The graphs of the given equations in the xy-plane intersect at the point . What is a possible value of ?
A)
B) -9
C) 5
D) 76
Mathematical solution (algebra first)
At an intersection point, both y-values are equal, so:
Add 5 to both sides or just move to right-hand side:
Take square roots:
After root the sign can be either positive or negative.
From the options:
~ The −9 is present
~ The +9 is NOT listed in option
Correct answer: −9
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the value of coordinate y, rather than x, of the intersection point (x, y).
Desmos – real intersection method
1. Open desmos.com/calculator
2. Enter:y = 76y = x^2 - 5
3. Desmos automatically shows intersection points
4. Click the intersection dots
5. Desmos displays:
(−9, 76)
(9, 76)
6. Match with options → −9
✔ This is the standard SAT Desmos intersection trick
8th Question
Question:
The equation shown gives the estimated amount of diesel , in gallons, that remains in the gas tank of a truck after being driven miles, where 0 ≤ ≤ 480. What is the estimated amount of diesel, in gallons, that remains in the gas tank of the truck when = 300?
A) 0
B) 6
C) 14
D) 16
Choice B is correct.
🧮 Step-by-Step Solution
We are asked to evaluate the function at a specific value, so we directly substitute .
Step 1: Substitute
Step 2: Simplify division first
Step 3: Subtract
✅ Correct Answer: B) 6
Option A: 0 ❌
Trap: Student subtracts incorrectly and assumes empty tank.
Option C: 14 ❌
Trap: Student subtracts instead of .
Option D: 16 ❌
Trap: Student forgets to subtract and uses starting amount.
🧮 DESMOS CONFIRMATION
1. Open Desmos
2. Type: d = 16 – x/30
3. Use Table icon
4. Enter: x = 300
5. Output shows: d = 6
✔ Confirmed
9th Question
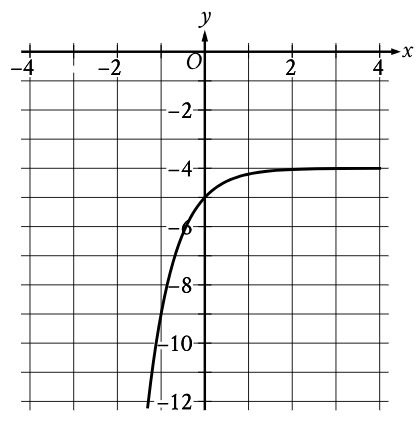
Question: What is the y-intercept of the graph shown?
A. (-1, -9)
B. (0, -5)
C. (0, -4)
D. (0, 0)
Mathematical solution
~ The y-intercept is the point where the graph crosses the y-axis.
~ On the y-axis, x = 0 by definition.
~ (x, y)
~ Looking carefully at the graph, when x = 0, the graph crosses the y-axis at y = −5.
~ Therefore, the y-intercept is (0, −5).
Correct answer: (0, −5)
Choice A is incorrect and may result from conceptual errors.
Choice C is incorrect. This is the y-intercept of a graph in the xy-plane that intersects the y-axis at y = -4, not y = -5.
Choice D is incorrect. This is the y-intercept of a graph in the xy-plane that intersects the y-axis at y = 0, not y = -5.
10th Question
Question: A rectangle has a length of 3 units and a width of 39 units. Which expression gives the area, in square units, of this rectangle?
A)
B)
C)
D)
✅ Understand the QUESTION — Area of a Rectangle
Question Explained
You are given:
~ Length = 3 units
~ Width = 39 units
You are asked for an expression that gives the area.
📐 Important Rule / Formula
Area of a Rectangle
This is a must-know SAT formula.
🧠 Step-by-Step Solution
Substitute values:
Since the question asks for an expression, not a numerical value, we keep it as:
✅ Correct Answer: Option D
❌ Why Other Options Are Incorrect
~ 2(3+39) → perimeter formula, not area
~ 2(3 ⋅ 39) → doubles the area incorrectly
~ 3+39 → adds dimensions (no geometric meaning)
⚠️ SAT Trap: confusing area with perimeter.
11th Question
Question: Which expression is equivalent to ?
A)
B)
C)
D)
🧠 Core Concept (Why “like terms” rule applies)
Only terms with the same variable AND same exponent can be combined.
🧮 Step-by-Step Algebra
Group like terms:
(only appears once)
(only appears once)
So the result is:
✅ Correct Answer: A
Option B ❌
Trap: Student adds exponents instead of coefficients.
Option B ❌
Trap: Student adds exponents instead of coefficients.
Option D ❌
Trap: Student applies subtraction instead of addition.
🧮 ✅ PROPER DESMOS METHOD
1. Enter both expressions separately
A = 9x^3 + 5x + 7
B = 6x^3 + 5x^2 – 5
2. Add them
A + B
Desmos simplifies automatically to: 15x^3 + 5x^2 + 5x + 2
12th Question
Question: Line 𝑝 is defined by 2𝑦 + 18𝑥 = 9. Line 𝑟 is perpendicular to line 𝑝 in the 𝑥𝑦-plane. What is the slope of line 𝑟?
A) -9
B)
C)
D) 9
Choice C is correct.
🧮 Complete Step-by-Step Solution
The question asks for the slope of line r, but line is not given directly.
Instead, we are told it is perpendicular to line .
That means the only possible way forward is:
1. First find the slope of line p
2. Then use the perpendicular-slope rule to find the slope of line
Step 1: Why we isolate y
The equation of line is:
To identify slope, we must write the equation in slope–intercept form:
This form is essential because:
~ The slope is explicitly visible as the coefficient of
~ Perpendicular slope rules apply directly to
That is why we isolate y, not .
Step 2: Isolate
Start with:
Subtract from both sides:
Now divide every term by 2:
Step 3: Identify the slope of line
From:
The slope of line is:
This value controls everything that follows.
Step 4: Apply the perpendicular-line rule
For perpendicular lines:
Substitute :
Solve for :
This is also described as taking the negative reciprocal:
~ Reciprocal of →
~ Change the sign →
✅ Correct Answer: C)
Option A: −9 ❌
Trap: Student stops after finding the slope of line p and forgets the word perpendicular.
Option B: −1/9 ❌
Trap: Student takes the reciprocal but forgets to change the sign.
Option D: 9 ❌
Trap: Student removes the negative sign but does not take the reciprocal.
🧮 DESMOS CONFIRMATION
1. Open Desmos
2. Enter: 2y + 18x = 9
3. Enter: y = (1/9)x
4. Observe the lines intersect at a right angle
✔ Confirms slope of line
13th Question
Question: What is the value of ?
A)
B)
C)
D)
✅ Understand the QUESTION — Trigonometry & Periodicity
Question Explained
You are asked to find:
📐 Important Rules
1. What the Question Is Really Asking
You are asked to find the cosine of a very large angle measured in radians.
The trick is not to calculate it directly, but to use a fundamental trigonometric rule about cosine.
2. Cosine Period
What this means (plain English):
~ The cosine graph repeats itself every 2π.
~ After a full rotation around the circle, cosine comes back to the same value.
~ So angles that differ by all have the same cosine.
Why 2π?
~ A full circle = 360°
~ In radians, 360° = 2π
~ So cosine “resets” every
This is called the period of cosine, and:
Why Are We Allowed to Use Here?
Your angle is:
This is way larger than 2π, meaning the angle has gone around the circle many times.
👉 Instead of tracking every rotation, we remove full circles using multiples of .
3. Reduce the Angle
Convert to a standard angle between 0 and 2π.
4. Unit Circle Exact Values
From the unit circle:
| Angle | |
|---|---|
| 1 | |
| 0 |
These are memorized facts, not calculated.
🧠 Step-by-Step Solution
Since:
Divide:
So:
If you think, why did we make this:
then let’s revert it back to understand.
That is why, both are the same. If you think, why did we use 47, because above notice, we calculated 47 remainder 1, means and remainder .
Thus:
That is WHY
And:
Why is ?
Unit Circle Explanation (Visual Logic)
~ On the unit circle, cosine is the x-coordinate
~ At (30°), the point is: (x, y)
So:
This comes from a 30-60-90 triangle:
| Side | Value |
|---|---|
| Hypotenuse | 1 |
| Adjacent (cos) | |
| Opposite (sin) |
✅ Correct Answer: Option C
❌ Why Other Options Are Incorrect
1/2 → It is the result of cosine of or sine of
1 → cosine of 0
→ impossible (cosine ≤ 1)
⚠️ SAT Trap: not reducing the angle before evaluating cosine.
🧮 Desmos Trick
1. Type: cos(565π/6)
2. Type from 2nd line all the options one-by-one: sqrt3 / 2
3. Observe: The Option C will show the same as the question.
4. Output: 0.8660…
It means Option C is correct.
14th Question
Question:
Which ordered pair is a solution to the given (x, y) system of equations?
A) (0, 0)
B) (0, 4)
C) (8, 44)
D) (8, 84)
MATHEMATICAL SOLUTION (CORE LOGIC)
A point is a solution to a system only if it satisfies both equations at the same time.
Since both equations equal y, the logical move is to set them equal to each other.
This step is chosen because both expressions represent the same y-value.
Now simplify:
Subtract 4 from both sides:
Divide both sides by 5:
Rearrange:
Factor:
So:
Now find the corresponding y-values.
For
Let’s pick:
When x is 0, y will be 4.
Point: (0, 4)
For :
When x is 1, y will be 9.
Point: (1, 9) → not in options
But (0, 4) is in Option B.
❌ (0, 0)
Trap: Assuming origin works by default
~ Plug in x = 0 → y should be 4, not 0
~ Fails both equations
❌ (8, 44)
Trap: Checking only the linear equation
~ 5(8) + 4 = 44 ✔
~ But ❌
~ Fails quadratic equation
❌ (8, 84)
Trap: Incorrect squaring or mental math
~ Neither equation gives y = 84 for x = 8
Fails both
REAL DESMOS METHOD
1. What to type in Desmos:
y = 5x + 4
y = 5x^2 + 4
2. What Desmos shows:
~ A line and a parabola
~ Their intersection points are the solutions
Click the intersection:
~ Desmos shows (0, 4) and (1, 9)
Only (0, 4) appears in the options.
✔ This directly confirms the algebra.
15th Question
Question: f(x) = 39
For the given linear function 𝑓, which table gives three values of 𝑥 and their corresponding values of 𝑓(𝑥)?
A)
| 0 | 0 |
| 1 | 0 |
| 2 | 0 |
B)
| 0 | 39 |
| 1 | 39 |
| 2 | 39 |
C)
| 0 | 0 |
| 1 | 39 |
| 2 | 78 |
D)
| 0 | 39 |
| 1 | 0 |
| 2 | -39 |
Choice B is correct.
🧮 Step-by-Step Solution
The function:
means:
~ The output is always 39
~ It does not depend on x
~ The graph is a horizontal line
So for any value of x:
That includes:
Step: Evaluate explicitly
✅ Correct Answer: B)
Option A ❌
Trap: Student assumes constant function means zero output.
Option C ❌
Trap: Student incorrectly multiplies:
instead of
Option D ❌
Trap: Student assumes the function changes sign with x.
🧮 DESMOS CONFIRMATION
1. Open Desmos
2. Type: y = 39
3. Click Table
4. Enter: x = 0, 1, 2
5. All outputs show: 39
✔ Confirmed
16th Question
Question: The population density of Iceland, in people per square kilometer of land area, increased from 2.5 in 1990 to 3.3 in 2014. During this time period, the land area of Iceland was 100,250 square kilometers. By how many people did Iceland’s population increase from 1990 to 2014?
A) 330,825
B) 132,330
C) 125,312
D) 80,200
Question Understanding
The problem gives population density (people per square kilometer) at two different years and a fixed land area.
You are asked to find how many people the population increased by.
So this is: Population = Density × Land Area
Important Formula / Rule
Population increase:
Step-by-Step Solution
Step 1: Find the change in population density
New density – Old density
Step 2: Multiply by land area
Difference in density multiplied by Area:
Correct Answer: Option D
Why Other Options Are Wrong
330,825 → uses full density instead of the increase
132,330 → arithmetic mistake
125,312 → random incorrect multiplication
Common Student Mistake
❌ Calculating total population instead of population increase
Desmos Trick
In Desmos: (3.3 – 2.5) * 100250
17th Question
Question: The ratio 140 to is equivalent to the ratio 4 to 28. What is the value of ?
A) 112
B) 114
C) 980
D) 3,290
Question Understanding
You are given two equivalent ratios and must find the missing value .
Important Rule
Equivalent ratios ⇒ cross multiplication
Step-by-Step Solution
Step 1: Simplify the known ratio
Step 2: Set ratios equal
Step 3: Cross multiply
Correct Answer: Option C
Why Other Options Are Wrong
112 → incorrect scaling
144 → unrelated value
3,920 → multiplied instead of dividing
Common Student Mistake
❌ Not simplifying ratios before solving
Desmos Trick
1. Type: 140 / x = 4 / 28
~ Desmos will not understand m. It only gets x and y.
2. Check the graph: Zoom out if you are too zoomed in.
~ You will see a straight line on x = 980.
~ That is your answer.
18th Question
Question: The function is defined by . The graph of in the -plane has an -intercept at (, 0) and a-intercept at (0, ), where and are constants. What is the value of ?
A) 21
B) 28
C) 32
D) 35
Choice A is the correct answer.
🧮 Step-by-Step Solution
We are asked for a + b, so we must find:
~ the x-intercept value
~ x-intercept (, 0) = (x1, x2)
~ the y-intercept value
~ y-intercept (0, ) = (y1, y2)
~ the graph y = h(x)
Both intercepts come directly from the equation , (y = mx + b) but each intercept is found differently, so we must handle them one at a time.
Step 1: Find the y-intercept
Let’s pick up (x2 and y2)
~ x2 = 0
~ y2 =
By definition, the y-intercept occurs where:
Substitute into the function: y = 4x + 28
So:
Step 2: Find the x-intercept
Let’s pick up (x1 and y1)
~ x1 =
~ y1 = 0
By definition, the x-intercept occurs where:
Set the function equal to 0: y = 4x + 28
Subtract 28 from both sides:
Divide both sides by 4 or move 4 to left-hand side into divide form:
So:
Step 3: Compute
✅ Correct Answer: 21
Option B: 28 ❌
Trap: Student finds only the y-intercept and forgets the x-intercept.
Option C: 32 ❌
Trap: Student adds instead of intercept values.
Option D: 35 ❌
Trap: Student uses instead of , ignoring the negative sign.
🧮 DESMOS CONFIRMATION
1. Open Desmos
2. Type: y = 4x + 28
3. Click the x-intercept → shows
4. Click the y-intercept → shows
5. ✔ Confirms ,
19th Question
Question: Residents of a town were surveyed to determine whether they are satisfied with the concession stand at the local park. A random sample of 200 residents was selected. All 200 responded, and 87% said they are satisfied. Based on this information, which of the following statements must be true?
I. Of all the town residents, 87% would say they are satisfied with the concession stand at the local park.
II. If another random sample of 200 residents were surveyed, 87% would say they are satisfied.
A) Neither
B) I only
C) II only
D) I and II
Question Understanding
This question tests what can and cannot be concluded from a random sample.
~ Sample size = 200
~ Sample result = 87% satisfied
Important Statistical Rule
A sample percentage:
~ Estimates the population
~ Does not guarantee exact population results
~ Will vary from sample to sample
Evaluate Each Statement
Statement I: Of all town residents, 87% are satisfied.
❌ Not guaranteed
~ Sample ≠ entire population
~ Because they only selected 200 people, there could be more.
Statement II: Another sample of 200 would give exactly 87%.
❌ Not guaranteed
~ Sampling variability exists
~ If the question did not say anything about Another sample, we cannot assume ourselves.
Correct Answer: Option A
Why Other Choices Are Wrong
I only → assumes certainty from a sample
II only → ignores random variation
I and II → both false
Common Student Mistakes
❌ Treating sample results as exact population values
❌ Forgetting randomness causes variation
20th Question
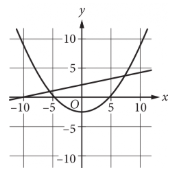
Question: A system of equations consists of a quadratic equation and a linear equation. The equations in this system are graphed in the xy-plane above. How many solutions does this system have?
A) 0
B) 1
C) 2
D) 3
🧠 Core Concept (What “solution” means here)
A solution to a system =
👉 a point where both graphs intersect
So:
~ Each intersection point = one solution
~ We are counting intersection points, not roots
🔍 Step-by-Step Graph Analysis (Why this works)
From the graph:
~ The curve is a parabola opening upward
~ The straight line cuts through the parabola
Now observe carefully:
~ The line intersects the parabola twice
~~ once on the left side
~~ once on the right side
These are two distinct intersection points.
✅ Correct Answer: 2
0 ❌
Trap: Student thinks line never touches parabola.
1 ❌
Trap: Student only notices one intersection and misses the second.
3 ❌
Trap: Student assumes vertex also counts as intersection (it doesn’t).
21th Question
Question: Jennifer bought a box of Crunchy Grain cereal. The nutrition facts on the box state that a serving size of the cereal is cup and provides 210 calories, 50 of which are calories from fat. In addition, each serving of the cereal provides 180 milligrams of potassium, which is 5% of the daily allowance for adults. If percent of an adult’s daily allowance of potassium is provided by servings of Crunchy Grain cereal per day, which of the following expresses in terms of ?
A)
B)
C)
D)
Note: The question is made to confuse students, too many unnecessary information but we must focus on only useful ones like below.
✅ Understand the QUESTION
Percent, Unit Rate & Linear Relationship
Given information (from the nutrition label):
~ 1 serving provides 180 mg potassium
~ This equals 5% of an adult’s daily allowance
~ x = number of servings per day
~ p = percent of daily allowance from servings
Question:
Which expression gives in terms of ?
🧠 Step-by-Step Reasoning
Step 1: Understand what 5% means here
The key sentence is:
“each serving of the cereal provides 180 milligrams of potassium, which is 5% of the daily allowance”
This tells us directly:
~ 1 serving → 5%
~ This is a linear relationship, not exponential because we were not asked “How many Times” here.
Step 2: Scale up to servings
If:
~ 1 serving gives 5%
~ Then servings give:
✅ Correct Equation: Option B
p = 0.5x ❌
Confuses 5% with 0.5%.
SAT trap: decimal misplacement.
p = ❌
Represents exponential decay, which is incorrect.
Potassium accumulates additively.
p = ❌
Represents compound growth.
SAT trap: mistaking repeated addition for exponential growth.
22th Question
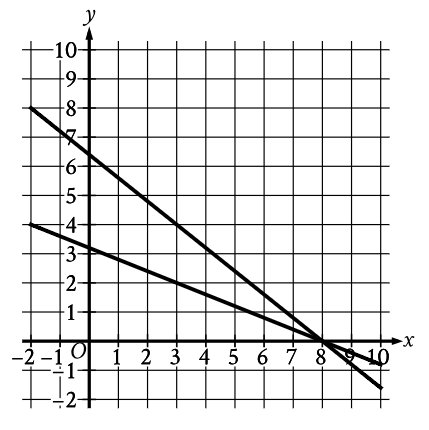
Question: What system of linear equations is represented by the lines shown?
A) 8x + 4y = 32
-10x – 4y = -64
B) 4x + 10y = 32
-8x – 10y = -64
C) 4x – 10y = 32
-8x + 10y = -64
D) 8x – 4y = 32
-10x + 4y = -64
Option B: (Graph shows two decreasing straight lines intersecting at the x-axis around )
🔍 Step-by-Step Graph Analysis
From the graph, we clearly observe:
• Both lines are sloping downward (negative slope)
• The two lines intersect exactly on the x-axis
• The point of intersection is approximately (x, y) = (8, 0)
• One line is steeper than the other
• The y-intercepts look close to 3–4 for one line and 6–7 for the other
So the correct system must satisfy all of these features.
🧮 Check Option B Carefully (Why It Works)
Method 1:
Equation 1: 4x + 10y = 32
Convert to slope-intercept form: 10y = −4x + 32
y = -4x + 32 divided by 10
y = −0.4x + 3.2
• Negative slope ✔
• y-intercept ≈ 3.2 ✔
• Matches the lower line in the graph ✔
Equation 2: −8x − 10y = −64
Multiply by −1: 8x + 10y = 64 (This step is optional)
Solve for y: 10y = −8x + 64
y = −0.8x + 6.4 divided by 10
y = −0.8x + 6.4
• Negative slope ✔
• Steeper than the first line ✔
• y-intercept ≈ 6.4 ✔
Intersection Check (CRITICAL)
Set equations equal:
y of Equation 1 = y of Equation 2
You can choose any equation to find out x. The x will be the same.
−0.4x + 3.2 = −0.8x + 6.4
The x value matches to the graph, now let’s check y as well.
Method 2: The Quickest Method (Use this when only one value is exactly the same in both like here 10y)
4x + 10y = 32
-8x – 10y = -64
The x value matches to the graph, now let’s check y as well.
Substitute : Now let’s try to fill the value of x and confirm the value of y. Again, the answer will be the same in both equation. For now, we are picking Equation 1.
y = -0.4x + 3.2
y = −0.4(8) + 3.2
y = -3.2 + 3.2
y = 0
✔ Intersection point = (8, 0)
✔ y-intercepts are 3.2 and 6.4 → graph also shows this, something between (3-4) and (6-7)
✔ Exactly matches the graph
✅ Option B is correct
Option A ❌
First equation: 8x + 4y = 32
⇒ 4y = -8x + 32
⇒ y = -8x + 32 divided by 4
⇒ y = −2x + 8
[If you calculate like above, the value of x will be: x = 4. It doesn’t match with the graph. It is incorrect, but if you still want to try for knowledge then continue.]
Second equation: −10x − 4y = −64
⇒ -4y = 10x – 64
⇒ y = 10x – 64 divided by -4
(If in doubt, how to divide then look above the “Without Optional Step.”)
⇒ y = −2.5x + 16
[Here the x will be: x = 6.4. Based on graph, the x should be 8.]
[All you need to do is find x value then calculate y, just like above. The same steps like Option B.]
• y-intercepts are 8 and 16 → graph does NOT show this (
• x is 4 and 6.4 → graph does NOT show this
• y is 0, matches with graph but without x. It is incorrect.
• Slopes are too steep
• Intersection is NOT at (8, 0)
❌ Rejected
Option C ❌ It is a Trap.
Equation 1: 4x − 10y = 32
⇒ y = 0.4x − 3.2
[Here x-intercept is 8. Calculate x like Option B. Let’s find out y.]
y = 0.4(8) – 3.2
⇒ y = 3.2 – 3.2
⇒ y = 0
(Since the Equation 1 matches with the graph, let’s confirm by checking Equation 2, because both should give the same value.)
Equation 2: -8x + 10y = -64
⇒ y = 0.8x – 6.4
[Here x-intercept is 8. Calculate x like Option B. Let’s find out y.]
⇒ y = 0.8(8) – 6.4
⇒ y = 6.4 – 6.4
⇒ y = 0
⚠️ Same as Option B
The REAL Deciding Factor (This Is the Key Point)
The question is NOT: “Which system intersects at (8, 0)?” (If it was then we focus on final values.)
The question is: “Which system matches the LINES SHOWN?”
That means we must match:
– intersection
– direction of slope
– orientation of the lines
From the EQUATION (Algebra Rule): y = mx + b
Option B – Both equations are -0.4x + 3.2 = -0.8x + 6.4
m = -0.4 (Equation 1), -0.8 (Equation 2)
📌 Both slopes are NEGATIVE (The definition of Negative slope: as x increases, y decreases.)
📌 Lines go downward left to right
📌 Exactly matches the graph
Option C – Both equations are 0.4x – 3.2 = 0.8x – 6.4
m = 0.4 (Equation 1), 0.8 (Equation 2)
📌 Both slopes are POSITIVE
📌 Lines go upward left to right
📌 This is the OPPOSITE of the graph
❌ Rejected
Option D ❌
Equation 1: 8x − 4y = 32
⇒ y = 2x − 8
[Here x-intercept is 4. Calculate x like Option B. Since it is clearly incorrect but still let’s find out y.]
y = 2(4) – 8
⇒ y = 8 – 8
⇒ y = 0
(The Equation 1 doesn’t match with the graph.)
• Positive slope
• Does not match graph direction
❌ Rejected
Memory rule for students: On graph if
Left high → right low = negative slope
Left low → right high = positive slope
The sign of m decides direction: y = mx + b
Slope (m) is Positive (+) = Line direction (Upward left → right)
Slope (m) is Negative (−) = Line direction (Downward left → right)
🧮 DESMOS CALCULATOR — EXACT SAT METHOD
Step-by-Step in Desmos
1. Open Desmos Calculator
2. In Expression Line 1, type: 4x + 10y = 32
→ Desmos automatically graphs the line
3. In Expression Line 2, type: -8x – 10y = -64
4. Click on the intersection point shown on the graph
→ Desmos displays: (8, 0)
5. Zoom in using mouse scroll / zoom buttons
6. Confirm:
– Both slopes go downward
– One line is steeper
– Intersection lies exactly on x-axis
✅ Desmos confirms Option B
Did you try all the features and get comfortable using them? You should work on using the calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes easier to learn and progress. You must try to work on your speed and spend less time on the beginning and more on the later questions. This is the SAT 2025 Practice Test of Math Module 1st.
There are more tests available:
- SAT 2025 Test (Math Module 2nd)
- SAT Test 5th (Math Module 2nd)
- SAT Test 4th (Reading and Writing Module 1st)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


