SAT Math Module 2nd (How to Get 1500+ Hack, Free Test 2024

Question: If $f(x) = \frac{x^2 – 6x + 3}{x – 1}$, what if $f(-1)$?
A) -5
B) -2
C) 2
D) 5

1️⃣ Explain the Question (What is being asked)
~ You are given a rational function
~ You must substitute x = −1 into the function
~ Since the denominator is not zero at $x = -1$, direct substitution is allowed

3️⃣ Step-by-Step Solution
The questions says:
$f(x) = \frac{x^2 – 6x + 3}{x – 1}$

where $f(x) = f(-1)$

Substitute $x = -1$: All we need to do is to fill the value x.

$f(-1) = \frac{(-1)^2 – 6(-1) + 3}{(-1) – 1}\\ \\f(-1) = \frac{(-1)^2 – 6(-1) + 3}{-1 – 1}$

Numerator:$$(-1)^2 – 6(-1) + 3 = 1 + 6 + 3 = 10$$
Denominator:$$-1 – 1 = -2$$
Final value:$$f(-1) = \frac{10}{-2} = -5$$

✅ Correct Answer: Option A

❌ -2 → Divided incorrectly
❌ 2 → Ignored sign of denominator
❌ 5 → Forgot denominator was negative

5️⃣ Desmos ACTUAL Trick
1. Type: f(x) = (x^2 – 6x + 3)/(x -1)
2. Type on the 2nd line: f(-1)
2. Desmos shows Output: -5

Question: A veterinarian recommends that each day a certain rabbit should eat 25 calories per pound of the rabbit’s weight, plus an additional 11 calories. Which equation represents this situation, where $c$ is the total number of calories the veterinarian recommends the rabbit should eat each day if the rabbit’s weight is $x$ pounds?
A) $c = 25x$
B) $c = 25x + 11$
C) $c = 36x$
D) $c = 11x + 25$

✅ Correct Answer: B) $c = 25x + 11$

🧮 Step-by-Step Correct Reasoning
The statement has three parts:
1. The weight is x and the 25 calory should be given according to weight, so we multiply.
2. 25 calories per pound → $25x$
3. Plus an additional 11 calories → $+ 11$
Combine both:
$$c = 25x + 11$$
✔ Matches Option B exactly

❌ Option A: $c = 25x$
Why students choose it:
They stop reading after: “25 calories per pound”
They ignore: “plus an additional 11 calories”
❌ Missing constant term

❌ Option C: $c = 36x$
Why students choose it:
They incorrectly add:
$$25 + 11 = 36$$
But 11 is not per pound, it’s a fixed amount.
❌ Mixed unit mistake

❌ Option D: $c = 11x + 25$
Why students choose it:
They reverse roles:
~ Treat 11 as “per pound”
~ Treat 25 as constant
This directly contradicts the wording.
❌ Misreading variables

🧮 DESMOS CALCULATOR — QUICK CHECK
Step-by-Step
1. Open Desmos
2. Type: c = 25x + 11
3. Use the Table icon
4. Try $x = 1$:
~ Calories = 36
~ Matches: 25 + 11
✔ Confirms equation logic

Question:
$f(x) = 2(3^x)$
For the function $f$ defined above, what is the value of $f(2)$?
A) 9
B) 12
C) 18
D) 36

1️⃣ Explain the Question
~ This is an exponential function
~ You substitute $x = 2$
~ Exponents must be evaluated before multiplication

2️⃣ Formula / Rule Used
Order of Operations (PEMDAS)
Exponents → Multiplication

3️⃣ Step-by-Step Solution
We know $f(x) = f(2)$, so
Substitute $x = 2$:$$f(2) = 2(3^2)$$
Calculate exponent:$$3^2 = 9$$
Multiply: $2(9)$$$2 \times 9 = 18$$
$f(2) = 18$
✅ Correct Answer: Option C

❌ 9 → Forgot to multiply by 2
❌ 12 → Multiplied before exponent
❌ 36 → Squared 6 incorrectly

5️⃣ Desmos ACTUAL Trick
We know x = 2, so
1. Type: 2(3^2)
2. Output: 18

Question: For the exponential function $f$, the value of $f(0)$ is $c$, where $c$ is a constant. Of the following equations that define the function $f$, which equation shows the value of $c$ as the coefficient or the base?
A) $f(x) = 22(1.5)^{x+1}$
B) $f(x) = 33(1.5)^x$
C) $f(x) = 49.5(1.5)^{x-1}$
D) $f(x) = 74.25(1.5)^{x-2}$

1️⃣ What the Question Is Really Testing
~ This is about the y-intercept of an exponential function
~ The y-intercept occurs when: $f(x) = f(0)$$$x = 0$$
So:$$f(0) = c$$
$c$ is Constant and coefficient or the base value.
The question is asking:
In which equation is the value of $f(0)$ already visible without doing extra exponent work?

2️⃣ Key Rule / Formula
For an exponential function:$$f(x) = a(b)^x$$
When $x = 0$:$$f(0) = a(b)^0 = a$$
✅ The coefficient a equals the y-intercept

3️⃣ Step-by-Step Option Analysis
The question tells us that the value of $f(x) = f(0) = c$
It gives us a clean hint that $x = 0$

But the most important hint is:
$c$ is Constant and coefficient or the base value.
~ In simple words, $c$ is the Initial value, so based on formula above: $c = a$
~ $a$: According to the formula, $a$ is the base value.

Overall what it means that the Base value is the Final value, so the solution is:
$a$ value is the answer.
Now look up the Options, which option do you consider stay remained?

Option B: $$f(x) = 33(1.5)^x$$
To Test – Substitute $x = 0$:
$$f(0) = 33(1.5)^0 = 33$$
✅ The coefficient directly equals c
✔ No extra calculation needed
✔ $a = c$ or Base Value Remains the same at last
✔ $a = 33$ and $c = 33$

Option A$$f(x) = 22(1.5)^{x+1}$$
Substitute $x = 0$:$$f(0) = 22(1.5)^1 = 33$$
❌ The value of $c$ is not shown directly
❌ $a$ and $c$ are not the same or Base Value doesn’t remain the same at last.
❌ $a = 22$ and $c = 33$.

Option C$$f(x) = 49.5(1.5)^{x-1}$$
Substitute $x = 0$:$$f(0) = 49.5(1.5)^{-1}$$
$f(0) = 49.5 \times (\frac{1}{1.5})^1\\ \\f(0) = \frac{49.5}{1.5}\\ \\f(0) = 33$

❌ The value of $c$ is not shown directly
❌ $a$ and $c$ are not the same or Base Value doesn’t remain the same at last.
❌ $a = 49.5$ and $c = 33$.

Option D$$f(x) = 74.25(1.5)^{x-2}$$
Substitute $x = 0$:$$f(0) = 74.25(1.5)^{-2}$$
$f(0) = 74.25 \times (\frac{1}{1.5})^2\\ \\f(0) = \frac{74.25}{2.25}\\ \\f(0) = 33$

❌ The value of $c$ is not shown directly
❌ $a$ and $c$ are not the same or Base Value doesn’t remain the same at last.
❌ $a = 74.25$ and $c = 33$.

Use Desmos as a calculator for this.

Question: Which of the following expressions is equivalent to $8x^{10} – 8x^9 + 88x$?
A) $x(7x^{10} – 7x^9 + 87x)$
B) $x(8^{10} – 8^9 + 88)$
C) $8x(x^{10} – x^9 + 11x)$
D) $8x(x^{9} – x^8 + 11)$

1️⃣ Explain the Question (Interpretation)
~ You are given a polynomial with three terms
~ The question asks for an equivalent expression
~ This usually means factoring, not expanding
~ Look for a common factor across all terms

2️⃣ Formula / Rule Used
Greatest Common Factor (GCF)
If all terms share a factor, factor it out:
$$ab + ac = a(b + c)$$

3️⃣ Step-by-Step Solution
Given:$$8x^{10} – 8x^9 + 88x$$
Step 1: Find the GCF
Coefficients: 8x¹⁰ – 8x⁹ + 88x
GCF of 8, 8, 88 → 8
Variables: smallest power of $x$ → x
So GCF = 8x

Step 2: Factor out 8x$$8x^{10} ÷ 8x = x^9$$$$-8x^9 ÷ 8x = -x^8$$$$88x ÷ 8x = 11$$
Final factored form:$$\boxed{8x(x^9 – x^8 + 11)}$$
✅ Correct Answer: Option D

❌ Option A:$$x(7x^{10} – 7x^9 + 87x)$$
~ Coefficients are changed incorrectly
~ Factoring never changes values

❌ Option B:$$x(8^{10} – 8^9 + 88)$$
~ Powers are wrongly applied to 8 instead of x
~ Completely different expression

❌ Option C:$$8x(x^{10} – x^9 + 11x)$$
~ Incorrect division while factoring
~ Inside powers increase instead of decrease

5️⃣ Desmos ACTUAL Trick
1. Type the question equation: 8x^10 – 8x^9 + 88x
2. Check the graph: You will see line.
3. Type Options one-by-one in different lines.
4. Observe:
~ Both Question and Option D overlaps perfectly. They are on the same track.
That confirms our correct option.

Question:
𝑦 = 2𝑥 + 10
𝑦 = 2𝑥 − 1
At how many points do the graphs of the given equations intersect in the xy-plane?
A) Zero
B) Exactly one
C) Exactly two
D) Infinitely many

🧠 Core Concept Used
Lines intersect once if slopes are different
Lines never intersect if:
~ Slopes are the same
~ Intercepts are different

🧮 Step-by-Step Solution
The formula: $y = mx + b$
Step 1: Compare slopes
Both equations have slope:
$$m = 2$$
So the lines are parallel.

Step 2: Compare y-intercepts
First line: $b = 10$
Second line: $b = -1$
Different intercepts → different lines

Step 3: Conclusion
Parallel lines never intersect.
✅ Correct Answer: Zero

Option B: Exactly one ❌
Trap: Student assumes all linear systems intersect once.

Option C: Exactly two ❌
Trap: Student confuses with quadratic intersections.

Option D: Infinitely many ❌
Trap: Would only occur if equations were identical.

🧮 Desmos Confirmation
Plot:
y = 2x + 10
y = 2x – 1
✔ Parallel lines, no crossing

Question: The expression $90y^5 – 54y^4$ is equivalent to $ry^4(15y – 9)$, where $r$ is a constant. What is the value of $r$?
A) 6
B) 9
C) 15
D) 90

1️⃣ What the Question Is Testing
~ This is factoring
~ You must match coefficients
~ The structure:$$ry^4(15y – 9)$$
~ $90y^5 – 54y^4\ =\ ry^4(15y – 9)$

2️⃣ Step-by-Step Factoring
Start with:$$90y^5 – 54y^4$$
Factor out the greatest common factor:
~ GCF of 90 and 54 → 18
~ Lowest power of $y$ → $y^4$$$90y^5 – 54y^4 = 18y^4(5y – 3)$$
Now rewrite the given expression:$$ry^4(15y – 9)$$
Factor inside:$$15y – 9 = 3(5y – 3)$$
So:$$ry^4(15y – 9) = 3r y^4(5y – 3)$$

3️⃣ Match the Coefficients
From factoring:$$18y^4(5y – 3)$$
From rewritten form:$$3r y^4(5y – 3)$$
So:$$3r = 18$$
Solve:$$r = 6$$
✅ Correct Answer: Option A

Choice B is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

🧮 Desmos Trick
1. Type: x = 90y^5 – 54y^4
2. Do not directly type: ry^4(15y – 9)
3. What we need to do is to put value of $r$:
~ The options are values of $r$
~ So replace it with 6, 9, 15, 90.
~ Type in 2nd line like this: x = 6y^4(15y – 9)
4. Observe:
~ The graph lines overlap – confirms correctness of the Option.

Question: A rectangular volleyball court has an area of 162 square meters. If the length of the court is twice the width, what is the width of the court, in meters?
A) 9
B) 18
C) 27
D) 54

1️⃣ Explain the Question
~ Rectangle area is given
~ Relationship between length and width is given
~ We are solving for width
~ This is a systems / substitution word problem

2️⃣ Formula / Rule Used
Area of a Rectangle$$A = l \times w$$
Area of Rectangle: $A$
Length = $l$
Width = $w$

3️⃣ Step-by-Step Solution
Let:
~ Width = $w$
~ Length = $2w$ (Question told: If the length is twice the width)
Substitute into area formula: $A = l \times w$
We know that $l = 2w$
$$162 = 2w \cdot w$$$$162 = 2w^2$$
Divide by 2 both sides or just move 2 to left-hand side in divide position:
$$w^2 = 81$$
Take square root: $w = \sqrt{81}$$$w = 9$$
✅ Correct Answer: Option A

❌ 18: Student forgot to square root
❌ 27: Multiplied instead of solving
❌ 54: Treated area as perimeter

5️⃣ Desmos ACTUAL Trick
1. Type in Desmos: 2w^2 = 162
2. Desmos solves: w = 9
But if you want to see visually in graph then
1. Type: y = 2x^2
2. Type in 2nd line: y = 162
3. Observe: The graph Intersection at x = 9.

Question: In right triangle $RST$, the sum of the measures of angle $R$ and angle $S$ is 90 degrees. The value of $sin(R)$ is $\frac{\sqrt{15}}{4}$. What is the value of $cos(S)$?

A) $\frac{\sqrt{15}}{15}$

B) $\frac{\sqrt{15}}{4}$

C) $\frac{4\sqrt{15}}{15}$

D) $\sqrt{15}$

✅ Understand the QUESTION
Trigonometry: Complementary Angles
Given:
~ Triangle RST is a right triangle
$\angle R + \angle S = 90^\circ$
That means R and S are complementary angles

$\sin(R) = \dfrac{\sqrt{15}}{4}$
Asked:
Find $\cos(S)$

🧠 Key Trigonometry Rule
In a right triangle:$$\sin(\theta) = \cos(90^\circ – \theta)$$
Since:$$S = 90^\circ – R$$
Go back to the definitions (this is the real “why”)
In a right triangle:$$\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}$$$$\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}$$
Now look at angles R and S:
What is opposite to R → is adjacent to S
What is adjacent to R → is opposite to S
So the same two sides are used — just swapped roles.
That’s why:$$\cos(S) = \sin(R)$$

Step 1: Core Trigonometric Rule Used
For complementary angles in a right triangle:
~ Let’s understand why $cos(S) = sin(R)$ are the same.
~ The question tells us: $\angle R + \angle S = 90 \degree$
~ That means $\angle R = 90 \degree – \angle S$, and $\angle S = 90 \degree – \angle R$
So: $sin(R) = cos(90\degree – R)$ and $cos(S) = sin(90\degree – S)$
That is why:
$sin(R) = cos(S)$ → $sin(R) = cos(90\degree – R)$,
so $cos(S) = cos(90\degree – R)$ → $S = 90\degree – R$

Do you get is now? For knowledge, you can check sin(S) too.
$cos(S) = sin(R)$ → $cos(S) = sin(90\degree – S)$,
so $sin(R) = sin(90\degree – S)$ → $R = 90\degree – S$

We know now that $S = 90\degree – R$

✏️ Apply the Rule to Understand
Look above “Go back to definition” part to better understand, why they are the same.
$$\cos(S) = \frac{\sqrt{15}}{4}$$
Direct complementary-angle identity.
Option B is correct.
If you are still not satisfied, take a Practical Visual Desmos test to understand better.

Option A:
Wrong ratio; unnecessary simplification.

Option C:
Reciprocal mistake.

Option D:
Trigonometric values must be ≤ 1.

📌 Concept Reminder
Sine of one acute angle equals cosine of the other in right triangles.

DESMOS Tricks
1. Type in one line: sin(x)
2. Type in second line: cos(90-x)
3. Observe:
~ The graphs overlap exactly
~ This visually proves: sin(R) = cos(S)

Question: The pressure exerted on a scuba diver at sea level is 14.70 pounds per square inch (psi). For each foot the scuba diver descends below sea level, the pressure exerted on the scuba diver increases by 0.44 psi. What is the total pressure, in psi, exerted on the scuba diver at 105 feet below sea level?
A) 60.90
B) 31.50
C) 14.70
D) 0.44

🧠 Core Concept (Why this is a linear model)
This situation has:
~ a starting value (pressure at sea level)
~ a constant rate of increase per foot
So we model it using:
$$\text{Total pressure} = \text{initial pressure} + (\text{rate})(\text{depth})$$

Choice B is correct.
🧮 Step-by-Step Solution
Step 1: Identify known values
~ Initial pressure = 14.70 psi
~ Rate of increase = 0.44 psi per foot
~ Depth = 105 feet

Step 2: Calculate pressure increase due to depth
This step is necessary because the increase happens every foot, not once: (Rate) $\times$ (Depth)
$$0.44 \times 105 = 46.20$$
This is the additional pressure caused by going down 105 feet.

Step 3: Add sea-level pressure (Initial)
The diver already experiences pressure at sea level, so we must add it.
$$14.70 + 46.20 = 60.90$$
✅ Correct Answer: A) 60.90

Option B: 31.50 ❌
Trap: Student multiplies incorrectly or uses half the depth.

Option C: 14.70 ❌
Trap: Student ignores depth entirely.

Option D: 0.44 ❌
Trap: Student mistakes rate for total pressure.

🧮 Desmos Confirmation
Type: 14.7 + 0.44(105)
✔ Output = 60.9

Question:
$s(n) = 38,000a^n$
The function $S$ above models the annual salary, in dollars, of an employee $n$ years after starting a job, where $a$ is a constant. If the employee’s salary increases by 4% each year, what is the value of $a$?
A) 0.04
B) 0.4
C) 1.04
D) 1.4

1️⃣ Explain the Question
~ This is an exponential growth model
~ $a$ represents the growth factor
~ A percent increase must be converted correctly

2️⃣ Formula / Rule Used
The main formula: $s(n) = I(1 + \frac{4}{100})^n$

But the question only asked to find growth, so: $(1 + \frac{4}{100})$
Growth Factor Rule
If something increases by $r\%$:$$\text{Growth factor} = 1 + r$$
$r$ is 4% or $\frac{4}{100}$

3️⃣ Step-by-Step Solution
Given:
~ Increase = 4%
~ Convert percent to decimal:$$4\% = 0.04$$
Apply rule:$$a = 1 + 0.04 = 1.04$$
✅ Correct Answer: Option C

❌ 0.04: Student forgot to add 1
❌ 0.4: Miscalculated percentage and forgot to add 1
❌ 1.4: Miscalculated percentage

Use DESMOS as a calculator for this.

Question: Which of the following is an equivalent form of $(1.5x – 2.4)^2 – (5.2x^2 – 6.4)$?
A) $-2.2x^2 + 1.6$
B) $-2.2x^2 + 11.2$
C) $-2.95x^2 – 7.2x + 12.16$
D) $-2.95x^2 – 7.2x + 0.64$

1️⃣ Key Algebra Rules Used
Square a binomial$$(a – b)^2 = a^2 – 2ab + b^2$$
~ Distribute negative sign
~ Combine like terms

2️⃣ Step-by-Step Expansion
Step 1: Square the binomial$$(1.5x – 2.4)^2$$$$= (1.5x)^2 – 2(1.5x)(2.4) + (2.4)^2$$$$= 2.25x^2 – 7.2x + 5.76$$
Step 2: Subtract the second expression$$– (5.2x^2 – 6.4) = -5.2x^2 + 6.4$$
Step 3: Combine like terms:
$2.25x^2 – 7.2x + 5.76 – 5.2x^2 + 6.4\\ \\ 2.25x^2 – 5.2x^2 -7.2x + 5.76 + 6.4$
$$2.25x^2 – 5.2x^2 = -2.95x^2$$$$-7.2x \text{ stays}$$$$5.76 + 6.4 = 12.16$$
Final expression:$$-2.95x^2 – 7.2x + 12.16$$
✅ Correct Answer: Option C

Choice A is incorrect and may result from conceptual or calculation errors.

Choice B is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

🧮 Desmos Trick
1. Type: y = (1.5x – 2.4)^2 – (5.2x^2 – 6.4)
2. Type from 2nd line all options one-by-one: y = -2.95x^2 – 7.2x + 12.16
3. Observe:
~ The graph lines overlap – confirms correctness of the Option.

Question: Square X has a side length of 12 centimeters. The perimeter of square Y is 2 times the perimeter of square X. What is the length, in centimeters, of one side of square Y?
A) 6
B) 10
C) 14
D) 24

✅ Understand the QUESTION
Perimeter of Squares
Given:
~ Square X has side length = 12 cm
~ Perimeter of square Y, 2 times X = 2 × perimeter of square X
Asked:
Side length of square Y

🧠 Key Geometry Formula$$\text{Perimeter of square} = 4 \times \text{side}$$

✏️ Step-by-Step Solution
Step 1: Perimeter of square X: 4 × side
4 × 12 = 48
Step 2: Perimeter of square Y: 2 × Square X
2 × 48 = 96
Step 3: Side of square Y:
A Square has 4 sides, so we divide it by 4 to get one side.
96 ÷ 4 = 24
✅ Correct Answer: Option D

6 ❌
Directly divide 12 by 2, don’t do it.

10 ❌
Directly subtract 2 from 12.

14 ❌
Directly add 2 to 12.

DESMOS Tricks
It is better to just use Desmos as a calculator for this one.

Question: The function $f$ is defined by $f(x) = 7x – 84$. What is the x-intercept of the graph of $y = f(x)$ in the xy-plane?
A) (-12, 0)
B) (-7, 0)
C) (7, 0)
D) (12, 0)

🧠 Core Concept (Why x-intercept means this)
The x-intercept is the point where: Take reference from options (x, y)
$$y = 0$$
So we must set the function equal to zero.

🧮 Step-by-Step Solution
Step 1: Set $f(x) = 0$
$$7x – 84 = 0$$
Step 2: Solve for $x$
Move add to right-hand side, which changes its sign from negative to positive:
$$7x = 84$$
Divide by 7:
$$x = 12$$
Step 3: Write as an ordered pair
$$(12, 0)$$
✅ Correct Answer: D) (12, 0)

Option A: (-12, 0) ❌
Trap: Student moves 84 to the wrong side and changes sign incorrectly.

Option B: (-7, 0) ❌
Trap: Student divides 84 by 12 instead of 7.

Option C: (7, 0) ❌
Trap: Student confuses coefficient with solution.

🧮 Desmos Confirmation
1. Type: y = 7x – 84
2. Look the graph
~ Graph crosses x-axis at x = 12

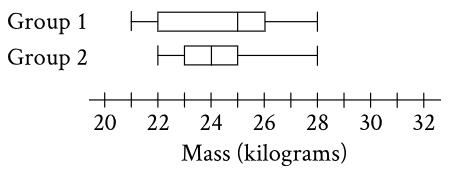
Question: The box plots summarize the masses, in kilograms, of two groups of gazelles. Based on the box plots, which of the following statements must be true?
A) The mean mass of group 1 is greater than the mean mass of group 2.
B) The mean mass of group 1 is less than the mean mass of group 2.
C) The median mass of group 1 is greater than the median mass of group 2.
D) The median mass of group 1 is less than the median mass of group 2.

1️⃣ What This Question Is Testing
This is SAT Data Analysis.
Key idea:
Box plots show medians and quartiles, NOT means.
So:
~ You can compare medians
~ You cannot determine means from a box plot alone

2️⃣ Critical Rules You Must Know
📌 Box Plot Facts
Median → vertical line inside the box
Mean → NOT shown
Statements about means cannot be guaranteed

3️⃣ Read the Box Plots Carefully
From the image:
~ Median of Group 1 is to the right of the median of Group 2
~ That means: $$\text{Median(Group 1)} > \text{Median(Group 2)}$$
4️⃣ Correct Answer Explained
✅ C) The median mass of group 1 is greater than the median mass of group 2
This is directly visible from the median lines.

5️⃣ Why the Other Options Are Wrong (REAL SAT TRAPS)
❌ A) Mean of group 1 > mean of group 2
❌ B) Mean of group 1 < mean of group 2
→ Means are not shown
→ Distribution shape can change the mean
→ SAT trick: never assume mean from a box plot
❌ D) Median of group 1 < median of group 2
→ Opposite of what the graph clearly shows

🧮 Desmos Note (Why It’s Not Used Here)
Desmos cannot compute medians from box plots unless raw data is given.
This question is visual reasoning, not computation.

Question: The function $f$ is defined by $f(x) = a(2.2^x + 2.2^b)$, where $a$ and $b$ are integer constants and $0 < a < b$. The functions $g$ and $h$ are equivalent to function $f$, where $k$ and $m$ are constants. Which of the following equations displays the $y$-coordinate of the $y$-intercept of the graph of $y = f(x)$ in the $xy$-plane as a constant or coefficient?
I. $g(x) = a(2.2^x + k)$
II. $h(x) = a(2.2)^x + m$
A) I only
B) II only
C) I and II
D) Neither I nor II

Understand the Question
The function: $f(x) = a(2.2^x + 2.2^b)$
~ where $a$ and $b$ are constant integer
~ and $0 < a < b$ ($a$ is bigger than value 0 and $b$ is bigger than $a$)

The functions $g$ and $h$ are equivalent to function $f$
~ where $k$ and $m$ are constants
it means $k = 2.2^b$ and $m = 2.2^b$

The graph of $y = f(x)$ in the $xy$-plane

I. $g(x) = a(2.2^x + k)$
II. $h(x) = a(2.2)^x + m$
Which equation displays the $y$-coordinate of the $y$-intercept as a constant or coefficient?

🧠 STEP 1: What the question is REALLY testing (critical)
The question is not asking:
~ which form is equivalent or
~ which form gives the y-intercept when substituted
It is asking something much stricter:
~ Does the equation visibly display the y-intercept as a constant or coefficient?
That means:
~ The y-intercept must be directly readable
~ Not hidden inside a parameter
~ Not requiring substitution or calculation
This distinction is where the trap is.

🧠 STEP 2: Find the actual y-intercept of $f(x)$
y-intercept occurs where:$$x = 0$$
Substitute into $f(x)$:$$f(0) = a(2.2^0 + 2.2^b)$$
The exponent 0 means 1:
$2.2^2 = 1 \times 2.2 \times 2.2\\ \\2.2^1 = 1 \times 2.2$
$2.2^0 = 1 \times$Nothing (Because of 0, when there is nothing, 1 left alone always)
$$2.2^0 = 1$$$$f(0) = a(1 + 2.2^b)$$
So the true y-intercept value is:$$\boxed{a + a(2.2^b)}$$
Keep this exact form in mind — everything is compared to this value.

🧠 STEP 3: Analyze Statement I CAREFULLY
I. $g(x) = a(2.2^x + k)$
Because $g$ is equivalent to $f$, we must have:$$k = 2.2^b$$
Now find the y-intercept of $g(x)$:$$g(0) = a(1 + k)$$
Substitute $k = 2.2^b$:$$g(0) = a(1 + 2.2^b)$$
✔ This equals the correct y-intercept value.

⚠ BUT HERE IS THE KEY POINT (SAT LOGIC):
~ The equation does NOT show $a + a(2.2^b)$ explicitly
~ The y-intercept is hidden inside the symbol $k$
~ You cannot read the y-intercept directly from the equation
~ If the I takes common then it will match exactly the same to the equation but “The question especially emphasis on Display part,” so we cannot choose it.

Since:
$k \neq a + a(2.2^b)$
$k$ is just a placeholder, not the intercept itself
❌ Statement I does NOT display the y-intercept as a constant or coefficient

🧠 STEP 4: Analyze Statement II (same strict logic)
II. $h(x) = a(2.2)^x + m$
Because $h$ is equivalent to $f$, we must have:$$m = a(2.2^b)$$
Now evaluate the y-intercept:$$h(0) = a(1) + m = a + a(2.2^b)$$
✔ This equals the correct y-intercept value.
⚠ But again — SAT precision matters:
~ The y-intercept is not shown directly
~ The constant $m$ equals only part of the intercept
~ The full intercept is $a + m$, not just $m$
So:
~ The equation does not explicitly display the y-intercept
~ You must still compute it
❌ Statement II also fails the requirement

🧠 STEP 5: Why “I and II” is WRONG (this is where I earlier erred
The earlier mistake was assuming:
“If substituting x = 0 gives the intercept, then it is displayed.”
That assumption is incorrect for this question.
The phrase “displays the y-coordinate as a constant or coefficient” means:
~ You should be able to see the y-intercept immediately
~ Without substitution
~ Without hidden parameters
~ Without algebra
~ Neither equation does that.
✅ CORRECT ANSWER: Option D$$\boxed{\text{Neither I nor II}}$$

Choice A seems possible but the word “Display” made it incorrect. The question is easy but it is a difficult category question, that means hidden keys. You must practice questions like these, so it won’t hinder your exam score.

Choice B is clearly incorrect, whether we talk about visual or equation, it never matches it

Choice C is also incorrect because II is clearly incorrect.

Question: Square A has side lengths that are 166 times the side lengths of square B. The area of square A is $k$ times the area of square B. What is the value of $k$?
A) 2
B) 166
C) 332
D) 27556

✅ Understand the QUESTION — Squares & Area Scaling
Given
~ Side of square A = 166 × side of square B
~ Area of square A = $k$ × area of square B
~ Find $k$

1️⃣ Key Rule (VERY IMPORTANT)
📌 Area Scaling Rule
If side length scales by factor $n$,$$\text{Area scales by } n^2$$

2️⃣ Step-by-Step Calculation
Side ratio:$$166$$
Area ratio:$$166^2 = 27556$$
✅ Correct Answer: Option D

❌ Why Other Options Are Wrong
❌ 2 → ignored scale completely
❌ 166 → linear scaling mistake
❌ 332 → doubled instead of squared
SAT loves squaring traps.

🧮 Desmos Trick (Legit Use)
Type: 166^2
Instant verification.

Question: A school district is forming a committee to discuss plans for the construction of a new high school. Of those invited to join the committee, 15% are parents of students, 45% are teachers from the current high school, 25% are school and district administrators, and the remaining 6 individuals are students. How many more teachers were invited to join the committee than school and district administrators?
A) 6
B) 8
C) 10
D) 18

✅ Understand the Question
Committee members:
~ 15% parents
~ 45% teachers
~ 25% administrators
~ Remaining = 6 students
How many more teachers than administrators were invited?

1️⃣ What the Question Is Testing
This is percent → total → comparison.
Key challenge:
The total number is NOT given directly — you must find it.

2️⃣ Step-by-Step Solution
Step 1: Add known percentages$$15\% + 45\% + 25\% = 85\%$$
So remaining:$$100\% – 85\% = 15\%$$
This 15% corresponds to 6 students. Because they are remaining.

Step 2: Find the total number invited$$15\% \rightarrow 6 \Rightarrow 1\% \rightarrow \frac{6}{15} = 0.4$$$$100\% \rightarrow 0.4 \times 100 = 40$$
Total invited = 40 people

Step 3: Find teachers and administrators
Teachers:$$45\% \times 40 = 18$$
Administrators:$$25\% \times 40 = 10$$
Step 4: Compare$$18 – 10 = 8$$
✅ Correct Answer: Option B
8 more teachers.

❌ Incorrect Options Explained
❌ 6 → forgot to convert percent to total
❌ 10 → confused administrators count with difference
❌ 18 → gave number of teachers, not the difference

🧮 Desmos Trick (REAL USE)
1. Calculate all percentage:
~ Type: 100 – (15 + 45 +25)
~ Output: 15
That is out 15% which is equal to 6 students.
2. Type: 6 * 100/15
→ gives 40
3. Then use teacher and administers percentage:
45 * 40/100
0.25 * 40/100
4. The output will be: 18 and 10
5. Find how many teachers are more than administers: 18 – 10
6. Output: 8
Fast and SAT-legal.

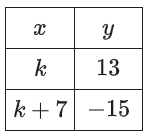
Question: The table gives the coordinates of two points on a line in the $xy$-plane. The $y$-intercept of the line is $(k – 5, b)$, where $k$ and $b$ are constants. What is the value of $b$?

[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

✅ Correct Answer: $b = 33$

🧮 Correct Solution — Step by Step
Step 1: Identify the two given points
From the table:
Point 1 (x₁, y₁): $(k,\,13)$
Point 2 (x₂, y₂): $(k+7,\,-15)$

Step 2: Find the slope of the line
Slope formula:
$$m = \frac{y_2 – y_1}{x_2 – x_1}$$
Substitute:$$m = \frac{-15 – 13}{(k+7) – k}$$
$$m = \frac{-28}{7}$$
$$m = -4$$
✔ Slope is −4

Step 3: Use slope to find the y-intercept
Use point-slope reasoning with point $(k, 13)$. Instead of using Point 1, you can also use Point 2.
Slope-intercept form:$$y = mx + b$$
Substitute values:$$13 = -4(k) + b$$
Solve for $b$:$$b = 13 + 4k$$

Step 4: Use the given y-intercept coordinate
The y-intercept is given as:$$(k – 5,\, b)$$
But y-intercept always has x = 0.
So:$$k – 5 = 0$$
$$k = 5$$
Step 5: Substitute $k = 5$ into $b = 13 + 4k$
$$b = 13 + 4(5)$$
$$b = 13 + 20$$
$$b = 33$$
✔ Correct value of $b$ is 33.

Trap 1: b = 13 ❌
How students get this:
They think: “The y-intercept must be one of the given y-values.”
But neither given point is at x = 0.
❌ Incorrect logic

Clarification
First, what is a y-intercept? (This matters for Step 4)
A y-intercept is: The point where the graph crosses the y-axis
This is not optional, not a formula trick — it is a definition.

CRITICAL FACT
On the y-axis, the x-coordinate is always 0.
Why?
Because:
~ The y-axis is the vertical line where x does not move left or right.
~ Any point on the y-axis has x = 0.
Examples:
~ (0, 5) → on the y-axis
~ (0, −3) → on the y-axis
~ (0, b) → y-intercept in general
If x ≠ 0, the point is not on the y-axis.

🧮 DESMOS CALCULATOR — CLEAN & FAST METHOD
Step-by-Step in Desmos
1. Open Desmos
2. Define points:
~ A = (5, 13)
~ B = (12, -15)
3. Type: y = -4x + b
4. Adjust b slider until the line passes through both points
5. Desmos shows: b = 33
✔ Visual confirmation

Question: If $\frac{\sqrt{x^5}}{\sqrt[3]{x^4}} = x^{\frac{a}{b}}$ for all positive values of $x$, what is the value of $\frac{a}{b}$?

[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

1️⃣ First: What is this “3”? Is it multiplied, divided, or something else?
That small 3 is NOT multiplication.
It is the index of the radical, meaning:
🔹 Rule$$\sqrt[n]{x^m} = x^{\frac{m}{n}}$$
So:
• Square root (a normal root like this $\sqrt{x^5}$) → index or $n$ is 2
• Cube root (a cube root like this $\sqrt[3]{x^4}$) → index or $n$ is 3

2️⃣ Why Do We Use $\frac{m}{2}$ or $\frac{m}{n}$ ?
Because radicals and exponents are equivalent forms.
Fundamental Identity:$$\sqrt[n]{x^m} = (x^m)^{1/n} = x^{m/n}$$
That’s why:
• Square root → power $\frac{1}{2}$
• Cube root → power $\frac{1}{3}$

3️⃣ Step-by-Step Solution
Rewrite Each Part Using Exponents
Numerator$$\sqrt{x^5} = x^{5/2}$$
Explanation:
• Square root = power $1/2$
• So exponent becomes $5 \times \frac{1}{2} = \frac{5}{2}$

Denominator$$\sqrt[3]{x^4} = x^{4/3}$$
Explanation:
• Cube root = power $1/3$
• So exponent becomes $4 \times \frac{1}{3} = \frac{4}{3}$

4️⃣ Divide Powers with the Same Base
We now have:$$\frac{x^{5/2}}{x^{4/3}}$$
Rule:
What Divide is actually: We subtract values in divide, right?
So:
$$\frac{x^m}{x^n} = x^{m-n}$$
Step-by-Step Subtraction
Convert to a common denominator:
$\frac{x^\frac{5}{2}}{x^\frac{4}{3}}\\ \\ x^{\frac{5}{2} – \frac{4}{3}}$

Take LCM of denominator 2 and 3: $\frac{5}{2} – \frac{4}{3}$
It is 6.
Now divide New LCM Denominator by Old denominators:
$6 \div 2 = 3\\ \\6 \div 3 = 2$

Multiply the value to its numerator:
$\frac{5 \times 3 – 4 \times 2}{6}$

Subtract:
$\frac{15 – 8}{6} \\ \frac{7}{6}$

5️⃣ Final Exponent$$x^{\frac{7}{6}}$$
$x^\frac{a}{b} = x^\frac{7}{6}$
So: $$\boxed{\frac{a}{b} = \frac{7}{6}}$$
✅ FINAL ANSWER: $\frac{7}{6}$ or $1.166$

⚠️ COMMON STUDENT MISTAKES (VERY IMPORTANT)
❌ Mistake 1: Treating the 3 as multiplication
Students think:$$\sqrt{3x^4}$$
❌ Completely wrong

❌ Mistake 2: Writing $\sqrt[3]{x^4} = x^{4/2}$
Wrong — index controls denominator

❌ Mistake 3: Dividing exponents instead of subtracting
They do:$$\frac{5/2}{4/3}$$❌ Illegal operation

❌ Mistake 4: Forgetting common denominator
Leads to wrong fraction like $\frac{1}{6}$

🧮 REAL DESMOS CHECK
You must know basic concepts. All the Hard questions requires your Mathematical knowledge. You should use Desmos only as a calculator.

Question: A sample of 40 fourth-grade students was selected at random from a certain school. The 40 students completed a survey about the morning announcements, and 32 thought the announcements were helpful. Which of the following is the largest population to which the results of the survey can be applied?
A) The 40 students who were surveyed
B) All fourth-grade students at the school
C) All students at the school
D) All fourth-grade students in the county in which the school is located

1️⃣ What This Question Is Testing
~ sample of 40 fourth-grade students
~ sample from one school
~ largest population

This is statistical inference.
Key SAT rule:
You can generalize results only to the population from which the sample was randomly selected.

2️⃣ Identify the Population
~ Sample: 40 fourth-graders
~ Location: one school
~ Random selection: within that school only

3️⃣ Correct Answer Explained
✅ B) All fourth-grade students at the school
Why?
~ Same grade
~ Same school
~ Same population source

4️⃣ Why Other Options Are Wrong
❌ A) Only the 40 students
→ Too narrow, 40 students of what / where (SAT wants the largest valid population)
❌ C) All students at the school
→ Includes other grades → not sampled
❌ D) All fourth-graders in the county
→ Different schools → not randomly sampled

🧮 Desmos Note
Desmos is not used here because:
~ No calculation required
~ This is a logic + sampling question

Question: Function $f$ is defined by $f(x) = -a^x + b$, where $a$ and $b$ are constants. In the $xy$-plane, the graph of $y = f(x) – 12$ has a $y$-intercept at $(0, -\frac{75}{7})$. The product of $a$ and $b$ is $\frac{320}{7}$. What is the value of $a$?

[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

✅ Understand the QUESTION
Question$$f(x) = -a^x + b$$
The graph of:$$y = f(x) – 12$$
has a y-intercept at:$$\left(0, -\frac{75}{7}\right)$$
Given:$$ab = \frac{320}{7}$$
Find $a$.

1️⃣ Key Concept
The y-intercept occurs when:$$x = 0$$

2️⃣ Step-by-Step Solution
Rather then first solving for $f(x)$ then put the value of $f(x)$ into the graph of y. It would be better that we directly put $f(x)$ into the equation like below:
Compute the y-Intercept Algebraically
Start with:$$y = -a^x + b – 12$$
Substitute $x = 0$:$$y = -a^0 + b – 12$$
Since:
$a^2 = 1 \times a \times a\\ \\a^1 = 1 \times a$

$a^0 = 1 \times$Nothing, so it leaves with 1 only. $a^0 = 1$

Put the value of 1 in the equation: $y = -1 + b – 12$
$y = b -1 – 12\\ \\y = b -13$

3️⃣ Use the Given y-Intercept: $(x, y) = (0, -\frac{75}{7})$

Put the value of y-intercept now
$-\frac{75}{7} = b – 13$
$$b – 13 = -\frac{75}{7}$$
Add 13 to both sides or just move -13 to right-hand side:
Let’s see both ways for educational purpose:

4️⃣ Use the Product Condition
We have b now and we need to find a
$$ab = \frac{320}{7}$$
Substitute $b$:$$a \cdot \frac{16}{7} = \frac{320}{7}$$
Multiply both sides by 7:
$\frac{16a}{7} \times 7 = \frac{320}{7} \times 7\\ \\16a = 320\\ \\ a = \frac{320}{16} \\ \\a = 20$

✅ Correct Answer: 20

❌ Typical Traps
• Forgetting to subtract 12
• Using $a^0 = 0$ instead of 1
• Mixing up intercept with asymptote

🧮 Desmos Confirmation
Use Desmos only for calculator, above you are given all steps, just understand them and crack it up.