
Solution of the SAT Math Test Question: Module 1st with Tricks to get 1560 Marks
Did you take the SAT Math Test 2 & 1? If yes, then you can your learning by taking the 3rd test. Like the other exams, it has the same exam format with all the necessary features for you to become a master in Math. You just take the SAT Test Module First to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after step-by-step explanations.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 1st.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 1ST
The first module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 1st are from easy to difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 1st. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH EQUATION SOLUTIONS WITH EXPLANATION AND TRICKS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
(p + 3) + 8 = 10
Question: What value of p is the solution to the given equation?
A) −1
B) 5
C) 15
D) 21
Choice A is correct. Subtracting 8 from both sides of the given equation yields p + 3 = 2. Subtracting 3 from both sides of this equation yields p = -1.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the equation
The equation is: (p + 3) + 8 = 10
Here, p is the variable we need to solve for.
Step 2: Simplify the equation
Combine the constants on the left-hand side:
p + 3 + 8 = 10
p + 11 = 10
Step 3: Isolate p
To solve for p, subtract 11 from both sides of the equation:
p = 10 − 11
p = −1
Step 4: Verify the solution
Substitute p = −1 back into the original equation to confirm:
((−1) + 3) + 8 = 10
2 + 8 = 10
This is true, so p = −1 is the correct solution.
Final Answer
The solution is: p = −1
2nd Question
Question:
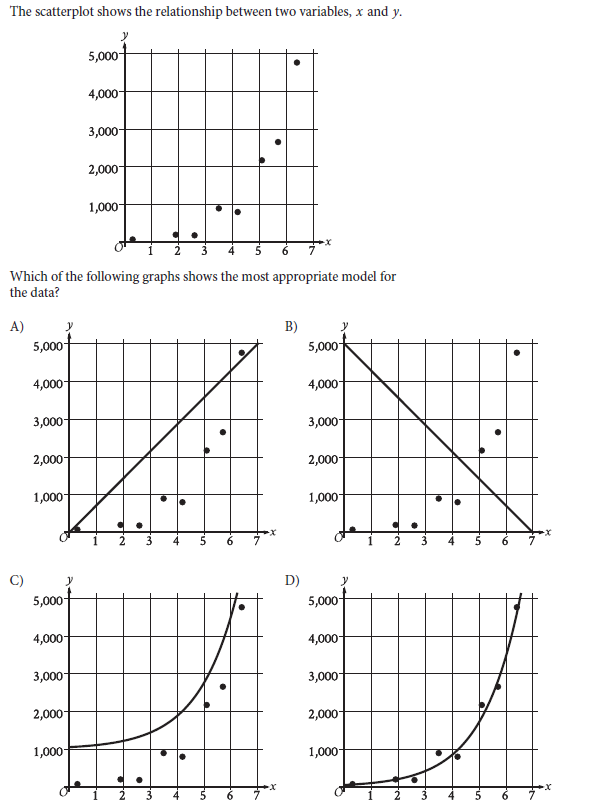
Choice D is correct. An appropriate model should follow the trend of the data points and should have data points both above and below the model. The scatterplot shows that the data points have an increasing trend that is curved. Therefore, an appropriate model should be an increasing curve with data points both above and below the model. Of the given choices, only the model in choice D is an increasing curve with data points both above and below the model.
Choice A is incorrect. Since the trend of the data points isn’t linear, a line isn’t the most appropriate model for the data.
Choice B is incorrect. Since the trend of the data points is increasing and isn’t linear, a decreasing line isn’t the most appropriate model for the data.
Choice C is incorrect. All the data points are below the model shown in this graph.
It is quite simple, as I suggest all the time, in Module 1st, you won’t get difficult questions. Hence, look carefully, you just need to follow the black data point; whatever the line matches the alignment of the dots that is the correct option. Option D is the one that follows the black data points.
3rd Question
k2 − 53 = 91
Question: What is the positive solution to the given equation?
A) 144
B) 72
C) 38
D) 12
Choice D is correct. Adding 53 to each side of the given equation yields k2 = 144. Taking the square root of each side of this equation yields k = +12. Therefore, the positive solution to the given equation is 12.
Choice A is incorrect. This is the positive solution to the equation k2 – 53 = 20683, not k2 – 53 = 91.
Choice B is incorrect. This is the positive solution to the equation k2 – 53 = 5131, not k2 – 53 = 91.
Choice C is incorrect. This is the positive solution to the equation k2 – 53 = 1391, not k2 – 53 = 91.
Step-by-Step Solution
You have two ways to do Step 1: First
k2 – 53 = 91 (-53 will move to the right-hand side and it will change its negative sign to positive.)
k2 = 91 + 53
k2 = 144
OR
Second
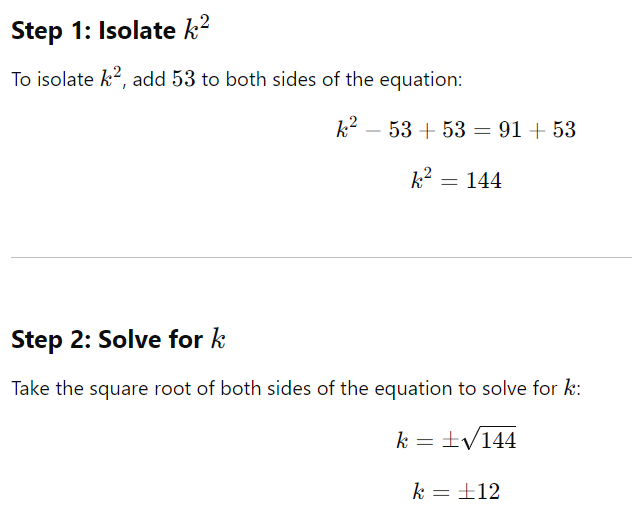
(Note: k2 = 144. Whenever you have a problem like this and you want to solve it, an exponential’s opposite is the root. Just like multiplying and dividing when you want to add 12 x 12 = 144 and 144/12 = 12.
We need the value of k, not k2. To get k, we know a square exponential opposite is a square root. Hence, the square of k transfers into a square root on the right-hand side for the solution.)
Step 3: Choose the Positive Solution
The question asks for a positive solution, so:
k =+12 (This + sign means, it can be positive or negative, your choice.)
k = 12.
4th Question
Question: During a portion of a flight, a small airplane’s cruising speed varied between 150 miles per hour and 170 miles per hour. Which inequality best represents this situation, where s is the cruising speed, in miles per hour, during this portion of the flight?
A) s ≤ 20
B) s ≤ 150
C) s ≤ 170
D) 150 ≤ s ≤ 170
Choice D is correct. It’s given that during a portion of a flight, a small airplane’s cruising speed varies between 150 miles per hour and 170 miles per hour. It’s also given that s represents the cruising speed, in miles per hour, during this portion of the flight. It follows that the airplane’s cruising speed, in miles per hour, was at least 150, which means s >150, and was at most 170, which means s < 170. Therefore, the inequality that best represents this situation is 150 < s < 170.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Since it is 4th question, it is not that difficult. The question might become complex based on given options. Option A and Option B are incorrect, but Option C is incomplete. When in question, you see something like ‘between’ always guess an option like D.
5th Question
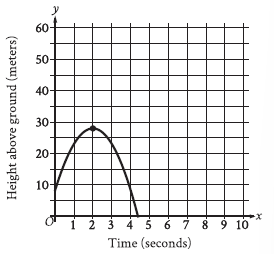
Question: An object was launched upward from a platform. The graph shown models the height above ground, y, in meters, of the object x seconds after it was launched. For which of the following intervals of time was the height of the object increasing for the entire interval?
A) From x = 0 to x = 2
B) From x = 0 to x = 4
C) From x = 2 to x = 3
D) From x = 3 to x = 4
Choice A is correct. It’s given that the variable y represents the height, in meters, of the object above the ground. The graph shows that the height of the object was increasing from x = 0 to x = 2, and decreasing from x = 2 to x = 4. Therefore, the height of the object was increasing for the entire interval of time from x = 0 to x = 2.
Choice B is incorrect. The height of the object wasn’t increasing for this entire interval of time, as it was decreasing from x = 2 to x = 4.
Choice C is incorrect. The height of the object was decreasing, not increasing, for this entire interval of time.
Choice D is incorrect. The height of the object was decreasing, not increasing, for this entire interval of time.
You should learn, how to understand a graph or so. Here, to understand the question and the time-consumption reading it is the major problem.
It asked, for maximum height. Based on the options and the question, we only need to focus on x.
The maximum height is the dot.
Step 1: Understand the graph
~ The graph represents the height y of an object above the ground over time x (in seconds).
~ Initially, the object is launched from a platform (height is non-zero at x = 0).
~ The object rises to a maximum height and then falls back down.
Step 2: Identify when the object’s height is increasing
The height of the object increases as long as the curve of the graph is sloping upward. This corresponds to the portion of the graph from x = 0 to the peak of the curve, which occurs at x = 2.
~ At x = 0: The object is launched upward from the platform.
~ At x = 2: The object reaches its maximum height.
~ Between x = 0 and x = 2, the height is continuously increasing because the graph shows a rising trend.
Step 3: Understand what happens after x = 2
~ At x = 2, the object reaches its highest point (the vertex of the parabola).
~ After x = 2, the height begins to decrease, as the curve slopes downward.
~ Therefore, the height of the object is not increasing after x = 2.
Step 4: Evaluate the options
Now, let’s analyze each option:
~ A) From x = 0 to x = 2:
This is correct because the graph shows the height increasing during this interval.
B) From x = 0 to x = 4:
Incorrect. While the height increases from x = 0 to x = 2, it decreases from x = 2 to x = 4.
C) From x = 2 to x = 3:
Incorrect. The graph slopes downward during this interval, so the height is decreasing, not increasing.
D) From x = 3 to x = 4:
Incorrect. The height is also decreasing during this interval.
Step 5: Conclusion
The height of the object is increasing only from x = 0 to x = 2, making A) From x = 0 to x = 2 the correct answer.
6th Question
Question: A teacher is creating an assignment worth 70 points. The assignment will consist of questions worth 1 point and questions worth 3 points. Which equation represents this situation, where x represents the number of 1-point questions and y represents the number of 3-point questions?
A) 4xy = 70
B) 4(x + y) = 70
C) 3x + y = 70
D) x + 3y = 70
Choice D is correct. Since x represents the number of 1-point questions and y represents the number of 3-point questions, the assignment is worth a total of 1 . x + 3 . y, or x + 3y, points. Since the assignment is worth 70 points, the equation x + 3y = 70 represents this situation.
Choice A is incorrect because we do not add values here.
Choice B is incorrect because we do not subtract values here.
Choice C is incorrect because we do not multiply values here.
Step 1: Analyze the problem requirements
~ The assignment is worth 70 points in total.
~ There are:
~ ~ x, the number of 1-point questions, contributing 1 ⋅ x points.
~ ~ y, the number of 3-point questions, contributing 3 ⋅ y points.
We are tasked with writing the equation that balances the total points from these two types of questions to equal 70 points.
Step 2: Examine each option
We will break down each equation and see if it matches the problem’s requirements:
Option A: 4xy = 70
~ This equation implies that the product of x, y, and 4 equals 70:
4 ⋅ x ⋅ y = 70
~ This is incorrect because the problem does not involve the product of x and y. Points are added together based on the number of 1-point and 3-point questions, not multiplied.
Option B: 4(x + y) = 70
~ This equation implies that the sum of x and y, multiplied by 4, equals 70:
4 ⋅ (x + y) = 70
~ This is incorrect because multiplying the sum of the number of questions by 4 does not represent the assignment’s point system. Each x contributes only 1 point, and each y contributes 3 points.
Option C: 3x + y = 70
~ This equation implies that each x contributes 3 points, and each y contributes 1 point:
3x + y = 70
~ This is incorrect because the problem states that x represents 1-point questions, and y represents 3-point questions. This equation swaps the roles of x and y.
Option D: x + 3y = 70
~ This equation implies that each x contributes 1 point, and each y contributes 3 points, and the total is 70:
x + 3y = 70
OR 1x + 3y = 70 (When you multiply 1 by x then you get x, so we can write either.)
~ This is correct because it matches the problem’s description:
~ ~ x, the number of 1-point questions, contributes 1 ⋅ x points.
~ ~ y, the number of 3-point questions, contributes 3 ⋅ y points.
~ Together, their total equals 70.
Step 3: Verify the correctness of Option D
To ensure x + 3y = 70 works, let’s test some sample values:
~ If x = 40 (40 one-point questions), then:
40 + 3y = 70
3y = 70 – 40
3y = 30
y = 30/3
y = 10
This satisfies the equation.
~ If x = 10 (10 one-point questions), then:
10 + 3y = 70
3y = 70 – 10
3y = 60
3y = 60/3
y = 20
This satisfies the equation as well.
Thus, Option D is correct.
7th Question
Question: Right triangles LMN and PQR are similar, where L and M correspond to P and Q, respectively. Angle M has a measure of 53°. What is the measure of angle Q?
A) 37°
B) 53°
C) 127°
D) 143°
Choice B is correct. It’s given that triangle LMN is similar to triangle PQR. Corresponding angles of similar triangles are congruent. Since angle M and angle Q correspond to each other, they must be congruent. Therefore, if the measure of angle M is 53o, then the measure of angle Q is also 53o.
Choice A is incorrect and may result from concluding that angle M and angle Q are complementary rather than congruent.
Choice C is incorrect and may result from the conclusion that angle M and angle Q are supplementary rather than congruent.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the problem
We are dealing with two similar right triangles (LMN and PQR), and we are tasked to determine the measure of angle Q given:
~ △LMN is similar to △PQR.
~ Angle L corresponds to angle P, and angle M corresponds to angle Q.
~ Angle M measures 53∘.
Step 2: Properties of similar triangles
In similar triangles:
1. Corresponding angles are equal.
~ Since M corresponds to Q, their measures will be the same.
~ Measure of ∠M = Measure of ∠Q.
2. The sum of the angles in any triangle is always 180∘. In a right triangle, one angle is 90∘, so the other two angles must sum to:
180∘ − 90∘ = 90∘.
Thus, the two non-right angles in a right triangle are complementary, meaning their measures add up to 90∘.
Step 3: Identify angle Q
From the given information:
~ Since ∠M measures 53∘, and ∠M corresponds to ∠Q, the measure of ∠Q is:
Measure of ∠Q = Measure of ∠M = 53∘.
Step 4: Verify the solution
Let’s double-check the relationship:
~ In △LMN, the angles are 90∘ (right angle), 53∘ (given), and the third angle:
90∘ − 53∘ = 37∘.
~ Since △LMN ∼ △PQR, the angles in △PQR will also be 90∘, 53∘, and 37∘.
Thus, ∠Q = 53∘ as it corresponds to ∠M.
Final Answer
The measure of ∠Q is: 53∘.
8th Question
y = -3x
4x + y = 15
Question: The solution to the given system of equations is (x, y). What is the value of x ?
A) 1
B) 5
C) 15
D) 45
Choice C is correct. The given system of linear equations can be solved by the substitution method. Substituting -3x for y from the first equation in the given system into the second equation yields 4x + (-3x) = 15, or x =15.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the absolute value of y, not the value of x .
Step-by-Step Solution
Step 1: Substitute y from the first equation into the second equation
From the first equation, y = −3x. Substitute y into the second equation 4x + y = 15:
4x + (−3x) = 15
Simplify:
4x − 3x = 15
x = 15
Step 2: Verify the solution
To verify, substitute x = 15 back into both equations.
1. From y = −3x:
y = −3(15) = −45
2. Substitute x = 15 and y = −45y into 4x + y = 15:
4(15) + (−45) = 15
60 − 45 = 15
This is true, so x = 15 is correct.
9th Question
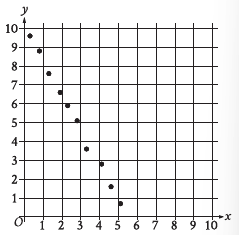
Question: Which of the following equations is the most appropriate linear model for the data shown in the scatterplot?
A) y = -1.9x – 10.1
B) y = -1.9x + 10.1
C) y = 1.9x – 10.1
D) y = 1.9x + 10.1
Choice B is correct. The equation representing a linear model can be written in the form y = a + bx, or y = bx + a, where b is the slope of the graph of the model and (0, a) is the y-intercept of the graph of the model. The scatterplot shows that as the x-values of the data points increase, the y-values of the data points decrease, which means the graph of an appropriate linear model has a negative slope. Therefore, b < 0. The scatterplot also shows that the data points are close to the y-axis at a positive value of y. Therefore, the y-intercept of the graph of an appropriate linear model has a positive y-coordinate, which means a > 0. Of the given choices, only choice B, y = -1.9x + 10.1, has a negative value for b, the slope, and a positive value for a, the y-coordinate of the y-intercept.
Choice A is incorrect. The graph of this model has a y-intercept with a negative y-coordinate, not a positive y-coordinate.
Choice C is incorrect. The graph of this model has a positive slope, not a negative slope, and a y-intercept with a negative y-coordinate, not a positive y-coordinate.
Choice D is incorrect. The graph of this the model has a positive slope, not a negative slope.
Sometimes, you will see questions like these, where there are many answers based on what value you choose from the graph. I suggest in situations like these, you should focus on options and decide what to do.
Here, the values are the same except for the positive or negative sign. So it doesn’t matter what value you choose or what answer you get; focus on the signs only.
Step 1: Observe the trend in the scatterplot
~ The scatterplot shows a negative linear relationship between x and y.
~ As x increases, y decreases steadily, indicating a negative slope.
~ This suggests a linear equation of the form y = mx + b, where m is negative.

Step 4: Determine the y-intercept b:
~ Using the point (1, 10) and the slope m = −1.5:
y = mx + b
10 = (−1.5)(1) + b
10 = −1.5 + b
b = 10 + 1.5
b = 11.5.
Step 5: Construct the equation:
The equation of the line is: y = −1.5x + 11.5
Step 6: Verify the fit:
~ Substituting x = 3:
y = −1.5(3) + 11.5
y = −4.5 + 11.5
y = 7, which matches the scatterplot.
~ Substituting x = 5:
y = −1.5(5) + 11.5
y = −7.5 + 11.5
y = 4, which matches the scatterplot.
This confirms the equation fits the data well.
10th Question
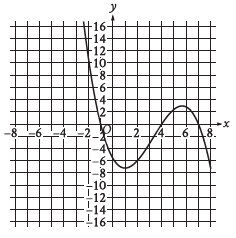
Question: The graph of y = f(x) is shown, where the function f is defined by f(x) = ax3 + bx2 + cx + d and a, b, c, and d are constants. For how many values of x does f(x) = 0 ?
A) One
B) Two
C) Three
D) Four
Choice C is correct. If a value of x satisfies f(x) = 0, the graph of y = f(x) will contain a point (x, 0) and thus touch the x-axis. Since there are 3 points at which this graph touches the x-axis, there are 3 values of x for which f(x) = 0.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem:
The question asks for the number of values of xxx where f(x) = 0. This means we need to find the x-intercepts of the given graph. The function f(x) is a cubic polynomial, so it can have up to three real roots (solutions).
Step-by-Step Explanation:
1. Interpret the graph:
The graph of y = f(x) intersects the x-axis wherever f(x) = 0. These are the x-intercepts of the graph.
2. Locate the x-intercepts:
~ From the graph, we observe that the curve crosses the x-axis at three distinct points:
~ ~ The first x-intercept is around x = 0.
~ ~ The second x-intercept is around x = 4.
~ ~ The third x-intercept is around x = 7.
3. Confirm the number of solutions:
~ The graph crosses the x-axis at exactly three points, meaning there are three values of x for which f(x) = 0.
4. Relate to the degree of the polynomial:
~ The given function f(x) = ax3 + bx2 + cx + d is a cubic polynomial (a ≠ 0). A cubic polynomial can have:
~ ~ Up to three real roots.
~ ~ A minimum of one real root (since a cubic polynomial always has at least one real solution).
~ ~ Since the graph has three x-intercepts, all three roots are real and distinct.
Conclusion:
The function f(x) = 0 has three solutions, corresponding to the three x-intercepts observed in the graph.
What is a Cubic polynomial here?
The equation f(x) = ax3 + bx2 + cx + d is explicitly given in the problem statement, and the term ax3 confirms that this is a cubic polynomial. The degree of a polynomial is determined by the highest power of x, which in this case is 3.
Additionally, the shape of the graph provides further confirmation. Key characteristics of cubic polynomial graphs include:
1. Three turning points or inflection points: The graph exhibits the characteristic “S” shape of cubic polynomials, with peaks and valleys.
2. Behavior at the ends: For cubic polynomials, one end of the graph approaches +∞ while the other end approaches −∞, as seen in the provided graph. (Notice: The graph doesn’t show the end point and it has an infinite negative-axis and infinitive positive-axis.)
Thus, both the explicit equation and the graph confirm that this is a cubic polynomial.
11th Question
Question: The function f(w) = 6w2 gives the area of a rectangle, in square feet (ft2), if its width is w ft and its length is 6 times its width. Which of the following is the best interpretation of f(14) = 1,176 ?
A) If the width of the rectangle is 14 ft, then the area of the rectangle is 1,176 ft2.
B) If the width of the rectangle is 14 ft, then the length of the rectangle is 1,176 ft.
C) If the width of the rectangle is 1,176 ft, then the length of the rectangle is 14 ft.
D) If the width of the rectangle is 1,176 ft, then the area of the rectangle is 14 ft2.
Choice A is correct. The function f gives the area of the rectangle, in ft2, if its width is w ft. Since the value of f(14) is the value of f(w) if w =14, it follows that f(14) = 1,176 means that f(w) is 1,176 if w = 14. In the given context, this means that if the width of the rectangle is 14 ft, then the area of the rectangle is 1,176 ft2.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors
Choice D is incorrect and may result from interpreting f(w) as the width, in ft, of the rectangle if its area is w ft2, rather than as the area, in ft2, of the rectangle if its width is w ft.
Problem Breakdown
We are tasked with interpreting the equation f(w) = 6w2, where f(w) represents the area of a rectangle given its width w and its length is 6 times the width.
We are specifically asked to interpret f(14) = 1,176.
Step-by-Step Solution
Step 1: Understand the function f(w) = 6w2
~ In this function:
~ ~ w is the width of the rectangle in feet.
~ ~ The length of the rectangle is 6 × w.
~ ~ The area of the rectangle, in square feet, is the product of the length and the width:
Area = Length × Width
(6w) × w = 6w2
Thus, f(w) directly gives the area of the rectangle for a given width w.
Step 2: Substitute w = 14 into the function
We are given f(14) = 1,176. Let’s verify this:
f(w) = 6w2
f(14) = 6 × 142
f(14) = 6 ×196
f(14) = 1,176
This confirms that if the width of the rectangle is 14 feet, then the area of the rectangle is 1,176 square feet.
Step 3: Interpret f(14) = 1,176
~ The input w = 14 represents the width of the rectangle.
~ The output f(14) = 1,176 represents the area of the rectangle.
~ Thus, the correct interpretation is: If the width of the rectangle is 14 ft, then the area of the rectangle is 1,176 ft2.
This matches Option A.
Step 4: Evaluate Other Options
~ Option B: Incorrect, because 1,176 represents the area, not the length.
~ Option C: Incorrect, because w = 1,176 makes no sense for the width, given the large value.
~ Option D: Incorrect, because 14 does not represent the area; it represents the width.
Final Answer: Option A
12th Question
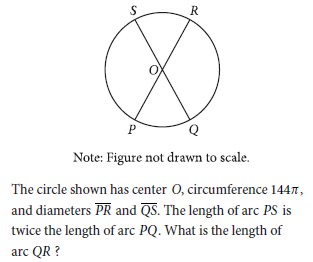
Question:
A) 24π
B) 48π
C) 72π
D) 96π
Choice B:

Since it’s given that the circumference is 144π, the expression x + x + 2x + 2x is equal to 144π . Thus x + x + 2x + 2x = 144π , or 6x = 144π . Dividing both sides of this equation by 6 yields x = 24π . Therefore, the length of arc QR is 2(24π), or 48π.
Choice A is incorrect. This is the length of arc PQ, not arc QR
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the given information
1. The circle has:
~ Center O.
~ Circumference 144π.
2. The lengths of arcs:
~ Arc PS is twice the length of arc PQ.
~ Arc PS = 2 × Arc PQ.
3. We are tasked to find the length of the arc QR.

Step 4: Analyze arc distribution
~ Diameters PR and QS divide the circle into 4 arcs: PQ, PS, QR, and SR.
~ Opposite arcs must also be equal:
~ ~ Arc PQ = Arc SR
~ ~ Arc PS = Arc QR.
Thus:
Arc SR = x, Arc QR = 2x.
Step 5: Set up the equation
The sum of all arc lengths is equal to the circumference:
x + 2x + 2x + x = 144π.
Simplify:
6x = 144π.
Step 6: Solve for x
x = 144π/6 = 24π.
Thus:
~ Arc PQ = x = 24π,
~ Arc PS = 2x = 48π,
~ Arc QR = 2x = 48π,
~ Arc SR = x = 24π.
Step 7: Final answer
The length of arc QR is: 48π.
13th Question
Question: A company that provides whale-watching tours takes groups of 21 people at a time. The company’s revenue is 80 dollars per adult and 60 dollars per child. If the company’s revenue for one group consisting of adults and children was 1,440 dollars, how many people in the group were children?
A) 3
B) 9
C) 12
D) 18
Choice C is correct. Let x represent the number of children in a whale-watching tour group. Let y represent the number of adults in this group. Because it’s given that 21 people are in a group and the group consists of adults and children, it must be true that x + y = 21. Since the company’s revenue is 60 dollars per child, the total revenue from x children in this group was 60x dollars. Since the company’s revenue is 80 dollars per adult, the total revenue from y adults in this group was 80y dollars. Because it’s given that the total revenue for this group was 1,440 dollars, it must be true that 60x + 80y = 1,440. The equations x + y = 21 and 60x + 80y = 1,440 form a linear system of equations that can be solved to find the value of x, which represents the number of children in the group, using the elimination method. Multiplying both sides of the equation x + y = 21 by 80 yields 80x + 80y = 1,680. Subtracting 60x + 80y = 1,440 from 80x + 80y = 1,680 yields (80x + 80y) – (60x + 80y) = 1,680 – 1,440, which is equivalent to 80x – 60x + 80y – 80y = 240, or 20x = 240. Dividing both sides of this equation by 20 yields x = 12. Therefore, 12 people in the group were children.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect. This is the number of adults in the group, not the number of children in the group.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Define the Variables
Let:
~ a = number of adults in the group
~ c = number of children in the group
The total number of people in the group is 21:
a + c = 21
The company’s total revenue from this group is $1,440, with $80 per adult and $60 per child:
80a + 60c = 1440
Step 2: Solve the System of Equations
We now have two equations:
~ a + c = 21
~ 80a + 60c = 1440
Step 2.1: Simplify Equation (2)
Divide the entire second equation by 20 to simplify:
4a + 3c = 72
Step 2.2: Solve for a in Terms of c
From Equation (1): a = 21 − c
Step 2.3: Substitute a = 21 − c into Equation (3)
Substitute a = 21 − c into 4a + 3c = 72:
4(21 − c) + 3c = 72
Expand and simplify: 84 − 4c + 3c = 72
Combine like terms: 84 − c = 72
Solve for c: c = 84 − 72
c = 12
Step 3: Solve for a
Substitute c = 12 into Equation (1):
a + 12 = 21
Solve for a:
a = 21 − 12
a = 9
Step 4: Verify the Solution
~ Total number of people: a + c = 9 + 12
a = 21 ✔️
~ Total revenue: 80a + 60c
80(9) + 60(12)
720 + 720 = 1440 ✔️
The solution is consistent with the problem’s conditions.
Final Answer
The number of children in the group is: 12.
14th Question
Question: The relationship between two variables, x and y, is linear. For every increase in the value of x by 1, the value of y increases by 8. When the value of x is 2, the value of y is 18. Which equation represents this relationship?
A) y = 2x + 18
B) y = 2x + 8
C) y = 8x + 2
D) y = 3x + 26
Choice C is correct. It’s given that the relationship between x and y is linear. An equation representing a linear relationship can be written in the form y = mx + b, where m is the slope and b is the y-coordinate of the y-intercept of the graph of the relationship in the xy-plane. It’s given that for every increase in the value of x by 1, the value of y increases by 8. The slope of a line can be expressed as the
change in y over the change in x. Thus, the slope, m, of the line representing this relationship can be expressed as 18, or 8. Substituting 8 for m in the equation y = mx + b yields y = 8x + b. It’s also given that when the value of x is 2, the value of y is 18. Substituting 2 for x and 18 for y in the equation y = 8x + b yields 18 = 8(2) + b, or 18 = 16 + b. Subtracting 16 from each side of this equation yields 2 = b. Substituting 2 for b in the equation y = 8x + b yields y = 8x + 2. Therefore, the equation y = 8x + 2 represents this relationship.
Choice A is incorrect. This equation represents a relationship where for every increase in the value of x by 1, the value of y increases by 2, not 8, and when the value of x is 2, the value of y is 22, not 18.
Choice B is incorrect. This equation represents a relationship where for every increase in the value of x by 1, the value of y increases by 2, not 8, and when the value of x is 2, the value of y is 12, not 18.
Choice D is incorrect. This equation represents a relationship where for every increase in the value of x by 1, the value of y increases by 3, not 8, and when the value of x is 2, the value of y is 32, not 18.
Step-by-Step Solution
The problem states that the relationship between x and y is linear. This means the equation will have the form:
y = mx + b
where:
~ m is the slope of the line (rate of change of y with respect to x), and
~ b is the y-intercept (value of y when x = 0).
Step 1: Identify the slope (m)
We are told that for every increase in x by 1, y increases by 8. This means the slope is:
m = 8
Thus, the equation becomes:
y = 8x + b
Step 2: Find the y-intercept (b)
We are given that when x = 2, y = 18. Substituting these values into the equation y = 8x + b:
18 = 8(2) + b
Simplify: 18 = 16 + b
Solve for b: b = 18 − 16
b = 2
Step 3: Write the final equation
Substitute m = 8 and b = 2 into the equation y = mx + b:
y = 8x + 2
Step 4: Verify
To ensure the equation is correct, substitute the known point (x = 2, y = 18) into y = 8x + 2:
y = 8(2) + 2
y = 16 + 2
y = 18
The equation is correct.
Final Answer
The equation that represents this relationship is: y = 8x + 2
15th Question
Question:
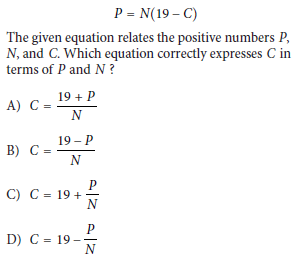
Choice D
Choice A is incorrect. This equation is equivalent to P = NC – 19, not P = N(19 – C).
Choice B is incorrect. This equation is equivalent to P = 19 – NC, not P = N(19 – C).
Choice C is incorrect. This equation is equivalent to P = N(C – 19), not P = N(19 – C).
Step-by-Step Solution
We are tasked with solving the given equation P = N(19 − C) for C, expressing it in terms of P and N. Let’s work through this step by step.
Step 1: Write the original equation
The equation is:
P = N(19 − C)
Our goal is to isolate C.
Step 2: Divide both sides by N
Since N ≠ 0 (it’s given that N is positive), divide both sides of the equation by N to eliminate the multiplication on the right-hand side:


This confirms the solution is correct.
16th Question
Question:
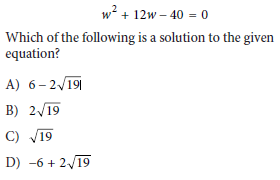
Choice D
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
We are solving the quadratic equation:
w2 + 12w − 40 = 0
and determining which of the provided options is a solution.
Step 1: Identify the coefficients
The quadratic equation is written in the standard form ax2 + bx + c = 0, where:
a = 1, b = 12, c = −40


17th Question
Question: A circle in the xy-plane has a diameter with endpoints (2, 4) and (2,14). An equation of this circle is (x − 2)2 + (y − 9)2 = r2, where r is a positive constant. What is the value of r ?
A) 10
B) 7
C) 5
D) 13
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice C:

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
We are tasked with finding the value of r, the radius of a circle, given that the equation of the circle is:
(x − 2)2 + (y − 9)2 = r2
The endpoints (2, 4) and (2, 14) define the circle’s diameter.
Step 1: Determine the center of the circle
The center of the circle is the midpoint of the diameter. The formula for the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is:

Step 3: Verify the equation
The circle’s equation is given as:
(x − 2)2 + (y − 9)2 = r2
Substitute r = 5:
(x − 2)2 + (y − 9)2 = 52
Hence: r2 = 52 = 25
The value of r is confirmed to be: 5
18th Question
Question:
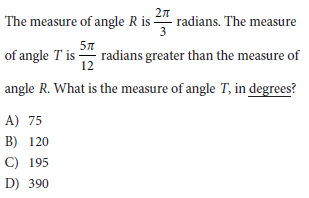
Choice C
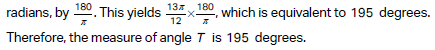
Choice A is incorrect. This is the number of degrees that the measure of angle T is greater than the measure of angle R.
Choice B is incorrect. This is the measure of angle R, in degrees.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:


Final Answer
The measure of angle T is: 195 degrees.
19th Question
Question: The function g is defined by g(x) = (x + 14)(t − x), where t is a constant. In the xy-plane, the graph of y = g(x) passes through the point (24, 0). What is the value of g(0)?
A) 336
B) 24
C) 14
D) 338
Choice A: The correct answer is 336. By the zero product property, if (x + 14)(t – x) = 0, then x + 14 = 0, which gives x =-14, or (t – x) = 0, which gives x = t. Therefore, g(x) = 0 when x = -14 and when x = t. Since the graph of y = g(x) passes through the point (24, 0), it follows that g(24) = 0, so t = 24. Substituting 24 for t in the equation g(x) = (x + 14)(t – x) yields g(x) = (x + 14)(24 – x). The value of
g(0) can be calculated by substituting 0 for x in this equation, which yields g(0) = (0 + 14)(24 – 0), or g(0) = 336.
Choice A is incorrect. This is the value of a, not x.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
We are tasked with finding the value of g(0), where the function g(x) = (x + 14)(t − x) and the graph passes through the point (24, 0).
Step 1: Use the given point to find the value of t
The function passes through (24, 0), meaning that g(24) = 0. Substitute x = 24 and g(24) = 0 into the function:
g(24) = (24 + 14)(t − 24)
0 = (38)(t − 24)
Since 38 ≠ 0, we know:
t − 24 = 0
t = 24
Step 2: Substitute t = 24 into g(x)
Now that we know t = 24, the function becomes:
g(x) = (x + 14)(24 − x)
Step 3: Find g(0)
To find g(0), substitute x = 0 into g(x):
g(0) = (0 + 14)(24 − 0)
g(0) = 14 ⋅ 24
g(0) = 336
Final Answer
The value of g(0) is: 336
20th Question
(x + 4)2 + (y − 19)2 = 121
Question: The graph of the given equation is a circle in the xy-plane. The point (a, b) lies on the circle. Which of the following is a possible value for a ?
A) −16
B) −14
C) 11
D) 19
Choice B is correct. An equation of the form (x – h)2 + (y – k)2 = r2, where h, k, and r are constants, represents a circle in the xy-plane with center (h, k) and radius r. Therefore, the circle represented by the given equation has center (-4, 19) and radius 11. Since the center of the circle has an x-coordinate of -4 and the radius of the circle is 11, the least possible x-coordinate for any point on the circle is -4 -11, or -15. Similarly, the greatest possible x-coordinate for any point on the circle is -4 + 11, or 7. Therefore, if the point (a, b) lies on the circle, it must be true that -15 < a < 7. Of the given choices, only -14 satisfies this inequality.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
The equation of the circle is:
(x + 4)2 + (y − 19)2 = 121
We are asked to determine a possible value for a, the x-coordinate of a point (a, b) lying on the circle.
Step 1: Equation of a circle in standard form
The equation of the circle is in the standard form:
(x − h)2 + (y − k)2 = r2
Here:
~ The center of the circle is (−4, 19).
~ The radius of the circle is:
r2 = 121 (square exponential of r moves to the right-side and transforms into a square root.)
r = square root of 121
r =11.
This means that any point (x, y) on the circle is exactly 11 units away from the center (−4, 19).
Step 2: Understanding the problem
We need to determine a possible value of a, the x-coordinate of a point (a, b) that lies on the circle. To do so, we will:
~ Substitute x = a into the equation of the circle.
~ Solve for y (the y-coordinate, or b, of the point).
~ Ensure the resulting equation satisfies the conditions of the circle.
Step 3: Plug x = a into the circle equation
Substitute x = a into the equation:
(a + 4)2 + (y − 19)2 = 121
Rearrange to solve for (y − 19)2:
(y − 19)2 = 121 − (a + 4)2

It is already clear that out of all the options which option is between -15 and 7 but still let’s understand it thoroughly.
Step 5: Verify the options
We now check each option to determine which satisfies the equation of the circle.

Step 6: Conclusion
The only valid solution is: −14
21th Question
Question: A right rectangular prism has a height of 9 inches. The length of the prism’s base is x inches, which is 7 inches more than the width of the prism’s base. Which function V gives the volume of the prism, in cubic inches, in terms of the length of the prism’s base?
A) V(x) = x(x + 9)(x + 7)
B) V(x) = x(x + 9)(x − 7)
C) V(x) = 9x(x + 7)
D) V(x) = 9x(x − 7)
Choice D is correct. The volume of a right rectangular prism can be represented by a function V that gives the volume of the prism, in cubic inches, in terms of the length of the prism’s base. The volume of a right rectangular prism is equal to the area of its base times its height. It’s given that the length of the prism’s base is x inches, which is 7 inches more than the width of the prism’s base. This means
that the width of the prism’s base is x – 7 inches. It follows that the area of the prism’s base, in square inches, is x(x – 7), and the volume, in cubic inches, of the prism is x(x – 7)(9). Thus, the function V that gives the volume of this right rectangular prism, in cubic inches, in terms of the length of the prism’s base, x, is V(x) = 9x(x – 7).
Choice A is incorrect. This function would give the volume of the prism if the height were 9 inches more than the length of its base and the width of the base were 7 inches more than its length.
Choice B is incorrect. This function would give the volume of the prism if the height were 9 inches more than the length of its base.
Choice C is incorrect. This function would give the volume of the prism if the width of the base were 7 inches more than its length, rather than the length of the base being 7 inches more than its width.
We are tasked with finding a function for the volume V of a right rectangular prism in terms of the length of its base, x. Let’s solve this step by step.
Step 1: Recall the formula for the volume of a rectangular prism
The formula for the volume V of a rectangular prism is:
V = length × width × height.
From the problem, we are given:
~ The length of the prism’s base is x inches.
~ The width of the prism’s base is x − 7 inches (as it is 7 inches less than the length).
~ The height of the prism is 9 inches.
Step 2: Write the volume function in terms of x
Substitute the given dimensions into the volume formula:
V = (length) × (width) × (height).
Substituting the known values: V = x × (x − 7) × 9. (x multiply by (x – 7) multiply by 9)
Step 3: Simplify the expression for V
Distribute x and (x − 7):
V = 9 ⋅ x ⋅ (x − 7).
V = 9x(x – 7). We have already got Option D here. We can solve it more but the options are here to save our time. But for practice purposes, you should solve the whole problem.
V = 9x(x – 7).
V = 9x2 – 63x
22th Question
Question: The function f is defined by f(x) = ax2 + bx + c, where a, b, and c are constants. The graph of y = f(x) in the xy-plane passes through the points (7, 0) and (−3, 0). If a is an integer greater than 1, which of the following could be the value of a + b?
A) −6
B) −3
C) 4
D) 5
Choice A is correct. It’s given that the graph of y = f(x) in the xy-plane passes through the points (7, 0) and (-3, 0). It follows that when the value of x is either 7 or -3, the value of f(x) is 0. It’s also given that the function f is defined by f(x) = ax2 + bx + c, where a, b, and c are constants. It follows that the function f is a quadratic function and, therefore, may be written in factored form as f(x) = a(x – u)(x – v), where the value of f(x) is 0 when x is either u or v. Since the value of f(x) is 0 when the value of x is either 7 or -3, and the value of f(x) is 0 when the value of x is either u or v, it follows that u and v are equal to 7 and -3. Substituting 7 for u and -3 for v in the equation f(x) = a(x – u)(x – v) yields f(x) = a(x – 7)(x – (-3)), or f(x) = a(x – 7)(x + 3). Distributing the right-hand side of this equation yields f(x) = a(x2 – 7x + 3x – 21), or f(x) = ax2 – 4ax – 21a. Since it’s given that f(x) = ax2 + bx + c, it follows that b = -4a. Adding a to each side of this equation yields a + b = -3a. Since a + b = -3a, if a is an integer, the value of a + b must be a multiple of 3. If a is an integer greater than 1, it follows that a > 2. Therefore, -3a < -3(2). It follows that the value of a + b is less than or equal to -3(2), or -6. Of the given choices, only -6 is a multiple of 3 that’s less than or equal to -6.
Choice B is incorrect. This is the value of a + b if a is equal to, not greater than, 1.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
To solve this problem step by step, we will determine the possible value of a + b given the function f(x) = ax2 + bx + c, with additional conditions about the roots and coefficients.
Step 1: General form of a quadratic equation
The function f(x) = ax2 + bx + c has roots x = 7 and x = −3. Using the factored form of a quadratic equation, we can write:
f(x) = a(x − 7)(x + 3),
where a is the leading coefficient.
Step 2: Expand the equation
Expand f(x) to standard quadratic form:
f(x) = a[(x − 7)(x + 3)].
First, expand (x − 7)(x + 3):
(x − 7)(x + 3)
x2 − 7x + 3x −21
x2− 4x − 21.
Substitute this back: f(x) = a(x2 − 4x − 21).
Distribute a: f(x) = ax2 − 4ax − 21a.
From this, we can identify:
~ The coefficient of x2 is a,
~ The coefficient of x is −4a,
~ The constant term is −21a.
Step 3: Relate b to a
From the expanded form f(x) = ax2 − 4ax − 21a, the coefficient b is:
b = −4a.
Step 4: Calculate a + b
Substitute b = −4a into a + b:
a + b = a − 4a = −3a.
Step 5: Determine possible values of a + b
Since a is an integer greater than 1 (a > 1), the smallest possible value of a is 2.
Substituting a = 2 into a + b:
a + b = −3a
a + b =−3(2)
a + b =−6.
If a = 3, then:
a + b = −3a
a + b = −3(3)
a + b = −9.
Thus, possible values for a + b are multiples of −3 (e.g., −6,−9,−12,-15, -18, etc.) but not -3.
Step 6: Select a valid option
Remember, we are looking for multiples of -3, not just -3. A multiple means numbers that come into the table of 3. So, Option A is the correct answer.
Did you try all the features and get comfortable using them? You should work on using the calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must try to work on your speed and spend less time on the beginning and more on the later questions. This is the 3rd Practice Test of SAT Math Module 1st.
Either you can take the 4th Practice Test of SAT Math or the 3rd Practice Test of SAT Math Module 2nd.
- SAT Test 3rd (Math Module 2nd)
- SAT Test 4th (Math Module 1st)
- SAT Test 3rd (Reading and Writing Module 1st)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


