
Solution of the SAT Math Test Question: Module 2nd with Tricks to get 1560 Marks
Have you taken the module 1st? If yes, then you are in the right place. This is the 3rd Test of Module 2nd. We have designed a similar exam format with all the necessary features for you to become a master in Math. You take the SAT Test Module Second to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 2nd.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 2ND
The second module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 2nd are only difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 2nd. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH STUDY GUIDE AND PROBLEM SOLUTIONS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
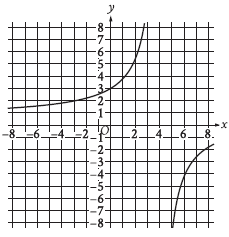
Question: The graph of y = f(x) is shown in the xy-plane. What is the value of f(0)?
A) −3
B) 0
C) 3/5
D) 3
Choice D is correct. Because the graph of y = f(x) is shown, the value of f(0) is the value of y on the graph that corresponds with x = 0. When x = 0, the corresponding value of y is 3. Therefore, the value of f(0) is 3.
Choice A is incorrect and may result from conceptual errors.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Step 1: Restate the question
The task is to find the value of f(0), which corresponds to the y-coordinate of the graph at the point where x = 0.
Step 2: Locate x = 0 on the graph
~ The x = 0 line is the y-axis.
~ Find where the curve intersects the y-axis.
Step 3: Read the y-coordinate at x = 0
From the graph:
~ At x = 0, the curve intersects the y-axis at y = 3.
Thus:
f(0) = 3.
Step 4: Verify the solution
Inspecting the graph carefully shows that the curve passes through (0, 3). This confirms that the value of f(0) is indeed 3.
Final Answer: f(0) = 3.
2nd Question
Question: Which expression is equivalent to (m4q4z-1)(mq5z3), where m, q, and z are positive?
A) m4q20z-3
B) m5q9z2
C) m6q8z-1
D) m20q12z-2
Choice B is correct. Applying the commutative property of multiplication, the expression (m4q4z-1)(mq5z3) can be rewritten as (m4m)(q4q5)(z-1z3). For positive values of x, (xa)(xb) = xa+b. Therefore, the expression (m4m)(q4q5)(z-1z3) can be rewritten as (m4+1)(q4+5)(z-1+3), or m5q9z2.
Choice A is incorrect and may result from multiplying, not adding, the exponents.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Write down the given expression
The expression is:
(m4q4z−1)(mq5z3)
Step 2: Simplify the exponents of m
~ In the first term, m4, and in the second term, m1 (since m = m1).
~ When multiplying terms with the same base, add the exponents:
m4 ⋅ m1
= m4 + 1
=m5
Step 3: Simplify the exponents of q
~ In the first term, q4, and in the second term, q5.
~ Again, add the exponents:
q4 ⋅ q5
= q4 + 5
= q9
Step 4: Simplify the exponents of z
~ In the first term, z-1, and in the second term, z3.
~ Add the exponents:
z-1 ⋅ z3
= z-1 + 3
= z2
Step 5: Combine the simplified terms
Now, combining all the results:
m5q9z2
Step 6: Compare with the answer choices
The simplified expression matches Choice B: m5q9z2
Final Answer: B) m5q9z2.
3rd Question
73, 74, 75, 77, 79, 82, 84, 85, 91
Question: What is the median of the data shown?
A) 78
B) 79
C) 80
D) 81
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 79. The median of a data set with an odd number of values is the middle value of the set when the values are ordered from least to greatest. Because the given data set consists of nine values that are ordered from least to greatest, the median is the fifth value in the data set. Therefore, the median of the data shown is 79.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand what the median represents
The median is the middle value in a dataset when the numbers are arranged in ascending order. If the dataset contains an odd number of values, the median is the middle value. If the dataset contains an even number of values, the median is the average of the two middle values.
Step 2: Write down the data
The given dataset is:
73, 74, 75, 77, 79, 82, 84, 85, 91
Step 3: Count the number of data points
There are 9 data points in the dataset:
73, 74, 75, 77, 79, 82, 84, 85, 91 (9 values)
Since there is an odd number of data points, the median is the value in the middle.
Step 4: Identify the middle value
To find the middle value:
Middle index = n + 1/2 (n + 1 is divided by 2)
where n = 9 (total number of data points).
Middle index = 9 + 1/2 =5
So, the 5th value in the dataset is the median.
Step 5: Locate the 5th value
The dataset in ascending order is: 73, 74, 75, 77, 79, 82, 84, 85, 91
The 5th value is 79.
Step 6: Verify the answer
The median is the middle value of an ordered dataset, and since the dataset has an odd number of values, there is no need to calculate an average. The correct answer is 79.
Final Answer: The median is: 79.
4th Question
x + 40 = 95
Question: What value of x is the solution to the given equation?
A) 55x
B) 55
C) 135x
D) 135
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 55. Subtracting 40 from both sides of the given equation yields x = 55. Therefore, the value of x is 55.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the equation
The given equation is:
x + 40 = 95
This is a simple linear equation where we need to isolate x by performing operations to eliminate the constant on the left side.
Step 2: Subtract 40 from both sides
To isolate x, subtract 40 from both sides of the equation:
x + 40 − 40 = 95 − 40
Simplify: x = 55
Step 3: Verify the solution
To ensure the solution is correct, substitute x = 55 back into the original equation:
55 + 40 = 95
This simplifies to: 95 = 95
Since both sides are equal, the solution is correct.
Final Answer: The value of x is: 55.
5th Question
5x = 15
-4x + y = -2
Question: The solution to the given system of equations is (x, y). What is the value of x + y?
A) −17
B) −13
C) 13
D) 17
Choice C is correct. Adding the second equation of the given system to the first equation yields 5x + (-4x + y) = 15 + (-2), which is equivalent to x + y = 13. So the value of x + y is 13.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect. This is the value of -(x + y).
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Solve for x from the first equation
The first equation is: 5x = 15
To isolate x, divide both sides of the equation by 5:
x = 15/5
x = 3
Step 2: Substitute x = 3 into the second equation
The second equation is:
−4x + y = −2
Substitute x = 3 into the equation:
−4(3) + y = −2
Simplify:
−12 + y = −2
Add 12 to both sides to isolate y:
y = −2 + 12
y = 10
Step 3: Calculate x + y
Now that we know x = 3 and y = 10, add them together:
x + y
= 3 + 10
= 13.
Verification
To verify the solution, substitute x = 3 and y = 10 back into both original equations:
1) 5x = 15:
5(3) = 15, which is true.
2) −4x + y = −2:
−4(3) + 10
= −12 + 10
= −2, which is true.
Both equations are satisfied, so the solution is correct.
Final Answer: C) 13.
6th Question
Question: The function f defined by f(t) = 14t + 9 gives the estimated length, in inches, of a vine plant t months after Tavon purchased it. Which of the following is the best interpretation of 9 in this context?
A) Tavon will keep the vine plant for 9 months.
B) The vine plant is expected to grow 9 inches each month.
C) The vine plant is expected to grow to a maximum length of 9 inches.
D) The estimated length of the vine plant was 9 inches when Tavon purchased it.
Choice D is correct. It’s given that the function f defined by f(t) = 14t + 9 gives the estimated length, in inches, of a vine plant t months after Tavon purchased it. For a function defined by an equation of the form f(t) = mt + b, where m and b are constants, b represents the value of f(0), or the value of f(t) when the value of t is 0. Therefore, for the function defined by f(t) = 14t + 9, 9 represents the value of f(t) when the value of t is 0. This means that 0 months after the vine plant was purchased, the estimated length of the vine plant was 9 inches. Therefore, the best interpretation of 9 in this context is the estimated length of the vine plant was 9 inches when Tavon purchased it.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect. The vine plant is expected to grow 14 inches, not 9 inches, each month.
Choice C is incorrect and may result from conceptual or calculation errors.
We are tasked with interpreting the constant 9 in the linear function:
f(t) = 14t + 9
where f(t) represents the estimated length (in inches) of a vine plant t months after Tavon purchased it.
Step 1: Understand the components of the equation
This equation is in the form of a linear function:
f(t) = mt + b
where:
~ m (14) represents the rate of change (the growth rate of the vine per month, in this case).
~ b (9) represents the initial value (the length of the vine when t = 0, or when the plant was first purchased).
Step 2: Substitute t = 0
To understand the role of b = 9, substitute t = 0 into the equation:
f(0) = 14(0) + 9
f(0) = 9
This shows that when Tavon purchased the vine plant (t = 0), the estimated length of the plant was 9 inches. Hence, the value 9 represents the initial length of the vine plant.
Step 3: Eliminate the incorrect answer choices
Now let’s evaluate each answer choice in the context of the problem:
A) Tavon will keep the vine plant for 9 months.
Incorrect: The value 9 represents an initial length, not a time duration. There’s no mention of how long Tavon will keep the plant in the equation.
B) The vine plant is expected to grow 9 inches each month.
Incorrect: The growth rate is represented by the coefficient of t, which is 14, not 9. This suggests the plant grows 14 inches per month, not 9.
C) The vine plant is expected to grow to a maximum length of 9 inches.
Incorrect: The length of the plant increases as t increases, with no maximum length indicated by the function. The value 9 refers to the initial length, not a maximum length.
D) The estimated length of the vine plant was 9 inches when Tavon purchased it.
Correct: This aligns with the interpretation of b = 9 as the initial length of the plant when t = 0.
Step 4: Verify the Answer
Substituting t = 0 into the function gives f(0) = 9, confirming that the initial length of the plant was indeed 9 inches.
Final Answer: Option D.
7th Question
(x + 2)(x – 5)(x + 9) = 0
Question: What is a positive solution to the given equation?
A) 3
B) 4
C) 5
D) 18
Choice C is correct. Applying the zero product property to the given equation yields three equations: x + 2 = 0, x – 5 = 0, and x + 9 = 0. Subtracting 2 from both sides of the equation x + 2 = 0 yields x = -2. Adding 5 to both sides of the equation x – 5 = 0 yields x = 5. Subtracting 9 from both sides of the equation x + 9 = 0 yields x = -9. Therefore, the solutions to the given equation are -2, 5, and -9. It follows that a positive solution to the given equation is 5.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understanding the equation
This is a factored equation of the form:
A ⋅ B ⋅ C = 0
where A = (x + 2), B = (x − 5), and C = (x + 9).
For a product to equal zero, at least one of the factors must equal zero:
x + 2 = 0, x − 5 = 0, x + 9 = 0
Step 2: Solve for x
We solve each equation individually:
1) From x + 2 = 0:
Subtract 2 from both sides:
x = −2
2) From x − 5 = 0:
Add 5 to both sides:
x = 5
3) From x + 9 = 0:
Subtract 9 from both sides:
x = −9
Step 3: Identify the positive solution
The solutions to the equation are:
x = −2, x = 5, x = −9
Among these, the only positive value is:
x = 5
Step 4: Verify the solution
Substitute x = 5 into the original equation to verify:
(x + 2)(x − 5)(x + 9) = (5 + 2)(5 − 5)(5 + 9)
= 7 ⋅ 0 ⋅ 14 = 0
The equation holds true, confirming that x = 5 is a solution.
Final Answer: C) 5.
8th Question
Question: Brian saves 2/5 of the $215 he earns each week from his job. If Brian continues to save at this rate, how much money, in dollars, will Brian save in 9 weeks?
A) 430
B) 86
C) 9
D) 774
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 774. It’s given that Brian saves 2/5 of the $215 he earns each week from his job. Therefore, Brian saves (2/5)($215), or $86, per week. If Brian continues to save at this rate of $86 per week for 9 weeks, then he will save a total of (9)(86), or 774, dollars.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step 1: Calculate the weekly savings
Brian saves 2/5 of his weekly earnings, which is $215.
To calculate his weekly savings, multiply his earnings by the fraction he saves:
Weekly savings = 2/5 × 215
Simplify the multiplication:
1) Divide 215 by 5: 215 ÷ 5 = 43
2) Multiply the result by 2: 43 × 2 = 86
Thus, Brian saves $86 per week.
Step 2: Calculate total savings for 9 weeks
To find the total amount Brian saves in 9 weeks, multiply his weekly savings by 9:
Total savings = 86 × 9
Simplify the multiplication:
1) Break down 86 × 9 for easier computation:
86 × 9 = (80 + 6) × 9
= (80 × 9) + (6 × 9)
2) Calculate each term: 80 × 9 = 720, 6 × 9 = 54
3) Add the results: 720 + 54 = 774
Thus, Brian saves $774 in 9 weeks.
Step 3: Verify the calculations
1) Weekly savings: 2/5 × 215 = 86 (confirmed)
2) Total savings: 86 × 9 = 774 (confirmed)
Final Answer: Brian will save $774 in 9 weeks: 774.
9th Question
Question: A rectangle has an area of 155 square inches. The length of the rectangle is 4 inches less than 7 times the width of the rectangle. What is the width of the rectangle, in inches?
A) 4
B) 5
C) 7
D) 11
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 5. Let x represent the width, in inches, of the rectangle. It’s given that the length of the rectangle is 4 inches less than 7 times its width, or 7x – 4 inches. The area of a rectangle is equal to its width multiplied by its length. Multiplying the width, x inches, by the length, 7x – 4 inches, yields x(7x – 4) square inches. It’s given that the rectangle has an area of 155 square inches, so it follows that x(7x – 4) = 155, or 7x2 – 4x = 155. Subtracting 155 from both sides of this equation yields 7x2 – 4x – 155 = 0. Factoring the left-hand side of this equation yields (7x + 31)(x – 5) = 0. Applying the zero product property to this equation yields two solutions: x = -31/7 and x = 5. Since x is the rectangle’s width, in inches, which must be positive, the value of x is 5. Therefore, the width of the rectangle, in inches, is 5.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
There are two methods to solve this.
1) Quadratic Formula
2) Factoring Formula
1) Quadratic Formula
Step 1: Define the variables
Let:
~ w = the width of the rectangle (in inches),
~ l = the length of the rectangle (in inches).
From the problem, the area of the rectangle is given as:
Area = length × width = l × w
and the length l is expressed in terms of the width:
l = 7w − 4
Substitute l = 7w − 4 into the area equation:
Area = (7w − 4) ⋅ w
Step 2: Write and simplify the equation
The area of the rectangle is given as 155 in2:
(7w − 4) ⋅ w = 155
Simplify the equation:
7w2 − 4w = 155
Rearrange the equation into standard quadratic form:
7w2 − 4w − 155 = 0
Step 3: Solve the quadratic equation

Since the width of a rectangle cannot be negative, we reject w = −31/7 and accept w = 5.
Step 4: Verify the solution
If w = 5, then the length is:
l = 7w − 4
= 7(5) − 4
= 35 − 4 = 31
The area of the rectangle is:
Area = l ⋅ w
= 31 ⋅ 5 = 155 in2
This matches the given area, so the solution is correct.
Final Answer: The width of the rectangle is: 5 inches.
2) Factoring Formula
Step 1: Solve by factoring
We need to factor 7w2 − 4w − 155. First, identify the coefficients:
~ a = 7, b = −4, c = −155.
To factor the quadratic expression, find two numbers whose:
~ Product = a ⋅ c = 7 ⋅ (−155) = −1085,
~ Sum = b = −4.
The two numbers are 31 and −35, because:
31 ⋅ (−35) = −1085 and 31 + (−35) =−4
Step 3: Rewrite and group
Rewrite the quadratic equation using these numbers to split the middle term:
7w2 − 35w + 31w − 155 = 0
Group the terms into two pairs:
(7w2 − 35w) + (31w − 155) = 0
Factor out the greatest common factor (GCF) from each group:
7w(w − 5) + 31(w − 5) = 0
Step 4: Factor the common binomial
Factor out (w − 5):
(7w + 31)(w − 5) = 0
Step 5: Solve for w
Using the zero-product property, set each factor equal to 0:
1) 7w + 31 = 0:
7w = −31
⇒ w = −31/7
(Since width cannot be negative, discard this solution.)
2) w − 5 = 0:
w = 5.
Step 6: Verify the solution
If w = 5, then the length is:
l = 7w − 4 = 7(5) − 4 = 31
The area is:
Area = l ⋅ w = 31 ⋅ 5 = 155 in2
This matches the given area, so the solution is correct.
Final Answer: The width of the rectangle is: 5 inches.
10th Question
4, 10, 18, 4, 4, 5, 6, 5
Question: What is the median of the data set shown?
A) 4
B) 5
C) 7
D) 14
Choice B is correct. If a data set contains an even number of data values, when the data values are listed in ascending or descending order, the median is between the two middle values. The given data set contains 8 values. When listed in ascending order, the data set is 4, 4, 4, 5, 5, 6, 10, 18 and the two middle values are 5 and 5. Since the two middle values are the same, the median must be 5.
Choice A is incorrect. This value is between the two middle values in the list shown, not the two middle values when the data values are listed in ascending or descending order.
Choice C is incorrect. This is the mean, not the median, of the data set.
Choice D is incorrect. This is the range, not the median, of the data set.
Step 1: Understand the median
The median is the middle value of a data set when the numbers are arranged in increasing order. If there is an odd number of data points, the median is the middle value. If there is an even number of data points, the median is the average of the two middle values.
Step 2: Arrange the data in increasing order
The data set is:
4, 10, 18, 4, 4, 5, 6, 5
Arrange it in increasing order:
4, 4, 4, 5, 5, 6, 10, 18
Step 3: Determine the number of data points
There are 8 data points in the data set, which is an even number. Therefore, the median will be the average of the two middle values.
Step 4: Identify the two middle values
The two middle values are the 4th and 5th numbers in the ordered list:
4, 4, 4, 5, 5, 6, 10, 18
Step 5: Calculate the median
The two middle values are 5 and 5. The average of these values is:
Median = 5 + 5/2
= 10/2 = 5
Step 6: Final Answer: The median of the data set is: 5.
11th Question
g(x) = x2 + 55
Question: What is the minimum value of the given function?
A) 0
B) 55
C) 110
D) 3,025
Choice B is correct. For a quadratic function defined by an equation of the form g(x) = a(x – h)2 + k, where a, h, and k are constants and a > 0, the minimum value of the function is k. In the given function, a = 1, h = 0, and k = 55. Therefore, the minimum value of the given function is 55.
Choice A is incorrect. This is the value of x for which the given function reaches its minimum value, not the minimum value of the function.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the given function
The function is:
g(x) = x2 + 55
This is a quadratic function, and its graph is a parabola that opens upwards because the coefficient of x2 (which is 1) is positive.
For such a parabola, the minimum value occurs at the vertex of the parabola.
Step 2: Find the vertex
The general form of a quadratic equation is:
g(x) = ax2 + bx + c
Here:
~ a = 1,
~ b = 0, and
~ c = 55.
The x-coordinate of the vertex is given by:
x = −b/2a
Substitute b = 0 and a = 1:
x = −0/2(1) = 0
Step 3: Find the minimum value
The minimum value of the function occurs at x = 0. Substitute x = 0 into the function g(x):
g(0) = (0)2 + 55 = 55
Thus, the minimum value of the function is: 55.
Step 4: Explanation
The parabola opens upwards because the coefficient of x2 is positive. The constant 55 represents the vertical shift of the parabola, ensuring that its minimum value is 55 when x = 0.
How do we know, it’s a parabola?
A parabola is the graph of any quadratic function, which has the general form:
f(x) = ax2 + bx + c
Here’s how we know that g(x) = x2 + 55 is a parabola.
~ If a > 0, the parabola opens upward (a “U” shape).
~ If a < 0, the parabola opens downward (an upside-down “U” shape).
How do we know it’s a quadratic equation?
The given function is: g(x) = x2 + 55
The highest power of x is 2.
When a function includes x2 as the term with the highest degree, it is classified as a quadratic equation. In this case, x2 is the leading term, making g(x) a quadratic function.
Final Answer: B) 55.
12th Question
Question: Each year, the value of an investment increases by 0.49% of its value the previous year. Which of the following functions best models how the value of the investment changes over time?
A) Decreasing exponential
B) Decreasing linear
C) Increasing exponential
D) Increasing linear
Choice C is correct. Because the value of the investment increases each year, the function that best models how the value of the investment changes over time is an increasing function. It′s given that each year, the value of the investment increases by 0.49% of its value the previous year. Since the value of the investment changes by a fixed percentage each year, the function that best models how the value of the investment changes over time is an exponential function. Therefore, the function that best models how the value of the investment changes over time is an increasing exponential function.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Understanding the Question
The problem involves the yearly growth of an investment at a rate of 0.49%. The goal is to identify the type of function that best represents how the investment value changes over time.
Breaking It Down
1) How does the investment change each year?
~ Each year, the investment increases by 0.49% of its value the previous year.
~ This means the value of the investment for the next year depends on its value in the current year. The new value is calculated as:
New Value = Current Value × (1 + 0.0049)
~ Let’s model this mathematically:
~ ~ If the initial investment value is V0, then:
~ ~ ~ After 1 year: V1 = V0 × 1.0049,
~ ~ ~ After 2 years: V2 = V1 × 1.0049 = V0 × 1.00492,
~ ~ ~ After t years: Vt = V0 × 1.0049t.
2) What does this equation represent?
The equation Vt = V0 × 1.0049t is an exponential function, where the base 1.0049 represents the growth factor, and t is the number of years.
Analyzing the Choices
Option A: Decreasing exponential
~ A decreasing exponential function occurs when the base of the exponential term is between 0 and 1 (e.g., Vt = V0 × (0.8)t).
~ This does not apply here because the investment is increasing, not decreasing.
Option B: Decreasing linear
~ A decreasing linear function would look like Vt = V0 − kt, where the value decreases by the same fixed amount (k) every year.
~ This is incorrect because the investment is growing, not shrinking, and the growth is not constant but proportional.
Option C: Increasing exponential
~ An increasing exponential function occurs when the base of the exponential term is greater than 1 (e.g., Vt = V0 × (1.0049)t).
~ This matches the situation described in the problem since the investment grows by 0.49% each year, making 1.0049 the growth factor.
Option D: Increasing linear
~ An increasing linear function would look like Vt = V0 + kt, where the value increases by the same fixed amount (k) every year.
~ This is incorrect because the growth in this case is proportional to the current value, not constant.
Correct Answer
The correct choice is: C) Increasing exponential.
13th Question
Question: The population of Greenville increased by 7% from 2015 to 2016. If the 2016 population is k times the 2015 population, what is the value of k?
A) 0.07
B) 0.7
C) 1.07
D) 1.7
Choice C is correct. Let x be the 2015 population of Greenville. It’s given that the population increased by 7% from 2015 to 2016. The increase in population can be written as (0.07)x. The 2016 population of Greenville is given as the sum of the 2015 population of Greenville and the increase in population from 2015 to This can be rewritten as x + (0.07)x, or 1.07x. Therefore, the value of k is 1.07.
Choice A is incorrect. This is the percent, represented as a decimal, that the population increased from 2015 to 2016, not the value of k.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the value of k if the population increased by 70%, not 7%, from 2015 to 2016.
Understanding the Question
The problem describes an increase in population by 7% from 2015 to 2016. The goal is to determine the value of k, which represents the ratio of the 2016 population to the 2015 population. Essentially, we need to find how many times larger the 2016 population is compared to the 2015 population.
Step-by-Step Explanation
1) Define the Population Variables
~ Let the population of Greenville in 2015 be P2015.
~ The population in 2016, P2016, increased by 7% compared to 2015. This means:
P2016 = P2015 + 0.07 × P2015
2) Factorize the Expression
~ Combine like terms: P2016 = P2015(1 + 0.07)
Simplify:
P2016 = P2015 × 1.07
3) Interpret k
~ The value of k is the ratio of the 2016 population to the 2015 population:
k = P2016/P2015
~ Substituting P2016 = P2015 × 1.07:
k = 1.07
Analyzing the Answer Choices
Option A: 0.07
This represents only the percentage increase (7%) in decimal form, not the total ratio of the populations. Incorrect.
Option B: 0.7
This represents a much smaller ratio (less than 1), implying the population decreased, which is not the case. Incorrect.
Option C: 1.07
This is correct because it represents the total ratio: the 2016 population is 1.07 times the 2015 population.
Option D: 1.7
This would indicate a 70% increase in population, which is not supported by the problem. Incorrect.
Correct Answer: The correct choice is: C) 1.07.
14th Question
Question: The function f(x) = 1/9(x − 7)2 + 3 gives a metal ball’s height above the ground f(x), in inches, x seconds after it started moving on a track, where 0 ≤ x ≤ 10. Which of the following is the best interpretation of the vertex of the graph of y = f(x) in the xy-plane?
A) The metal ball’s minimum height was 3 inches above the ground.
B) The metal ball’s minimum height was 7 inches above the ground.
C) The metal ball’s height was 3 inches above the ground when it started moving.
D) The metal ball’s height was 7 inches above the ground when it started moving.
Choice A is correct. The graph of a quadratic equation in the form y = a(x – h)2 + k, where a, h, and k are positive constants, is a parabola that opens upward with vertex (h, k). The given function f(x) = 1/9(x – 7)2 + 3 is in the form y = a(x – h)2 + k, where y = f(x), a = 1/9, h = 7, and k = 3. Therefore, the graph of y = f(x) is a parabola that opens upward with vertex (7, 3). Since the parabola opens upward, the vertex is the lowest point on the graph. It follows that the y-coordinate of the vertex of the graph of y = f(x) is the minimum value of f(x). Therefore, the minimum value of f(x) is 3. It’s given that f(x) = 1/9(x – 7)2 + 3 represents the metal ball’s height above the ground, in inches, x seconds after it started moving on a track. Therefore, the best interpretation of the vertex of the graph of y = f(x) is that the metal ball’s minimum height was 3 inches above the ground.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Question Analysis:
We are given the quadratic function f(x) = 1/9(x − 7)2 + 3, which represents the height of a metal ball above the ground over time, and we need to interpret the vertex of the parabola formed by this function.
Step-by-Step Solution:
1) Form of the Function:
The function is given in vertex form:
f(x) = a(x − h)2 + k
Here:
~ (h, k) represents the vertex of the parabola.
~ a > 0, so the parabola opens upwards, meaning the vertex is the minimum point of the graph.
2. Identify the Vertex:
From the function f(x) = 1/9(x − 7)2 + 3:
~ h = 7: The x-coordinate of the vertex is 7 seconds.
~ k = 3: The y-coordinate of the vertex is 3 inches.
Thus, the vertex of the parabola is at (7, 3).
3. Interpret the Vertex:
The vertex represents the minimum height of the ball, which occurs when x = 7. This means:
~ The minimum height of the metal ball above the ground is 3 inches.
4. Analyze the Answer Choices:
A) The metal ball’s minimum height was 3 inches above the ground.
~ Correct. This matches the interpretation of the vertex.
B) The metal ball’s minimum height was 7 inches above the ground.
~ Incorrect. The height is 3 inches, not 7 inches.
C) The metal ball’s height was 3 inches above the ground when it started moving.
~ Incorrect. At x = 0, the height can be calculated as f(0) = 1/9(0 − 7)2 + 3 = 49/9 + 3 ≠ 3.
D) The metal ball’s height was 7 inches above the ground when it started moving.
~ Incorrect. At x = 0, the height is greater than 3 inches and not 7 inches.
Verification:
At x = 7, substituting into f(x):
f(7) = 1/9(7 − 7)2 + 3 = 3
This confirms the minimum height is 3 inches.
Final Answer: Option A.
15th Question
Question: In triangle JKL, cos(K) = 24/51 and angle J is a right angle. What is the value of cos(L)?
A) 24/15
B) 15/17
C) 42/51
D) 51/24
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 15/17. It’s given that angle J is the right angle in triangle JKL. Therefore, the acute angles of triangle JKL are angle K and angle L. The hypotenuse of a right triangle is the side opposite its right angle. Therefore, the hypotenuse of triangle JKL is side KL. The cosine of an acute angle in a right triangle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. It’s given that cos(K) = 24/51. This can be written as cos(K) = 8/17. Since the cosine of angle K is a ratio, it follows that the length of the side adjacent to angle K is 8n and the length of the hypotenuse is 17n, where n is a constant. Therefore, JK = 8n and KL = 17n. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. For triangle JKL, it follows that (JK)2 + (JL)2 = (KL)2 . Substituting 8n for JK and 17n for KL yields (8n)2 + (JL)2 = (17n)2. This is equivalent to 64n2 + (JL)2 = 289n2. Subtracting 64n2 from each side of this equation yields (JL)2 = 225n2. Taking the square root of each side of this equation yields JL = 15n. Since cos(L) = JL/KL, it follows that cos(L) = 15n/17n, which can be rewritten as cos(L) = 15/17. Note that 15/17, .8824, .8823, and 0.882 are examples of ways to enter a correct answer.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Question Analysis:
We are asked to determine the value of cos(L) in a right triangle JKL, where:
~ cos(K) = 24/51
~ ∠J is the right angle.
Since ∠J is 90∘, the other two angles K and L are complementary:
K + L = 90∘
This means:
cos(L) = sin(K)
Step-by-Step Solution:
1. Recall the Relationship Between Complementary Angles:
In a right triangle:
cos(Angle) = sin(Complementary Angle)
Thus, cos(L) = sin(K).
2. Use the Given Value of cos(K):
We know:
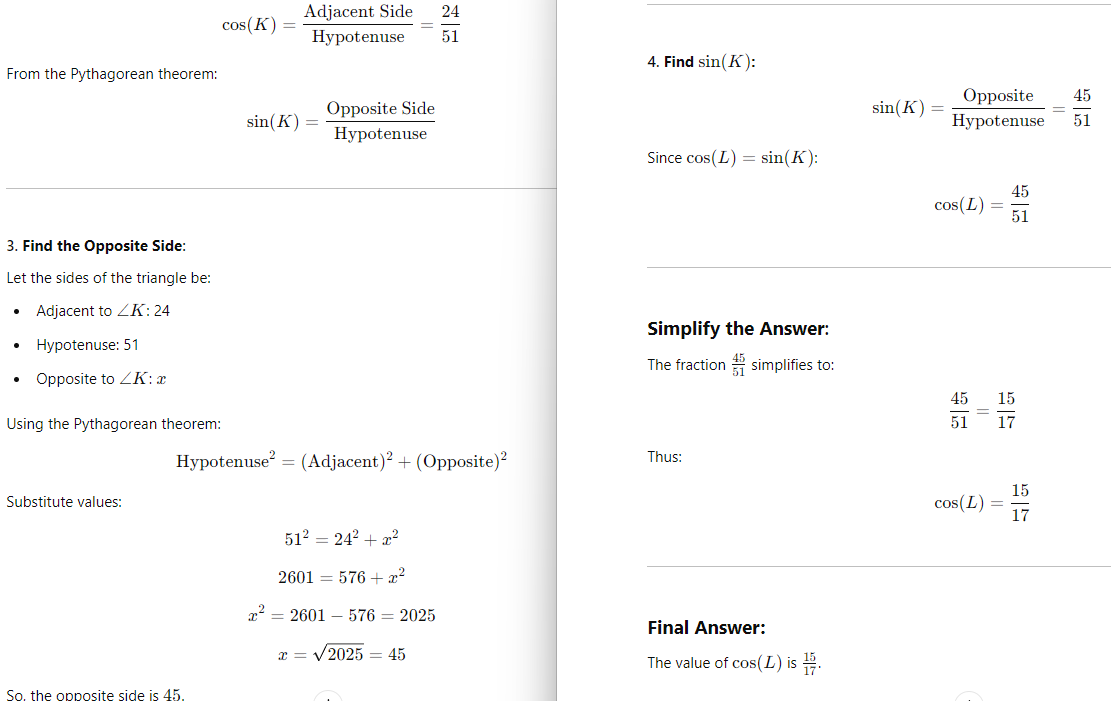
Final Answer: Option B.
16th Question
Question: If |4x − 4| = 112, what is the positive value of x − 1?
A) 112
B) -112
C) -28
D) 28
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 28. The given absolute value equation can be rewritten as two linear equations: 4x – 4 = 112 and -(4x – 4) = 112, or 4x – 4 = -112. Adding 4 to both sides of the equation 4x – 4 = 112 results in 4x = 116. Dividing both sides of this equation by 4 results in x = 29. Adding 4 to both sides of the equation 4x – 4 = -112 results in 4x = -108. Dividing both sides of this equation by 4 results in x = -27. Therefore, the two values of x – 1 are 29 – 1, or 28, and -27 – 1, or -28. Thus, the positive value of x – 1 is 28.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Understanding the Problem
The equation given is:
∣4x − 4∣ = 112
We are tasked with finding the positive value of x − 1.
What Does | | Represent?
The symbol | | represents the absolute value of an expression. The absolute value of a number or expression is its distance from 0 on the number line, so it is always non-negative. For example:
∣5∣ = 5
∣−5∣ = 5
This means:
∣4x − 4∣ = 112
can represent two possible cases:
1) 4x − 4 = 112
2) 4x − 4 = −112
We will solve both cases to find all possible solutions for x.
Step-by-Step Solution
Case 1: 4x − 4 = 112
1) Add 4 to both sides: 4x = 112 + 4
4x = 116
2) Divide by 4: x = 116/4 = 29
Case 2: 4x − 4 = −112
1) Add 4 to both sides: 4x = −112 + 4
4x = −108
2) Divide by 4: x = −108/4 = −27
Determine the Value of x − 1:
We now calculate x − 1 for both values of x:
1) When x = 29:
x − 1 = 29 − 1 = 28
2) When x = −27:
x − 1 = −27 − 1 = −28
Since we are asked for the positive value of x − 1:
The positive value is 28.
Verify the Solution:
Substitute both x = 29 and x = −27 back into the original equation to verify:
1) For x = 29:
∣4x − 4∣ = ∣4(29) − 4∣ = ∣116 − 4∣ = ∣112∣ = 112
2) For x = −27:
∣4x − 4∣ = ∣4(−27) − 4∣ = ∣−108 − 4∣ = ∣−112∣ = 112
Both values satisfy the equation.
Final Answer: The positive value of x − 1 is: 28.
17th Question
Question: A cube has an edge length of 68 inches. A solid sphere with a radius of 34 inches is inside the cube, such that the sphere touches the center of each face of the cube. To the nearest cubic inch, what is the volume of the space in the cube not taken up by the sphere?
A) 149,796
B) 164,500
C) 190,955
D) 310,800
Choice A is correct. The volume of a cube can be found by using the formula V = s3, where V is the volume and s is the edge length of the cube. Therefore, the volume of the given cube is V = 683, or 314,432 cubic inches. The volume of a sphere can be found by using the formula V = 4πr3/3, where V is the volume and r is the radius of the sphere. Therefore, the volume of the given sphere is V = 4π/3(34)3, or approximately 164,636 cubic inches. The volume of the space in the cube not taken up by the sphere is the difference between the volume of the cube and the volume of the sphere. Subtracting the approximate volume of the sphere from the volume of the cube gives 314,432 – 164,636 = 149,796 cubic inches.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understanding the Problem
We are tasked with finding the volume of the space inside a cube that is not occupied by a sphere. Here’s what we know:
~ The cube has an edge length of 68 inches.
~ A sphere with a radius of 34 inches is perfectly inscribed inside the cube. This means the sphere touches the center of each face of the cube.
~ To find the remaining space:
Remaining volume = Volume of the cube − Volume of the sphere.
Step 2: Volume of the Cube
The formula for the volume of a cube is:
Vcube = 683
~ The edge length of the cube is 68 inches.
~ Substitute 68 into the formula: Vcube = 683
Perform the calculation:
683 = 68 × 68 × 68
1) First, calculate 68 × 68 = 4,624.
2) Then multiply 4,624 × 68 = 314,432.
So, the volume of the cube is:
Vcube = 314,432 cubic inches.
Step 3: Volume of the Sphere
The formula for the volume of a sphere is:

Step 4: Calculate the Remaining Volume
The remaining volume is the difference between the volume of the cube and the volume of the sphere:
Remaining volume = Vcube − Vsphere
Substitute the values:
Remaining volume = 314,432 − 164,636.6
Perform the subtraction:
Remaining volume = 149,795.4 cubic inches.
Final Answer:
The volume of the space in the cube not taken up by the sphere is approximately: A) 149,795 cubic inches.
18th Question
Question: What is the diameter of the circle in the xy-plane with equation (x − 5)2 + (y − 3)2 = 16?
A) 4
B) 8
C) 16
D) 32
Choice B is correct. The standard form of an equation of a circle in the xy-plane is (x – h)2 + (y – k)2 = r2, where the coordinates of the center of the circle are (h, k) and the length of the radius of the circle is r. For the circle in the xy-plane with equation (x – 5)2 + (y – 3)2 = 16, it follows that r2 = 16. Taking the square root of both sides of this equation yields r = 4 or r = -4. Because r represents the length of the radius of the circle and this length must be positive, r = 4. Therefore, the radius of the circle is 4. The diameter of a circle is twice the length of the radius of the circle. Thus, 2(4) yields 8. Therefore, the diameter of the circle is 8.
Choice A is incorrect. This is the radius of the circle.
Choice C is incorrect. This is the square of the radius of the circle.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Equation of a Circle
The standard equation of a circle in the xy-plane is:
(x − h)2 + (y − k)2 = r2
Here:
~ (h, k) is the center of the circle.
~ r is the radius of the circle.
~ r2 is the square of the radius.
The given equation of the circle is:
(x − 5)2 + (y − 3)2 = 16
Step 2: Identify Key Components of the Circle
From the equation:
1) Compare it with the standard equation (x − h)2 + (y − k)2 = r2:
~ h = 5: The x-coordinate of the center.
~ k = 3: The y-coordinate of the center.
~ r2 = 16: The square of the radius.
2) Find the radius r by taking the square root of r2:
r = square root of 16 is = 4.
Step 3: Diameter of the Circle
The diameter of a circle is twice its radius:
Diameter = 2 × r
Substitute r = 4:
Diameter = 2 × 4 = 8
Step 4: Verify the Solution
To ensure the solution is accurate:
~ The equation (x − 5)2 + (y − 3)2 = 16 fits the standard form of a circle.
~ r2 = 16 confirms that r = 4.
~ Using the formula for diameter (2r), the calculation 2 × 4 = 8 is correct.
Final Answer: The diameter of the circle is: 8 units.
19th Question
Question: For the exponential function f, the value of f(1) is k, where k is a constant. Which of the following equivalent forms of the function f shows the value of k as the coefficient or the base?
A) f(x) = 50(1.6)x+1
B) f(x) = 80(1.6)x
C) f(x) = 128(1.6)x – 1
D) f(x) = 204.8(1.6)x – 2
Choice C is correct. For the form of the function in choice C, f(x) = 128(1.6)x – 1, the value of f(1) can be found as 128(1.6)1 – 1, which is equivalent to 128(1.6)0, or Therefore, k = 128, which is shown in f(x) = 128(1.6)x – 1 as the coefficient.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Problem
We are given:
1) The exponential function f(x).
2) The value f(1) = k, where k is a constant.
3) We need to determine which of the given forms of f(x) clearly shows the value of k as either the coefficient or the base.
An exponential function typically has the form:
f(x) = a ⋅ bx
Where:
~ a is the initial value (when x = 0).
~ b is the base (growth or decay factor).
Step 2: Evaluate Each Option
We will substitute x = 1 into each given option and calculate f(1) to identify which form matches f(1) = k.
Option A: f(x) = 50(1.6)x + 1
Substitute x = 1:
f(1) = 50(1.6)1 + 1 = 50(1.6)2
Calculate (1.6)2:
(1.6)2 = 2.56
Substitute back: f(1) = 50 ⋅ 2.56 = 128
So, k =128 for this form.
Option B: f(x) = 80(1.6)x
Substitute x = 1:
f(1) = 80(1.6)1 = 80 ⋅ 1.6 = 128
So, k = 128 for this form as well.
Option C: f(x) = 128(1.6)x – 1
Substitute x = 1:
f(1) = 128(1.6)1 – 1 = 128(1.6)0 = 128 ⋅ 1 = 128
So, k = 128 for this form too.
Option D: f(x) = 204.8(1.6)x – 2
Substitute x = 1:
f(1) = 204.8(1.6)1 – 2 = 204.8(1.6)-1
Calculate (1.6)-1:
(1.6)-1 = 1/1.6 = 0.625
Substitute back:
f(1) = 204.8 ⋅ 0.625 = 128
So, k = 128 for this form as well.
Step 3: Identify the Form That Shows k
We know k = 128 from all options. Now, we examine the forms to see which explicitly shows k as either:
~ The coefficient (a).
~ The base (b).
Option C: f(x) = 128(1.6)x – 1
Here, k = 128 is directly the coefficient, making it the clearest representation of k.
Final Answer: C) f(x) = 128(1.6)x – 1.
20th Question
Question: A model estimates that at the end of each year from 2015 to 2020, the number of squirrels in a population was 150% more than the number of squirrels in the population at the end of the previous year. The model estimates that at the end of 2016, there were 180 squirrels in the population. Which of the following equations represents this model, where n is the estimated number of squirrels in the population t years after the end of 2015 and t ≤ 5?
A) n = 72(1.5)t
B) n = 72(2.5)t
C) n = 180(1.5)t
D) n = 180(2.5)t
Choice B is correct. Since the model estimates that the number of squirrels in the population increased by a fixed percentage, 150%, each year, the model can be represented by an exponential equation of the form n = a(1 + p/100)t, where a is the estimated number of squirrels in the population at the end of 2015, and the model estimates that at the end of each year, the number is p% more than
the number at the end of the previous year. Since the model estimates that at the end of each year, the number was 150% more than the number at the end of the previous year, p = 150. Substituting 150 for p in the equation n = a(1 + p/100)t yields n = a(1 + 150/100)t, which is equivalent to n = a(1 + 1.5)t, or a(2.5)t. It’s given that the estimated number of squirrels at the end of 2016 was 180. This means that when t = 1, n = 180. Substituting 1 for t and 180 for n in the equation n = a(2.5)t yields 180 = a(2.5)1, or 180 = 2.5a. Dividing each side of this equation by 2.5 yields 72 = a. Substituting 72 for a in the equation n = a(2.5)t yields n = 72(2.5)t.
Choice A is incorrect. This equation represents a model where at the end of each year, the estimated number of squirrels was 150% of, not 150% more than, the estimated number at the end of the previous year.
Choice C is incorrect. This equation represents a model where at the end of each year, the estimated number of squirrels was 150% of, not 150% more than, the estimated number at the end of the previous year, and the estimated number of squirrels at the end of 2015, not the end of 2016, was 180.
Choice D is incorrect. This equation represents a model where the estimated number of squirrels at the end of 2015, not the end of 2016, was 180.
Step 1: Understand the Problem
We are given:
1) Population growth rate: At the end of each year, the population increases by 150% of the previous year’s population.
~ This means the population is multiplied by 1 + 1.5 = 2.5 each year.
2) 2016 Population: The population at the end of 2016 was 180 squirrels.
3) Model: The equation must represent the population n after t years, where t = 0 corresponds to the end of 2015.
We need to find the equation for n, given this growth pattern.
Step 2: General Form of the Equation
For exponential growth, the general form of the equation is:
n = n0 ⋅ rt
Where:
~ n0: Initial population (at t = 0).
~ r: Growth factor per year.
~ t: Time in years after the starting year (2015 in this case).
From the problem:
~ The growth factor r = 2.5 (population increases by 150% each year).
~ t = 0: Represents the population at the end of 2015.
Step 3: Determine n0 Using 2016 Population
At the end of 2016 (t = 1), the population is n = 180. Substituting into the general equation:
n = n0 ⋅ 2.5t
For t = 1:
180 = n0 ⋅ 2.51
180 = n0 ⋅ 2.5
Solve for n0:
n0 = 180/2.5 = 72
Thus, the initial population at the end of 2015 is n0 = 72.
Step 4: Write the Full Equation
Substitute n0 = 72 and r = 2.5 into the general equation:
n = 72 ⋅ 2.5t
Step 5: Verify the Answer
Let’s check if this equation works for t = 1:
n = 72 ⋅ 2.51 = 72 ⋅ 2.5 = 180
This matches the given population for 2016, so the equation is correct.
Final Answer: B) n = 72(2.5)t.
Explanation of Incorrect Choices:
Option A) n = 72(1.5)t:
~ This uses the wrong growth factor (1.5 instead of 2.5).
~ Growth of 150% means the population is multiplied by 2.5, not 1.5.
Option C) n = 180(1.5)t:
~ This uses the wrong initial population (180 instead of 72) and the wrong growth factor.
Option D) n = 180(2.5)t:
~ This uses the wrong initial population (180 instead of 72).
21th Question
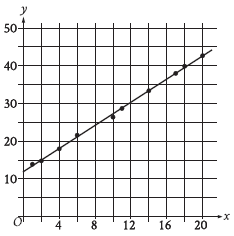
Question: The scatterplot shows the relationship between two variables, x and y, for data set E. A line of best fit is shown. Data set F is created by multiplying the y-coordinate of each data point from data set E by 3.9. Which of the following could be an equation of a line of best fit for data set F?
A) y = 46.8 + 5.9x
B) y = 46.8 + 1.5x
C) y = 12 + 5.9x
D) y = 12 + 1.5x
Choice A is correct. An equation of a line of best fit for data set F can be written in the form y = a + bx, where a is the y-coordinate of the y-intercept of the line of best fit and b is the slope. The line of best fit shown for data set E has a y-intercept at approximately (0, 12). It’s given that data set F is created by multiplying the y-coordinate of each data point from data set E by 3.9. It follows that a line of best fit for data set F has a y-intercept at approximately [0, 12(3.9)], or (0, 46.8). Therefore, the value of a is approximately 46.8. The slope of a line that passes through points (x1, y1) and (x2, y2) can be calculated as y2 – y1/x2 – x1. Since the line of best fit shown for data set E passes approximately through the point (12, 30), it follows that a line of best fit for data set F passes approximately through the point (12, 30(3.9)], or (12, 117). Substituting (0, 46.8) and (12, 117) for (x1, y1) and (x2, y2), respectively, in y2 – y1/x2 – x1 yields 117 – 46.8/12 – 0, which is equivalent to 70.2/12, or 5.85. Therefore, the value of b is approximately 5.85, or approximately 5.9. Thus, y = 46.8 + 5.9x could be an equation of a line of best fit for data set F.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This could be an equation of a line of best fit for data set E, not data set F.
Step 1: Understand the Problem
1) Scatterplot: The scatterplot shows the relationship between xxx and y for data set E, with a line of best fit drawn.
2) Data set F: Created by multiplying the y-coordinates of each data point in data set E by 3.9.
3) Task: Find an equation of the line of best fit for data set F.
Step 2: Relationship Between Data Sets E and F
For data set F, the transformation involves scaling the y-coordinate of every point in data set E by 3.9. This means:
~ The slope of the line of best fit for data set F will also be scaled by 3.9 because slopes are ratios of y-changes to x-changes.
~ The y-intercept of the line of best fit for data set F will also be scaled by 3.9 because it is a y-coordinate.
Step 3: Analyze the Line of Best Fit for Data Set E
From the graph of data set E:
~ The line of best fit appears to have a y-intercept of 12 and a slope of 1.5.
The equation for the line of best fit for data set E is:
y = 12 + 1.5x
Step 4: Apply the Transformation for Data Set F
1) Multiply the y-intercept of 12 by 3.9:
12 ⋅ 3.9 = 46.8
2) Multiply the slope of 1.5 by 3.9:
1.5 ⋅ 3.9 = 5.9
Thus, the equation of the line of best fit for data set F is:
y = 46.8 + 5.9x
Step 5: Verify the Answer
The equation y = 46.8 + 5.9x satisfies the transformation rule, as both the slope and the intercept are scaled by 3.9. Let’s check if any other option matches:
A) y = 46.8 + 5.9x: Correct.
B) y = 46.8 + 1.5x: Incorrect, as the slope is not scaled.
C) y = 12 + 5.9x: Incorrect, as the intercept is not scaled.
D) y = 12 + 1.5x: Incorrect, as neither the slope nor the intercept is scaled.
Final Answer: The correct answer is: A) y = 46.8 + 5.9x.
22th Question
48x – 64y = 48y + 24
ry = 1/8 – 12x
Question: In the given system of equations, r is a constant. If the system has no solution, what is the value of r?
A) -28
B) 28
C) 24
D) -24
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A: The correct answer is -28. A system of two linear equations in two variables, x and y, has no solution if the lines represented by the equations in the xy-plane are distinct and parallel. The graphs of two lines in the xy-plane represented by equations in the form Ax + By = C, where A, B, and C are constants, are parallel if the coefficients for x and y in one equation are proportional to the corresponding coefficients for x and y in the other equation. The first equation in
the given system, 48x – 64y = 48y + 24, can be written in the form Ax + By = C by subtracting 48y from both sides of the equation to yield 48x – 112y = 24. The second equation in the given system, ry = 1/8 – 12x, can be written in the form Ax + By = C by adding 12x to both sides of the equation to yield 12x + ry = 1/8. The coefficient of x in the second equation is 1/4 times the coefficient of x in the first
equation. That is, 48(1/4) = 12. For the lines to be parallel, the coefficient of y in the second equation must also be 1/4 times the coefficient of y in the first equation. Therefore, -112(1/4) = r, or -28 = r. Thus, if the given system has no solution, the value of r is -28.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
We are told that the system has no solution, and we need to determine the value of the constant r.
Step 1: Rearrange and simplify the equations

Step 2: Interpret the condition for “no solution”
For a system of linear equations to have no solution, the lines represented by the equations must be parallel but not coincident. This happens when:
1) The slopes of the two lines are equal.
2) The y-intercepts of the two lines are different.
We will find the slopes of both equations and set them equal to determine r, ensuring the intercepts differ.
Step 3: Write both equations in slope-intercept form
Equation 1: 6x − 14y = 3
Rearrange into slope-intercept form (y = mx + b):
1) Subtract 6x from both sides: −14y = −6x + 3.
2) Divide through by −14:

Final Answer: A) -28.
Did you try all the features and get comfortable using them? You should work on using the Desmos calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must attempt as many questions as you can before the final test. This is the 3rd Practice Test of SAT Math Module 2nd.
Either you can take the 4th Practice Test of SAT Math or the 4th Practice Test of SAT Reading and Writing Module 2nd.
- SAT Test 4th (Math Module 2nd)
- SAT Test 3rd (Math Module 1st)
- SAT Test 4th (Reading and Writing Module 2nd)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


