
Prepare For The SATs: Math Test Module 2nd with Simple Explanations, Tips and Tricks
Have you taken the module 1st? If yes, then you are in the right place. This is the 4th Test of Module 2nd. We have designed a similar exam format with all the necessary features for you to become a master in Math. You take the SAT Test Module Second to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 2nd.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 2ND
The second module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 2nd are only difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 2nd. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH STUDY GUIDE AND PROBLEM SOLUTIONS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: A bus is traveling at a constant speed along a straight portion of road. The equation d = 30t gives the distance d, in feet from a road marker, that the bus will be t seconds after passing the marker. How many feet from the marker will the bus be 2 seconds after passing the marker?
A) 30
B) 32
C) 60
D) 90
Choice C is correct. It’s given that t represents the number of seconds after the bus passes the marker. Substituting 2 for t in the given equation d = 30t yields d = 30(2), or d = 60. Therefore, the bus will be 60 feet from the marker 2 seconds after passing it.
Choice A is incorrect. This is the distance, in feet, the bus will be from the marker 1 second, not 2 seconds, after passing it.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the distance, in feet, the bus will be from the marker 3 seconds, not 2 seconds, after passing it.
Problem Overview
We are given the equation:
d = 30t
where:
~ d represents the distance (in feet) from a road marker,
~ t represents the time (in seconds) after the bus passes the marker.
We are tasked with finding the distance d when t = 2 seconds.
Step 1: Understand the relationship
The equation d = 30t describes a linear relationship between distance and time. The coefficient 30 is the rate of change, or the speed of the bus, in feet per second. This means the bus travels 30 feet every second.
Thus:
~ When t = 1, d = 30(1) = 30 feet.
~ When t = 2, d = 30(2), which we’ll calculate next.
Step 2: Solve for d when t = 2
Substitute t = 2 into the equation:
d = 30t
d = 30(2)
d = 60
So, the bus will be 60 feet from the marker 2 seconds after passing it.
Step 3: Verify the calculation
To verify, consider the bus’s constant speed:
~ In 1 second, the bus travels 30 feet.
~ In 2 seconds, the bus travels 30 + 30 = 60 feet.
This confirms the calculation is correct: d = 60.
Final Answer: C) 60.
2nd Question
Question: Which expression is equivalent to 20w − (4w + 3w)?
A) 10w
B) 13w
C) 19w
D) 21w
Choice B is correct. Combining like terms inside the parentheses of the given expression, 20w – (4w + 3w), yields 20w – (7w). Combining like terms in this resulting expression yields 13w.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the expression
The given expression contains the variable w and involves subtraction as well as grouping with parentheses. Here’s what the components mean:
~ 20w: This is the first term, representing 20 × w.
~ (4w + 3w): This is the second term inside parentheses, which means we need to first combine the terms within the parentheses before subtracting.
Step 2: Simplify the parentheses
Inside the parentheses, add the two terms 4w and 3w. Since both terms have the same variable (w), you can combine them:
4w + 3w = 7w
The expression now becomes:
20w − 7w
Step 3: Simplify the subtraction
Next, subtract 7w from 20w. Since the terms both involve www, you subtract their coefficients:
20w − 7w = (20 − 7)w =13w
So, the simplified expression is: 13w
Step 4: Verify the solution
To verify:
1) Simplify (4w + 3w) to 7w, which is correct.
2) Subtract 7w from 20w, resulting in 13w, which is consistent.
Final Answer: B) 13w.
3rd Question
Question: If 6 + x = 9, what is the value of 18 + 3x?
A) 17
B) 27
C) 37
D) 47
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 27. Multiplying both sides of the given equation by 3 yields 3(6 + x) = 3(9), or 18 + 3x = 27. Therefore, the value of 18 + 3x is 27.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Overview
We are solving the equation 6 + x = 9 to determine the value of x, and then using the result to calculate the value of 18 + 3x.
Step 1: Solve for x in the equation 6 + x = 9
To isolate x:
1) Subtract 6 from both sides of the equation:
6 + x − 6 = 9 − 6
x = 3
Thus, x = 3.
Step 2: Substitute x = 3 into 18 + 3x
Now substitute x = 3 into the second expression 18 + 3x:
18 + 3x = 18 + 3(3)
Step 3: Simplify 18 + 3(3)
1) Multiply 3 and 3:
3(3) = 9
2) Add 18 + 9:
18 + 9 = 27
Thus, the value of 18 + 3x is: 27.
Step 4: Verify the Solution
1) Check that 6 + x = 9 gives x = 3. Substituting x = 3 confirms 6 + 3 = 9, which is correct.
2) Substituting x = 3 into 18 + 3x gives 27, confirming the result.
Final Answer: B) 27.
4th Question
y = x2 − 14x + 22
Question: The given equation relates the variables x and y. For what value of x does the value of y reach its minimum?
A) 4
B) 7
C) 14
D) 22
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 7. When an equation is of the form y = ax2 + bx + c, where a, b, and c are constants, the value of y reaches its minimum when x = –b/2a. Since the given equation is of the form y = ax2 + bx + c, it follows that a = 1, b = -14, and c = 22. Therefore, the value of y reaches its minimum when x = (-14)/2(1), or x = 7.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Overview
The given equation is:
y = x2 − 14x + 22
This is a quadratic equation in standard form y = ax2 + bx + c. Since the coefficient of x2 (i.e., a = 1) is positive, the parabola opens upwards, meaning it has a minimum value at its vertex.
We are tasked to find the x-coordinate of the vertex, where y reaches its minimum.
Step 1: Use the Vertex Formula
The x-coordinate of the vertex of a parabola described by y = ax2 + bx + c is given by the formula:
x = −b/2a
Here:
~ a = 1 (the coefficient of x2)
~ b = −14 (the coefficient of x)
Substitute these values into the formula:
x = −14/2(1)
x = 14/2
x = 7
Thus, the x-coordinate of the vertex is x = 7.
Step 2: Verify the Solution
To confirm that y reaches its minimum at x = 7, observe that:
1) The parabola opens upwards because a = 1 > 0, which means the vertex represents a minimum point.
2) At x = 7, y is indeed at its lowest value.
Final Answer: B) 7.
5th Question
Question: Which expression is equivalent to 12y2 + 8y?
A) y(12y + 8)
B) 8y(12y + 1)
C) 12y(y + 8)
D) y2(12y + 8)
Choice A is correct.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Analyze the Problem
The given expression is 12y2 + 8y. To simplify it into factored form, identify and factor out the greatest common factor (GCF) of the terms.
The two terms in the expression are:
~ 12y: This term consists of 12 and y2.
~ 8y: This term consists of 8 and y.
The GCF of 12y2 and 8y is:
~ The GCF of 12 and 8 is 4.
~ The smallest power of y in the terms is y.
Thus, the GCF of 12y2 and 8y is 4y.
Step 2: Factor the Expression
Factor out 4y from both terms:
12y2 + 8y = 4y(3y + 2)
Step 3: Verify the Factored Expression
Expand 4y(3y + 2) to ensure it equals the original expression:
4y(3y) + 4y(2) = 12y2 + 8y
This confirms that 4y(3y + 2) is equivalent to 12y2 + 8y.
Final Answer: A) y(12y + 8).
6th Question
Question: The function f is defined by f(x) = 1/10 x − 2. What is the y-intercept of the graph of y = f(x) in the xy-plane?
A) (−2, 0)
B) (0, −2)
C) (0, 1/10)
D) (1/10, 0)
Choice B is correct. The y-intercept of the graph of a function in the xy-plane is the point on the graph where x =0. It′s given that f(x) = 1x/10 – 2. Substituting 0 for x in this equation yields f(0) = 1(0)/10 – 2, or f(0) = -2. Since it′s given that y = f(x), it follows that y = -2 when x = 0. Therefore, the y-intercept of the graph of y = f(x) in the xy-plane is (0, -2).
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
The Role of the y-Intercept
The y-intercept is the point where the graph crosses the y-axis. By definition, any point on the y-axis has an x-coordinate of 0, because the y-axis represents the line where x = 0 across the entire xy-plane.
For example:
~ A point like (0, 3) lies on the y-axis because its x-coordinate is 0.
~ Similarly, (0, −5) is also on the y-axis.
Why x = 0 for the y-Intercept
When finding the y-intercept, we are asking: What is the value of y when x is 0? This is because the y-intercept is specifically the point of intersection with the y-axis, and along the y-axis, the x-coordinate is always zero.

Final Answer: B) (0, -2).
7th Question
Question: The function f is defined by f(x) = 7x3. In the xy-plane, the graph of y = g(x) is the result of shifting the graph of y = f(x) down 2 units. Which equation defines function g?
A) g(x) = 7/2 x3
B) g(x) = 7x3/2
C) g(x) = 7x3 + 2
D) g(x) = 7x3 − 2
Choice D is correct. If the graph of y = g(x) is the result of shifting the graph of y = f(x) down k units in the xy-plane, the function g can be defined by an equation of the form g(x) = f(x) – k. It’s given that f(x) = 7x3 and the graph of y = g(x) is the result of shifting the graph of y = f(x) down 2 units. Substituting 7x3 for f(x) and 2 for k in the equation g(x) = f(x) – k yields g(x) = 7x3 – 2.
Choice A is incorrect and may result from conceptual errors.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect. This equation defines a function g for which the graph of y = g(x) is the result of shifting the graph of y = f(x) up, not down, 2 units.
Understanding the Problem
The function f(x) = 7x3 is a cubic function. The graph of y = g(x) is obtained by shifting the graph of y = f(x) down by 2 units. We need to determine the equation for g(x), given this transformation.
Key Concept: Vertical Shifting
When a graph is shifted vertically:
~ If the graph is shifted up, we add the shift amount to the function: g(x) = f(x) + amount.
~ If the graph is shifted down, we subtract the shift amount from the function: g(x) = f(x) − amount.
Since the graph is shifted down by 2 units, the new function becomes:
g(x) = f(x) − 2
Substituting f(x)
We are given f(x) = 7x3. Substituting this into g(x):
g(x) = 7x3 − 2
Thus, the equation for g(x) is:
g(x) = 7x3 − 2
Verifying the Answer
Let’s analyze each answer choice:
Option A) g(x) = 7/2 x3: This divides 7x3, which does not correspond to a vertical shift. Incorrect.
Option B) g(x) = 7x3/2: This changes the power of x, which does not represent a vertical shift. Incorrect.
Option C) g(x) = 7x3 + 2: This represents shifting the graph up by 2 units, not down. Incorrect.
Option D) g(x) = 7x3 − 2: This correctly represents shifting the graph down by 2 units. Correct.
Final Answer: D) g(x) = 7x3 − 2.
8th Question
x + 7 = 10
(x + 7)2 = y
Question: Which ordered pair (x, y) is a solution to the given system of equations?
A) (3, 100)
B) (3, 3)
C) (3, 10)
D) (3, 70)
Choice A is correct. The solution to a system of equations is the ordered pair (x, y) that satisfies all equations in the system. It’s given by the first equation in the system that x + 7 = 10. Substituting 10 for x + 7 into the second equation yields 102 = y, or y = 100. The x-coordinate of the solution to the system of equations can be found by subtracting 7 from both sides of the equation x + 7 = 10, which yields x = 3. Therefore, the ordered pair (3, 100) is a solution to the given system of equations.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Solve the First Equation
The first equation is:
x + 7 = 10
Subtract 7 from both sides to isolate x:
x = 10 − 7
x = 3
Now, we know x = 3.
Step 2: Substitute x into the Second Equation
The second equation is:
(x + 7)2 = y
~ Substitute x = 3 into the equation:
(3 + 7)2 = y
~ Simplify the expression inside the parentheses:
102 = y
Simplify further:
y = 100
Step 3: Verify the Solution
The solution is (x, y) = (3, 100). Let’s verify this by substituting x = 3 and y = 100 into both equations:
1) For the first equation:
x + 7 = 10 becomes 3 + 7 = 10
This is true.
2) For the second equation:
(x + 7)2 = y becomes (3 + 7)2 = 100
102 = 100
This is also true.
Since both equations are satisfied, (3, 100) is indeed the solution.
Final Answer: A) (0, 100).
9th Question
Question: Which expression is equivalent to (7x3 + 7x) − (6x3 − 3x)?
A) x3 + 10x
B) −13x3 + 10x
C) −13x3 + 4x
D) x3 + 4x
Choice A is correct. Applying the distributive property, the given expression can be written as 7x3 + 7x – 6x3 + 3x. Grouping like terms in this expression yields (7x3 – 6x3) + (7x + 3x). Combining like terms in this expression yields x3 +10x.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis
We need to simplify the expression:(
(7x3 + 7x) − (6x3 − 3x)
The goal is to distribute, combine like terms, and determine which option matches the simplified expression.
Step-by-Step Solution
Step 1: Remove the Parentheses
We start by rewriting the expression without parentheses, distributing the negative sign in the second group:
(7x3 + 7x) − (6x3 − 3x)
Distribute the negative sign:
7x3 + 7x − 6x3 + 3x
Step 2: Combine Like Terms
Now, group like terms for x3 and x:
~ x3-terms: 7x3 − 6x3 = x3
~ x-terms: 7x + 3x = 10x
So, the simplified expression becomes:
x3 + 10x
Final Answer: A) x3 + 10x.
10th Question
Question: The function p is defined by p(n) = 7n3. What is the value of n when p(n) is equal to 56?
A) 2
B) 8/3
C) 7
D) 8
Choice A is correct. It’s given that p(n) = 7n3. Substituting 56 for p(n) in this equation yields 56 = 7n3. Dividing each side of this equation by 7 yields 8 = n3. Taking the cube root of each side of this equation yields 2 = n. Therefore, when p(n) is equal to 56, the value of n is 2.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis
The function p(n) is defined as:
p(n) = 7n3
We are tasked to find the value of nnn such that p(n) = 56. This involves solving the equation:
7n3 = 56
Step-by-Step Solution
Step 1: Write the Equation
Start by substituting p(n) = 56 into the function:
7n3 = 56
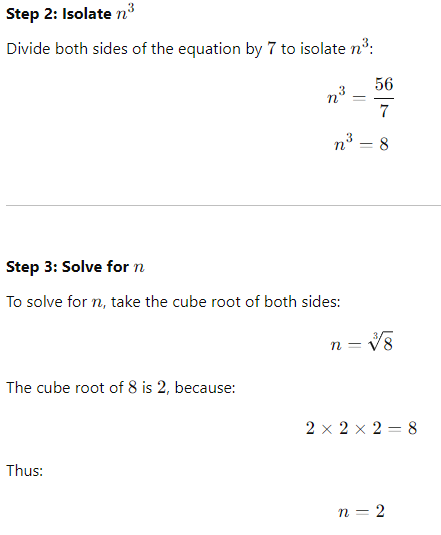
Verification
Substitute n = 2 back into the original function to verify:
p(n) = 7n3
p(2) = 7(23)
= 7 × 8 = 56
This confirms that the solution is correct.
Final Answer: A) 2.
11th Question
Question: Line p is defined by 2y + 18x = 9. Line r is perpendicular to line pin the xy-plane. What is the slope of line r?
A) −9
B) −1/9
C) 1/9
D) 9
Choice C is correct. It’s given that line r is perpendicular to line p in the xy-plane. This means that the slope of line r is the negative reciprocal of the slope of line p. If the equation for line p is rewritten in slope-intercept form y = mx + b, where m and b are constants, then m is the slope of the line and (0, b) is its y-intercept. Subtracting 18x from both sides of the equation 2y + 18x = 9 yields 2y = -18x + 9. Dividing both sides of this equation by 2 yields y = -9x + 9/2. It follows that the slope of line p is -9. The negative reciprocal of a number is -1 divided by the number. Therefore, the negative reciprocal of -9 is -1/-9, or 1/9. Thus, the slope of line r is 1/9.
Choice A is incorrect. This is the slope of line p, not line r.
Choice B is incorrect. This is the reciprocal, not the negative reciprocal, of the slope of line p.
Choice D is incorrect. This is the negative, not the negative reciprocal, of the slope of line p.
Problem Analysis
We are tasked with finding the slope of a line r that is perpendicular to a given line p, whose equation is:
2y + 18x = 9
The key here is that the slopes of perpendicular lines are negative reciprocals of each other.
Step-by-Step Solution
Step 1: Rewrite Line p in Slope-Intercept Form
The slope-intercept form of a line is:
y = mx + b
where m is the slope and b is the y-intercept.
Start with the equation of line p:
2y + 18x = 9
Isolate y by first subtracting 18x from both sides:
2y = −18x + 9
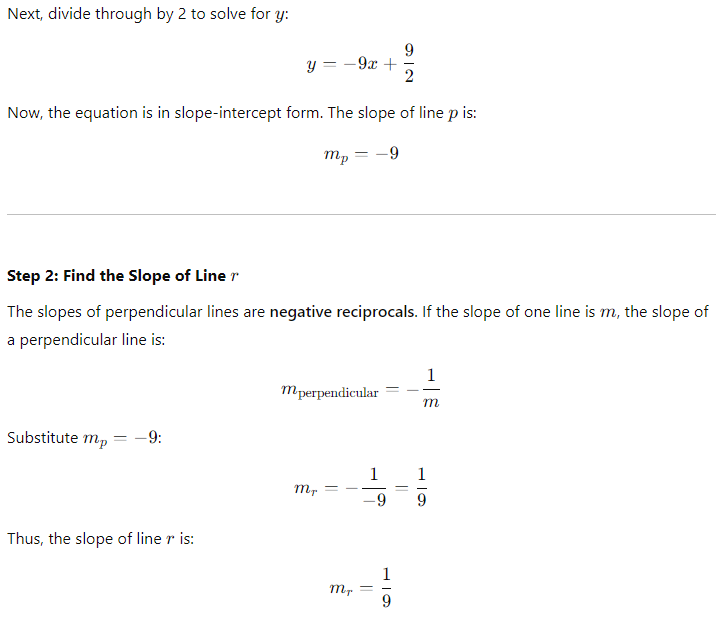
Verification
To verify, check the product of the slopes of perpendicular lines. For perpendicular lines, the product of their slopes is:
mp ⋅ mr = −1
Substitute mp = −9 and mr = 1/9:
(−9) ⋅ (1/9) = −1
This confirms the slopes are indeed perpendicular.
Final Answer: C) 1/9.
12th Question
f(t) = 8,000(0.65)t
Question: The given function f models the number of coupons a company sent to their customers at the end of each year, where t represents the number of years since the end of 1998, and 0 ≤ t ≤ 5. If y = f(t) is graphed in the t y-plane, which of the following is the best interpretation of the y-intercept of the graph in this context?
A) The minimum estimated number of coupons the company sent to their customers during the 5 years was 1,428.
B) The minimum estimated number of coupons the company sent to their customers during the 5 years was 8,000.
C) The estimated number of coupons the company sent to their customers at the end of 1998 was 1,428.
D) The estimated number of coupons the company sent to their customers at the end of 1998 was 8,000.
Choice D is correct. The y-intercept of a graph in the ty-plane is the point where t = 0. For the given function f, the y-intercept of the graph of y = f(t) in the ty-plane can be found by substituting 0 for t in the equation y = 8,000(0.65)t, which gives y = 8,000(0.65)0. This is equivalent to y = 8,000(1), or y = 8,000. Therefore, the y-intercept of the graph of y = f(t) is (0, 8000). It’s given that the function f models the number of coupons a company sent to their customers at the end of each year. Therefore, f(t) represents the estimated number of coupons the company sent to their customers at the end of each year. It’s also given that t represents the number of years since the end of 1998. Therefore, t = 0 represents 0 years since the end of 1998, or the end of 1998. Thus, the best interpretation of the y-intercept of the graph of y = f(t) is that the estimated number of coupons the company sent to their customers at the end of 1998 was 8,000.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Analysis
We are tasked with interpreting the y-intercept of the graph of the function f(t) = 8,000(0.65)t, which models the number of coupons sent by a company to customers. The variable t represents the number of years since the end of 1998, and f(t) represents the number of coupons sent at the end of year t.
The y-intercept corresponds to the value of f(t) when t = 0. This represents the starting value of the function.
Step-by-Step Solution
Step 1: Calculate the y-Intercept
The y-intercept of the function is the value of f(t) when t = 0:
f(0) = 8,000(0.65)0
Using the property x0 = 1 for any non-zero x, we have:
f(0) = 8,000 ⋅ 1 = 8,000
Thus, the y-intercept is:
(0, 8000)
Step 2: Interpret the y-Intercept
The y-intercept occurs when t = 0, which corresponds to the end of 1998 (since t is the number of years after 1998). Therefore:
f(0) = 8,000
means that at the end of 1998, the company sent 8,000 coupons to their customers.
Explanation of Context
The y-intercept represents the initial number of coupons sent at the start of the modeled period. This is the baseline number from which the company began reducing the number of coupons sent over time (as indicated by the factor 0.65, which reduces the number of coupons by 35% each year).
Final Answer: D) The estimated number of coupons the company sent to their customers at the end of 1998 was 8,000.
13th Question
Question: Triangle XYZ is similar to triangle RST such that X, Y, and Z correspond to R, S, and T, respectively. The measure of ∠Z is 20° and 2XY = RS. What is the measure of ∠T?
A) 2°
B) 10°
C) 20°
D) 40°
Choice C is correct. It’s given that triangle XYZ is similar to triangle RST, such that X, Y, and Z correspond to R, S, and T, respectively. Since corresponding angles of similar triangles are congruent, it follows that the measure of ∠Z is congruent to the measure of ∠T. It’s given that the measure of ∠Z is 20°. Therefore, the measure of ∠T is 20°.
Choice A is incorrect and may result from a conceptual error.
Choice B is incorrect. This is half the measure of ∠Z.
Choice D is incorrect. This is twice the measure of ∠Z.
Problem Breakdown:
We are tasked with finding the measure of ∠T in triangle RST, which is similar to triangle XYZ.
Step 1: Understanding Similar Triangles
~ In similar triangles, corresponding angles are equal, and the ratios of corresponding sides are proportional.
~ X corresponds to R, Y to S, and Z to T. This means: ∠Z = ∠T.
Step 2: Using the Given Information
~ ∠Z = 20∘.
~ Since ∠Z corresponds to ∠T, the measure of ∠T is also 20∘.
Step 3: Verifying the Relationships
Even though we are given a proportional relationship (2XY = RS), this affects the side lengths and not the angles. Therefore, we can directly equate the corresponding angles.
Final Answer: ∠T = 20∘.
14th Question
y = 4x
3x + y = 18
Question: The solution to the given system of equations is (x, y). What is the value of 7x?
A) 42
B) 35
C) 28
D) 7
Choice A is correct.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Analyze the Problem
We are solving a system of linear equations with two variables:
1) y = 4x
2) 3x + y = 18
The goal is to find the value of 7x.
Step 2: Substitute y = 4x into the Second Equation
Substitute y = 4x into the equation 3x + y = 18:
3x + 4x = 18
Step 3: Find the Value of 7x
From the equation 7x = 18, we see that 7x is already given as 18.
Final Answer: A) 42.
15th Question
Question: A cube has an edge length of 56 inches. What is the volume, in cubic inches, of the cube?
A) 336
B) 3,136
C) 17,576
D) 175,616
Choice B is correct.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Analyze the Problem
The volume of a cube is calculated using the formula:
V = edge length
Here, the edge length is given as 56 inches. Substituting this value into the formula will give the volume of the cube.
Step 2: Substitute and Solve
The formula for the volume is:
V = 563
First, calculate 563:
563 = 56 × 56 × 56
Step-by-step:
1) 56 × 56 = 3,136
2) 3,136 × 56 = 175,616
So, the volume of the cube is:
V = 175,616 cubic inches
Final Answer: D) 175,616.
16th Question
Question: The minimum value of y is 8 less than 4 times another number m. Which inequality shows the possible values of y?
A) y ≤ 4m − 8
B) y ≥ 4m − 8
C) y ≤ 8 − 4m
D) y ≥ 8 − 4m
Choice B is correct.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Analyze the Problem
We are tasked with expressing a relationship between two variables, y and m, as an inequality. The problem states that the minimum value of y is 8 less than 4 times m. This means y can take values greater than or equal to 4m − 8, as it is at least 4m − 8.
Step 2: Translate into a Mathematical Inequality
The phrase “minimum value of y is 8 less than 4 times m“ can be written mathematically as:
y ≥ 4m − 8
Here:
~ 4m − 8: Represents the minimum value.
~ y ≥: Represents that y is at least this minimum value.
Step 3: Select the Correct Option
From the given options:
B) y ≥ 4m − 8
This matches our inequality.
Final Answer: B) y > 4m – 8.
17th Question
Question: Two variables, a and b, are related such that for each increase of 1 in the value of a, the value of b increases by a factor of 3. When a = 0, b = 150. Which equation represents this relationship?
A) b = 3(a)150
B) b = 3(150)a
C) b = 150(a)3
D) b = 150(3)a
Choice D is correct.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
Step 1: Understand the relationship
~ When a = 0, b = 150. This is the initial condition.
~ For each increase of 1 in a, b increases by a factor of 3. This indicates exponential growth.
The general equation for exponential growth is:
b = b0 ⋅ ra
Where:
~ b0 is the initial value when a = 0.
~ r is the growth factor for each unit increase in a.
Step 2: Substitute the given values
~ Initial value: b0 = 150.
~ Growth factor: r = 3.
The equation becomes:
b = 150 ⋅ 3a
Step 3: Match the equation to the choices
The correct equation matches option D:
b = 150(3)a
Verification
1) Test with a = 0:
b = 150 ⋅ 30 = 150 ⋅ 1 = 150
Correct.
2) Test with a = 1:
b = 150 ⋅ 31 = 150 ⋅ 3 = 450
Correct.
3) Test with a = 2:
b = 150 ⋅ 32 = 150 ⋅ 9 = 1350
Correct.
Final Answer: D) b = 150(3)a
18th Question
Question: Rectangles PQRST and UVWXY are similar. The length of each side of UVWXY is 5 times the length of the corresponding side of PQRST. The area of PQRST is 48 square units. What is the area, in square units, of UVWXY?
A) 240
B) 480
C) 1,200
D) 1,920
Choice C is correct.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand Similar Rectangles:
When two rectangles are similar, the ratio of their side lengths is constant. If the ratio of the side lengths is k, then the ratio of their areas is k2.
Step 2: Given Information:
~ The ratio of the side lengths of UVWXY to PQRST is 5 : 1.
~ The area of PQRST is 48 square units.
Step 3: Calculate the Area Ratio:
The area ratio between the rectangles is the square of the side length ratio:
Area ratio = k2 = 52 = 25
Step 4: Find the Area of UVWXY:
Multiply the area of PQRST by the area ratio to find the area of UVWXY:
Area of UVWXY = Area of PQRST × Area ratio = 48 × 25 = 1,200 square units.
Answer:
The area of UVWXY is 1,200 square units (Choice C).
Explanation of the Approach:
~ Why Use Area Ratio?
For similar figures, the scale of the areas by the square of the side length ratio makes it faster to calculate the larger area without computing individual dimensions.
~ Why k2?
Area is a two-dimensional measure, so both dimensions (length and width) are scaled by the same factor, k. The total scaling effect is k × k = k2.
Final Answer: C) 1,200.
19th Question

Question: Which of the following statements must be true?
I. The median of data set A is equal to the median of data set B.
II. The standard deviation of data set A is equal to the standard deviation of data set B.
A) I only
B) II only
C) I and II
D) Neither I nor II
Choice A is correct. The median of a data set with an odd number of values that are in ascending or descending order is the middle value of the data set. Since the distribution of the values of both data set A and data set B form symmetric dot plots, and each data set has an odd number of values, it follows that the median is given by the middle value in each of the dot plots. Thus, the median of data set A is 13, and the median of data set B is 13. Therefore, statement I is true. Data set A and data set B have the same frequency for each of the values 11, 12, 14, and 15. Data set A has a frequency of 1 for values 10 and 16, whereas data set B has a frequency of 2 for values 10 and 16. Standard deviation is a measure of the spread of a data set; it is larger when there are more values further from the mean, and smaller when there are more values closer to the mean. Since both distributions are symmetric with an odd number of values, the mean of each data set is equal to its median. Thus, each data set has a mean of 13. Since more of the values in data set A are closer to 13 than data set B, it follows that data set A has a smaller standard deviation than data set B. Thus, statement II is false. Therefore, only statement I must be true.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
We are tasked with analyzing the dot plots of Data Set A and Data Set B and determining whether the following statements are true:
1) The median of data set A is equal to the median of data set B.
2) The standard deviation of data set A is equal to the standard deviation of data set B.
Step 1: Understanding the Median
The median is the middle value in a sorted data set.
~ Data Set A and Data Set B both have 15 data points each.
~ The median is the 8th value when the data points are arranged in order.
Data Set A:
Values: 10, 11, 11, 12, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 16
Median = 14
Data Set B:
Values: 10, 11, 11, 12, 12, 12, 13, 14, 14, 14, 15, 15, 16, 16, 16
Median = 14
Since both medians are equal, Statement I is true.
Step 2: Understanding Standard Deviation
The standard deviation measures how spread out the values in a data set are from the mean.
Data Set A:
Values: 10, 11, 11, 12, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 16
Data Set B:
Values: 10, 11, 11, 12, 12, 12, 13, 14, 14, 14, 15, 15, 16, 16, 16
Observation of Variability:
~ Both data sets have the same range (10 to 16).
~ However, the frequencies of the individual values differ. In Data Set A, values like 15 and 16 occur more frequently than in Data Set B, while 12 occurs more frequently in Data Set B.
Since the distributions are not identical, the spreads of the data differ, and hence, the standard deviations are not equal.
Statement II is false.
Step 3: Conclusion
I. Statement I is true.
II. Statement II is false.
Final Answer: A) I only.
20th Question
Question:

Choice B is correct.


Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect. This is the length, in inches, of the hypotenuse.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:

Let’s find the value for a.
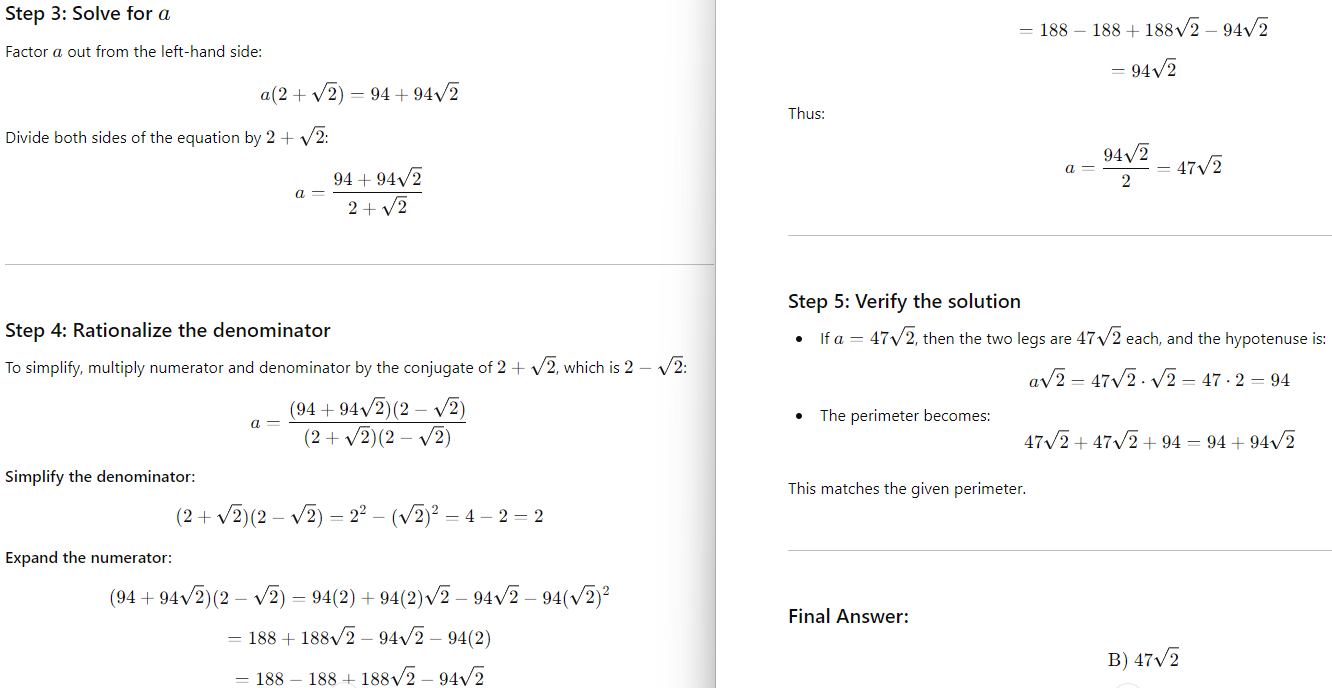
Final Answer: Option B.
21th Question
-9x2 + 30x + c = 0
Question: In the given equation, c is a constant. The equation has exactly one solution. What is the value of c?
A) 3
B) 0
C) −25
D) −53
Choice C is correct. It’s given that the equation -9x2 + 30x + c = 0 has exactly one solution. A quadratic equation of the form ax2 + bx + c = 0 has exactly one solution if and only if its discriminant, -4ac + b2, is equal to zero. It follows that for the given equation, a = -9 and b = 30. Substituting -9 for a and 30 for b into b2 – 4ac yields 302 – 4(-9)(c), or 900 + 36c. Since the discriminant must equal zero, 900 + 36c = 0. Subtracting 36c from both sides of this equation yields 900 = -36c. Dividing each side of this equation by -36 yields -25 = c. Therefore, the value of c is -25.
Choice A is incorrect. If the value of c is 3, this would yield a discriminant that is greater than zero. Therefore, the given equation would have two solutions, rather than exactly one solution.
Choice B is incorrect. If the value of c is 0, this would yield a discriminant that is greater than zero. Therefore, the given equation would have two solutions, rather than exactly one solution.
Choice D is incorrect. If the value of c is -53, this would yield a discriminant that is less than zero. Therefore, the given equation would have no real solutions, rather than exactly one solution.
Step-by-Step Solution:
The given quadratic equation is:
−9x2 + 30x + c = 0
We are tasked to find the value of c such that the equation has exactly one solution.
Step 1: Condition for a Quadratic Equation to Have One Solution
A quadratic equation has exactly one solution when the discriminant is zero. The discriminant (Δ) for a quadratic equation ax2 + bx + c = 0 is given by:
Δ = b2 − 4ac
If Δ = 0, the equation has one solution because the vertex of the parabola touches the x-axis (the roots coincide).
Step 2: Identify a, b, and c
In the given equation:
−9x2 + 30x + c = 0
~ a = −9
~ b = 30
~ c = c (a constant we need to find)
Step 3: Use the Discriminant Formula
Substitute a = −9, b = 30, and c = c into the discriminant formula:
Δ = b2 − 4ac
Δ = (30)2 − 4(−9)(c)
Δ = 900 − (−36c)
Δ = 900 + 36c
Step 4: Set the Discriminant Equal to Zero
For the quadratic equation to have one solution, Δ = 0:
900 + 36c = 0
Solve for c:
36c = −900
c = −900/36
c = −25
Step 5: Verify the Result
Substitute c = −25 back into the discriminant formula to confirm:
Δ = 900 + 36(−25)
Δ = 900 − 900
Δ = 0
The discriminant is zero, so the equation has exactly one solution. This confirms that c = −25 is correct.
Final Answer: C) −25.
22th Question
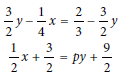
Question: In the given system of equations, p is a constant. If the system has no solution, what is the value of p?
A) 6
B) -6
C) 18
D) -18
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A: The correct answer is 6. A system of two linear equations in two variables, x and y, has no solution if the lines represented by the equations in the xy-plane are parallel and distinct. Lines represented by equations in standard form, Ax + By = C and Dx + Ey = F, are parallel if the coefficients for x and y in one equation are proportional to the corresponding coefficients in the other equation, meaning D/A = E/B; and the lines are distinct if the constants are not proportional, meaning F/C is not equal to D/A or E/B. The first equation in the given system is 3/2 y – 1/4 x = 2/3 – 3/2 y. Multiplying each side of this equation by 12 yields 18y – 3x = 8 – 18y. Adding 18y to each side of this equation yields 36y – 3x = 8, or -3x + 36y = 8. The second equation in the given system is 1/2 x + 3/2 = py + 9/2. Multiplying each side of this equation by 2 yields x + 3 = 2py + 9. Subtracting 2py from each side of this equation yields x + 3 – 2py = 9. Subtracting 3 from each side of this equation yields x – 2py = 6. Therefore, the two equations in the given system, written in standard form, are -3x + 36y = 8 and x – 2py = 6. As previously stated, if this system has no solution, the lines represented by the equations in the xy-plane are parallel and distinct, meaning the proportion 1/-3 = -2p/36, or -1/3 = –p/18, is true and the proportion 6/8 = 1/-3 is not true. The proportion 6/8 = 1/-3 is not true. Multiplying each side of the true proportion, -1/3 = –p/18, by -18 yields 6 = p. Therefore, if the system has no solution, then the value of p is 6.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
We are tasked to find the value of p such that the system has no solution. For a system of linear equations to have no solution, their slopes must be equal (i.e., the lines are parallel), but the equations must represent different lines (they do not intersect).

Now, let’s compare the two equations from Step 1 and Step 2.

Step 4: Solve for p
Cross-multiply to solve:
2p = 12
p = 12/2
p = 6
Step 5: Verify the solution
For p = 6:
~ The slopes of the two equations are equal, making the lines parallel.
~ Since the lines are parallel, they have no intersection, confirming that the system has no solution.
Final Answer: A) 6.
Did you try all the features and get comfortable using them? You should work on using the Desmos calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must attempt as many questions as you can before the final test. This is the 4th Practice Test of SAT Math Module 2nd.
Either you can take the 5th Practice Test of SAT Math or the 5th Practice Test of SAT Reading and Writing Module 2nd.
- SAT Test 5th (Math Module 2nd)
- SAT Test 4th (Math Module 1st)
- SAT Test 5th (Reading and Writing Module 2nd)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


