
Prepare for the SAT: Math Test Module 1st with Simple Step-by-step Solutions
Hey, not only you will take the SAT Test but also you will learn all Math problems by understanding step-by-step solutions. This is the 5th version for you to practice your SAT Math learning. Like the other exams, it has the same format and all the necessary features for you to become a master in math. You just take the SAT Test Module First to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after step-by-step explanations.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each split into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 1st.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 1ST
The first module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 1st are from easy to difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 1st. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH TEST SOLUTIONS WITH STEP-BY-STEP EXPLANATION
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
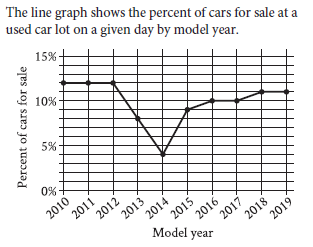
Question: For what model year is the percent of cars for sale the smallest?
A) 2012
B) 2013
C) 2014
D) 2015
Choice C is correct. For the given line graph, the percent of cars for sale at a used car lot on a given day is represented on the vertical axis. The percent of cars for sale is the smallest when the height of the line graph is the lowest. The lowest height of the line graph occurs for cars with a model year of 2014.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis:
The line graph shows the percentage of cars for sale at a used car lot for various model years (2010 to 2019). The question asks us to determine the model year corresponding to the smallest percentage of cars for sale.
Step-by-Step Solution:
Step 1: Understand the graph
~ The x-axis represents the model year (2010 to 2019).
~ The y-axis represents the percentage of cars for sale (from 0% to 15%).
Each point on the graph represents the percentage of cars for sale for the corresponding model year.
Step 2: Identify the smallest percentage
~ From the graph, visually inspect the lowest point of the line.
~ The lowest percentage occurs around 5%.
~ This lowest point corresponds to the model year 2014.
Step 3: Verify the solution
To ensure the correct interpretation:
~ The percentages are highest around 10-15% for other model years.
~ The line dips significantly for 2014, indicating the smallest percentage of cars for sale.
Final Answer:
The model year with the smallest percentage of cars for sale is: 2014
2nd Question
Question: For a particular machine that produces beads, 29 out of every 100 beads it produces have a defect. A bead produced by the machine will be selected at random. What is the probability of selecting a bead that has a defect?
A) 1/2,900
B) 1/29
C) 29/100
D) 29/10
Choice C is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Question Breakdown:
The question asks us to find the probability of selecting a defective bead produced by a machine. For every 100 beads produced, 29 are defective.

Final Answer: C) 29/100.
3rd Question
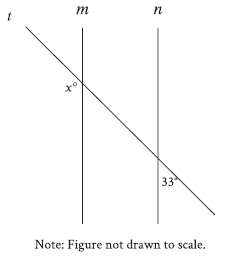
Question: In the figure, line m is parallel to line n, and line t intersects both lines. What is the value of x?
A) 33
B) 57
C) 123
D) 147
Choice D is correct. It’s given that line m is parallel to line n, and line t intersects both lines. It follows that line t is a transversal. When two lines are parallel and intersected by a transversal, exterior angles on the same side of the transversal are supplementary. Thus, x + 33 = 180. Subtracting 33 from both sides of this equation yields x = 147. Therefore, the value of x is 147.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Evaluation:
Step 1: Analyze the given information
~ Lines m and n are parallel.
~ Line t is a transversal that intersects both m and n.
~ An angle of 33∘ is formed at the intersection of line t with line n.
~ The angle x∘ is formed at the intersection of line t with line m.
We aim to find the value of x, considering the relationship between the angles formed by transversal and parallel lines.
Step 2: Understand angle relationships
1. Interior and exterior angles: When a transversal intersects parallel lines:
~ Same-side interior angles are supplementary (they add up to 180∘).
~ Corresponding angles are congruent.
2. The 33∘ angle is an interior angle on the lower side of t, relative to line n.
~ The angle x∘, on the upper side of t relative to line m, is its same-side interior angle.
Step 3: Use the same-side interior angle property
For same-side interior angles formed by a transversal with parallel lines:
x + 33 = 180
Step 4: Solve for x
x = 180 − 33
x = 147
Final Answer: 147∘
4th Question
Question: Amar deposited a fixed amount into his savings account each month. The function f(t) = 200 + 50t gives the amount, in dollars, in Amar’s savings account after t monthly deposits. What is the best interpretation of 50 in this context?
A) With each monthly deposit, the amount in Amar’s savings account increased by $50.
B) Before Amar made any monthly deposits, the amount in his savings account was $50.
C) After 1 monthly deposit, the amount in Amar’s savings account was $50.
D) Amar made a total of 50 monthly deposits.
Option A is the correct answer.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Analyze the function f(t) = 200 + 50t
The function f(t) describes the total amount in Amar’s savings account after t months. Let’s break it down:
~ Initial amount (200): The constant term (200) represents the amount already in Amar’s account before he starts depositing money.
~ Rate of change (50): The coefficient of t (50) represents the increase in the account balance for each monthly deposit. This is the amount Amar deposits each month.
Step 2: Interpret the meaning of 50
From the structure of the function, 50t means that for every additional month (t), the account balance increases by $50. Thus, 50 represents the amount Amar deposits into his savings account each month.
Step 3: Determine the best answer
The correct answer is: A) With each monthly deposit, the amount in Amar’s savings account increased by $50.
Verification:
Let’s test the function for a couple of values of t:
1. When t = 0: f(0) = 200 + 50(0) = 200
This confirms that the initial amount in the account is $200, before any deposits.
2. When t = 1: f(1) = 200 + 50(1) = 250
After one monthly deposit, the balance increases by $50 to $250.
3. When t = 2: f(2) = 200 + 50(2) = 300
After two monthly deposits, the balance increases by another $50 to $300.
This confirms that 50 is the amount Amar deposits into his savings account each month.
5th Question
Question: A machine produces boxes at a constant rate of 36 boxes per minute. At what rate, in boxes per hour, does the machine produce the boxes?
A) 60
B) 2,160
C) 36
D) 96
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Understand the problem
The machine produces 36 boxes per minute. To calculate the rate in boxes per hour, we need to determine how many minutes are in one hour and then multiply the given rate by that time.
Step 2: Convert minutes to hours
There are 60 minutes in one hour. If the machine produces 36 boxes in 1 minute, in 60 minutes it will produce:
Rate in boxes per hour = 36 × 60
Step 3: Perform the calculation
36 × 60 = 2,160
Thus, the machine produces 2,160 boxes per hour.
Final Answer: The machine produces 2,160 boxes per hour.
6th Question
Data set X: 5, 9, 9, 13
Data set Y: 5, 9, 9, 13, 27
Question: The lists give the values in data sets X and Y. Which statement correctly compares the mean of data set X and the mean of data set Y?
A) The mean of data set X is greater than the mean of data set Y.
B) The mean of data set X is less than the mean of data set Y.
C) The means of data set X and data set Y are equal.
D) There is not enough information to compare the means.
Choice B is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Understand the problem
The problem involves two data sets, X and Y:
~ Data set X = {5, 9, 9, 13}
~ Data set Y = {5, 9, 9, 13, 27}
We need to determine which statement correctly compares the means (average values) of the two data sets.

Step 4: Compare the means
~ The mean of data set X is 9.
~ The mean of data set Y is 12.6.
Since 9 < 12.69, the mean of data set X is less than the mean of data set Y.
Final Answer: B) The mean of data set X is less than the mean of data set Y.
7th Question
Question: A rocket contained 467,000 kilograms (kg) of propellant before launch. Exactly 21 seconds after launch, 362,105 kg of this propellant remained. On average, approximately how much propellant, in kg, did the rocket burn each second after launch?
A) 4,995
B) 17,243
C) 39,481
D) 104,895
Choice A is correct. It’s given that the rocket contained 467,000 kilograms (kg) of propellant before launch and had 362,105 kg remaining exactly 21 seconds after launch. Finding the difference between the amount, in kg, of propellant before launch and the remaining amount, in kg, of propellant after launch gives the amount, in kg, of propellant burned during the 21 seconds: 467,000 – 362,105 = 104,895. Dividing the amount of propellant burned by the number of seconds yields 104,895/21= 4,995. Thus, an average of 4,995 kg of propellant burned each second after launch.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from finding the amount of propellant burned, rather than the amount of propellant burned each second.
Step-by-Step Solution:
Step 1: Understand the problem
We are tasked with calculating the average amount of propellant burned per second by the rocket after launch.
~ Initial amount of propellant: 467,000 kg
~ Remaining amount after 21 seconds: 362,105 kg
~ Time elapsed: 21 seconds
The average rate of propellant burned per second can be calculated using the formula:

Perform the division:
Rate = 4,995 kg/second.
Step 4: Identify the correct answer
The average amount of propellant burned each second is 4,995 kg/second, which corresponds to Option A.
Final Answer: A) 4,995
8th Question
Question: If 4x + 2 = 12, what is the value of 16x + 8?
A) 40
B) 48
C) 56
D) 60
Choice B is correct. Multiplying both sides of the given equation by 4 yields (4)(4x + 2) = (4)(12), or 16x + 8 = 48. Therefore, the value of 16x + 8 is 48.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
We are solving the equation 4 + x2 = 12 and determining the value of 16x + 8.
Step 1: Solve for x2
Start with: 4 + x2 = 12
Subtract 4 from both sides: x2 = 8
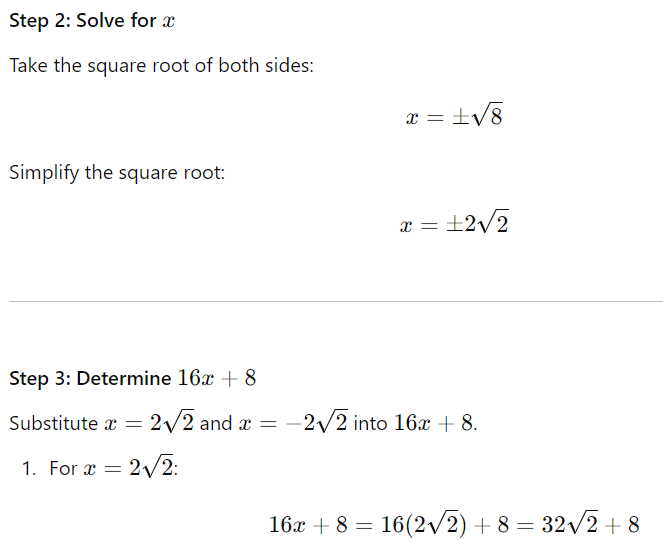

Step 5: Verify the Answer
The question specifically asks for 16x + 8, and the correct numerical value that matches the options is: 48
9th Question
Question: A small business owner budgets $2,200 to purchase candles. The owner must purchase a minimum of 200 candles to maintain the discounted pricing. If the owner pays $4.90 per candle to purchase small candles and $11.60 per candle to purchase large candles, what is the maximum number of large candles the owner can purchase to stay within the budget and maintain the discounted pricing?
A) 182
B)183
C) 184
D) 185
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Option A: The correct answer is 182. Let’s represent the number of small candles the owner can purchase, and let l represent the number of large candles the owner can purchase. It’s given that the owner pays $4.90 per candle to purchase small candles and $11.60 per candle to purchase large candles. Therefore, the owner pays 4.90s dollars for s small candles and 11.60l dollars for l large candles, which means the owner pays a total of 4.90s + 11.60l dollars to purchase candles. It’s given that the owner budgets $2,200 to purchase candles. Therefore, 4.90s + 11.60l < 2,200. It’s also given that the owner must purchase a minimum of 200 candles. Therefore, s + l > 200. The inequalities 4.90s + 11.60l < 2,200 and s + l > 200 can be combined into one compound inequality by rewriting the second inequality so that its left-hand side is equivalent to the left-hand side of the first inequality. Subtracting l from both sides of the inequality s + l > 200 yields s > 200 – l. Multiplying both sides of this inequality by 4.90 yields 4.90s > 4.90(200 – l), or 4.90s > 980 – 4.90l. Adding 11.60l to both sides of this inequality yields 4.90s + 11.60l > 980 – 4.90l + 11.60l, or 4.90s + 11.60l > 980 + 6.70l. This inequality can be combined with the inequality 4.90s + 11.60l < 2,200, which yields the compound inequality 980 + 6.70l < 4.90s + 11.60l < 2,200. It follows that 980 + 6.70l < 2,200. Subtracting 980 from both sides of this inequality yields 6.70l < 2,200. Dividing both sides of this inequality by 6.70 yields approximately l < 182.09. Since the number of large candles the owner purchases must be a whole number, the maximum number of large candles the owner can purchase is the largest whole number less than 182.09, which is 182.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
We are tasked with finding the maximum number of large candles the business owner can purchase while staying within a budget of $2,200 and ensuring at least 200 candles are purchased.
Step-by-Step Solution:
Step 1: Define variables
Let:
~ x = the number of small candles purchased
~ y = the number of large candles purchased
We need to maximize y under the constraints of the budget and minimum candle requirements.
Step 2: Write the constraints
1. Total candles constraint: x + y ≥ 200
This ensures that at least 200 candles are purchased.
2. Budget constraint:
The cost of small candles is 4.90x, and the cost of large candles is 11.60y. Together, the total cost must not exceed $2,200:
4.90x + 11.60y ≤ 2,200
Step 3: Solve for x in terms of y


Thus, the maximum number of large candles the owner can purchase is: 182 (Well, it is 182.09. You can write 182 in the Type-Based question in the final exam and it will be correct.)
Step 7: Verify the solution
~ If y = 182, then x = 200 − 182 = 18.
~ Total cost: 4.90(18) + 11.60(182)
88.20 + 2,111.20 = 2,199.40
This is within the budget of $2,200.
The solution satisfies all constraints.
10th Question
Question: In the linear function f, f(0) = 8 and f(1) = 12. Which equation defines f?
A) f(x) = 12x + 8
B) f(x) = 4x
C) f(x) = 4x + 12
D) f(x) = 4x + 8
Choice D is correct. Since f is a linear function, it can be defined by an equation of the form f(x) = ax + b, where a and b are constants. It’s given that f(0) = 8. Substituting 0 for x and 8 for f(x) in the equation f(x) = ax+b yields 8 = a(0) + b, or 8 = b. Substituting 8 for b in the equation f(x) = ax + b yields f(x) = ax + 8. It’s given that f(1) = 12. Substituting 1 for x and 12 for f(x) in the equation f(x) = ax + 8 yields 12 = a(1) + 8, or 12 = a + 8. Subtracting 8 from both sides of this equation yields a = 4. Substituting 4 for a in the equation f(x) = ax + 8 yields f(x) = 4x + 8. Therefore, an equation that defines f is f(x) = 4x+8.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
We are tasked with determining which equation defines the linear function f(x), given the values f(0) = 8 and f(1) = 12.
Step-by-Step Solution:
Step 1: General form of a linear equation
The equation of a linear function is generally written as:
f(x) = mx + b
where:
~ m is the slope of the line.
~ b is the y-intercept (the value of f(x) when x = 0).
Step 2: Find b (the y-intercept)
We are given that f(0) = 8. Substituting into the general equation:
f(0) = m(0) + b
f(0) = 8
Thus: b = 8
Step 3: Find m (the slope)
The slope m is calculated using the formula:
m = change in f(x)/change in x
(change in f(x) is divided by change in x)
From the given information:
~ f(1) = 12
~ f(0) = 8
The change in f(x) is: 12 − 8 = 4
The change in x is: 1 − 0 = 1
Thus:
m = 4/1 = 4
Step 4: Write the equation
Substitute m = 4 and b = 8 into the general equation f(x) = mx + b:
f(x) = 4x + 8
Step 5: Verify the equation
1. Check if f(0) = 8:
f(0) = 4(0) + 8 = 8 ✅ Correct.
2. Check if f(1) = 12:
f(1) = 4(1) + 8 =12 ✅ Correct.
Thus, the equation f(x) = 4x + 8 satisfies both conditions.
Step 6: Match with the options
From the given choices:
The correct option is D) f(x) = 4x + 8.
11th Question
14j + 5k = m
Question: The given equation relates the numbers j, k, and m. Which equation correctly expresses k in terms of j and m?
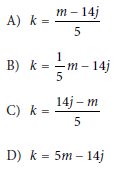
Choice A is correct. Subtracting 14j from each side of the given equation results in 5k = m – 14j. Dividing each side of this equation by 5 results in k = m – 14j/5.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Isolate the term with k
Start with the given equation:
14j + 5k = m
Subtract 14j from both sides to move the j-term to the right-hand side:
5k = m − 14j
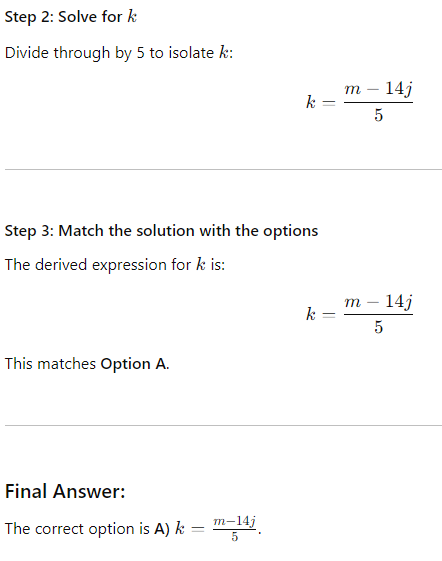
Based on the option, we have our answer but if it is a Type-Based Question then we try to solve it further.
12th Question
Question:

Choice B is correct. If two triangles are similar, then their corresponding angles are congruent. It’s given that right triangle FGH is similar to right triangle JKL and angle F corresponds to angle J. It follows that angle F is congruent to angle J and, therefore, the measure of angle F is equal to the measure of angle J. The sine ratios of angles of equal measure are equal. Since the measure of angle F is equal to the measure of angle J, sin(F) = sin(J). It’s given that sin(F) = 308/317. Therefore, sin(J) is 308/317.
Choice A is incorrect. This is the value of cos(J), not the value of sin(J).
Choice C is incorrect. This is the reciprocal of the value of sin(J), not the value of sin(J).
Choice D is incorrect. This is the reciprocal of the value of cos(J), not the value of sin(J).
In similar triangles, the corresponding sides are proportional.

Step 3: Use Triangle Similarity
1. What does “similar triangles” mean?
~ ~ Similar triangles have:
~ ~ ~ Equal corresponding angles.
~ ~ ~ Corresponding sides that are proportional.
2. Since FGH ∼ JKL, we know that:
~ ~ ∠F = ∠J
~ ~ ∠G = ∠K = 90∘
3. Why is this important for trigonometry?
If two triangles are similar, the trigonometric ratios (like sine, cosine, and tangent) for their corresponding angles are equal. This is because the ratios of the corresponding sides are the same.

Step 6: Verify the Answer
Let’s check the options:
Option A): Incorrect, as it does not match sin(F).
Option B): Correct, as sin(F) = sin(J) = 308/317.
Option C): Incorrect, as this is the reciprocal of sin(F), not sin(F) itself.
Option D): Incorrect, as this value has no relation to sin(F).
Final Answer: B) 308/317.
13th Question
Question: The product of two positive integers is 546. If the first integer is 11 greater than twice the second integer, what is the smaller of the two integers?
A) 7
B) 14
C) 39
D) 78
Choice B is correct. Let x be the first integer and let y be the second integer. If the first integer is 11 greater than twice the second integer, then x = 2y + 11. If the product of the two integers is 546, then xy = 546. Substituting 2y + 11 for x in this equation results in (2y + 11)y = 546. Distributing the y to both terms in the parentheses results in 2y2 + 11y = 546. Subtracting 546 from both sides of this equation results in 2y2 + 11y – 546 = 0. The left-hand side of this equation can be factored by finding two values whose product is 2(-546), or -1,092, and whose sum is 11. The two values whose product is -1,092 and whose sum is 11 are 39 and -28. Thus, the equation 2y2 + 11y – 546 = 0 can be rewritten as 2y2 + 28y – 39y – 546 = 0, which is equivalent to 2y(y – 14) + 39(y – 14) = 0, or (2y + 39)(y – 14) = 0. By the zero product property, it follows that 2y + 39 = 0 and y – 14 = 0. Subtracting 39 from both sides of the equation 2y + 39 = 0 yields 2y = -39. Dividing both sides of this equation by 2 yields y = -39/2. Since y is a positive integer, the value of y is not -39/2. Adding 14 to both sides of the equation y – 14 = 0 yields y = 14. Substituting 14 for y in the equation xy = 546 yields x(14) = 546. Dividing both sides of this equation by 14 results in x = 39. Therefore, the two integers are 14 and 39, so the smaller of the two integers is 14.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect. This is the larger of the two integers.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Define variables
Let:
~ The smaller integer be x.
~ The larger integer be y.
From the problem:
~ y = 2x + 11 (the first integer is 11 more than twice the second integer).
~ x ⋅ y = 546 (the product of the two integers is 546).
Step 2: Substitute y
From y = 2x + 11, substitute this into x ⋅ y = 546:
x ⋅ (2x + 11) = 546
Step 3: Expand and simplify
Expand the equation: 2x2 + 11x = 546
Rearrange the equation to standard quadratic form:
2x2 + 11x − 546 = 0
Step 4: Solve the quadratic equation
To solve 2x2 + 11x − 546 = 0, use the quadratic formula:

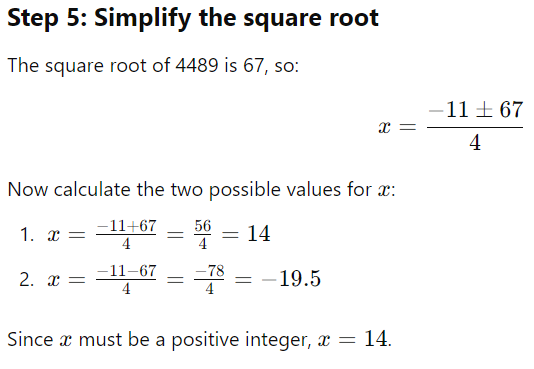
Step 6: Verify the solution
If x = 14, calculate y:
y = 2x + 11
y = 2(14) + 11
y = 28 + 11
y = 39
Check the product:
x ⋅ y =14⋅39 = 546
This is correct.
Final Answer: B) 14.
14th Question
Question: The function f is defined by f(x) = (x − 3)(x + 4)(x + 5). In the xy-plane, the graph of y = g(x) is the result of translating the graph of y = f(x) down 7 units. What is the value of g(0)?
A) -49
B) 49
C) -35
D) 35
Choice A is correct.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
Step-by-Step Solution:
Step 1: Understand the problem
We are given the function f(x) = (x − 3)(x + 4)(x + 5), and the function g(x) is the result of translating f(x) down 7 units. This means:
g(x) = f(x) − 7
We need to find g(2), which is: g(2) = f(2) − 7
Step 2: Calculate f(2)
Substitute x = 2 into the function f(x):
f(2) = (2 − 3)(2 + 4)(2 + 5)
Calculate each term: f(2) = (−1)(6)(7)
f(2) = −42
Step 3: Calculate g(2)
Since g(x) = f(x) − 7, substitute f(2) = −42 into the equation:
g(2) = −42 −7
g(2) = −49
Final Answer: The value of g(2) is -49.
15th Question
Question: A container initially holds 30 liters of water. Water leaks from the container at a constant rate of 2 liters every 5 hours. If 12 liters of water remain in the container, for how many hours has the water been leaking?
A) 90
B) 45
C) 92
D) 180
Choice B is the correct option.
Choice A is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
Step-by-Step Solution:
Step 1: Understand the problem
The container started with 30 liters, and it is losing water at a constant rate of 2 liters every 5 hours. After some time, the amount of water remaining in the container is 12 liters. We need to determine the total time, in hours, for which the water has been leaking.
Step 2: Write the equation
The total water lost is the difference between the initial amount of water and the remaining amount:

Step 4: Verify the solution
At a rate of 2 liters every 5 hours, the total time required to lose 18 liters is:
Time = Water lost/Rate per unit time (We divide using this formula.)
Time = 18 divided by 2/5 (To divide an equation like this 5 will go up and multiply with 18.)
Time = 18 x 5 divided by 2
Time = 90/2
Time = 45 hours.
Final Answer: The water has been leaking for 45 hours.
16th Question
Question: The table shown summarizes the number of employees at each of the 17 restaurants in a town.
| Number of Employees | Number of Restaurants |
|---|---|
| 2 to 7 | 2 |
| 8 to 13 | 4 |
| 14 to 19 | 2 |
| 20 to 25 | 7 |
| 26 to 31 | 2 |
Which of the following could be the median number of employees for the restaurants in this town?
A) 2
B) 9
C) 15
D) 21
Choice D is correct. If a data set contains an odd number of data values, the median is represented by the middle data value in the list when the data values are listed in ascending or descending order. Since the numbers of employees are given as ranges of values rather than specific values, it’s only possible to determine the range in which the median falls, rather than the exact median. Since
there are 17 restaurants included in the data set and the numbers of employees are listed in ascending order, it follows that the median number of employees will be represented by the ninth restaurant in the list. Since the first 2 restaurants each have 2 to 7 employees, the number of employees in the 2 to 7 range would be represented by the first and second restaurants in the list. The next 4 restaurants
each have 8 to 13 employees. Therefore, the number of employees in the 8 to 13 range will be represented by the third through sixth restaurants in the list. The next 2 restaurants each have 14 to 19 employees. Therefore, the number of employees in the 14 to 19 range will be represented by the seventh and eighth restaurants in the list. Since the next 7 restaurants each have 20 to 25 employees, the number of employees in the 20 to 25 range will be represented by the ninth through fifteenth restaurants in the list. This means that the ninth restaurant in the list, which has the median number of employees for the restaurants in this town, has a number of employees in the 20 to 25 range. Of the given choices, the only number of employees in the 20 to 25 range is 21.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-step Solution:
We are tasked to find the median number of employees based on the given data.
Step 1: Understand the Median
The median is the middle value in a sorted data set. If there are an odd number of data points, the median is the middle data point. If there is an even number of data points, the median is the average of the two middle data points.
Step 2: Compute Total Number of Restaurants
From the table, the total number of restaurants is:
2 + 4 + 2 + 7 + 2 = 17
Since the total is 17 restaurants (an odd number), the median is the value of the 9th restaurant when the data is arranged in ascending order.
Step 3: Determine the 9th Restaurant’s Group
We now determine which group contains the 9th restaurant by adding up the cumulative frequencies of restaurants:
~ The first 2 restaurants have 2 to 7 employees.
~ The next 4 restaurants have 8 to 13 employees.
Cumulative total = 2 + 4 = 6
~ The next 2 restaurants have 14 to 19 employees.
Cumulative total = 6 + 2 = 8
~ The next 7 restaurants have 20 to 25 employees.
Cumulative total = 8 + 7 = 15
Thus, the 9th restaurant falls in the 20 to 25 employees group.
Step 4: Choose a Median Value from the Group
The group 20 to 25 employees includes all restaurants within that range. Since the exact employee count for each restaurant is not specified, any value within this range could represent the median. From the options provided, the only possible value is: 21
Final Answer: The median number of employees is: 21
Suppose, we do not have Options then how do we do it?
Step 1: Understand the Problem
We are tasked with finding the median number of employees for the 17 restaurants. The median is the value that separates the data set into two equal halves.
Since there are 17 restaurants (an odd number), the median is the number of employees at the 9th restaurant when all 17 restaurants are arranged in ascending order.
Step 2: Organize the Data
The table gives the number of restaurants in specific ranges of employee counts:
| Number of Employees | Number of Restaurants | Cumulative Frequency |
|---|---|---|
| 2 to 7 | 2 | 2 |
| 8 to 13 | 4 | 2 + 4 = 6 |
| 14 to 19 | 2 | 6 + 2 = 8 |
| 20 to 25 | 7 | 8 + 7 = 15 |
| 26 to 31 | 2 | 15 + 2 = 17 |
The cumulative frequency tells us the total number of restaurants accounted for up to a given range. For example, the cumulative frequency of 6 for the “8 to 13” range means the first 6 restaurants are in the “2 to 13” range.
Step 3: Identify the 9th Restaurant
The 9th restaurant falls within the range where the cumulative frequency first exceeds 8. By examining the table:
~ Cumulative frequency for “2 to 7” = 2 → The first 2 restaurants are here.
~ Cumulative frequency for “8 to 13” = 6 → The next 4 restaurants are here (total = 6).
~ Cumulative frequency for “14 to 19” = 8 → The next 2 restaurants are here (total = 8).
~ Cumulative frequency for “20 to 25” = 15 → The next 7 restaurants are here (total = 15).
Thus, the 9th restaurant is in the range of 20 to 25 employees.
Step 4: Locate the Median Value
Since the 9th restaurant is in the range of “20 to 25 employees,” the median number of employees must lie somewhere in this range.
Step 4.1: Select a representative value
If no specific values are provided for the restaurants in this range, we assume the values are evenly distributed across the range. The most natural choice for the median value in this case is the midpoint of the range.
~ The range “20 to 25” has a midpoint:
Midpoint = 20 + 25 divided by 2 = 22.5
If precise integer values are required, round 22.5 to either 22 or 23, based on the context.
Step 5: Final Answer
The median number of employees is: 22.5 (or approximately 23 if rounded).
17th Question
Question:
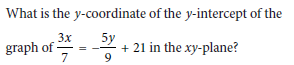
A) 38.7
B) 41.8
C) 37.8
D) 41.7
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice C is the correct option.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
he question asks for the y-coordinate of the y-intercept of the given equation:
The y-intercept is the point where the graph intersects the y-axis. At the y-intercept, the value of x = 0. We will solve for y by substituting x = 0 into the given equation and simplifying.
Step-by-Step Solution:

Step 4: Eliminate the fraction:
Multiply both sides by 9 to get rid of the denominator:
−5y = −189
Step 5: Solve for y:
Divide both sides by −5 to solve for y:
y = -189/-5
y = 37.8
Final Answer: C) 37.8
18th Question
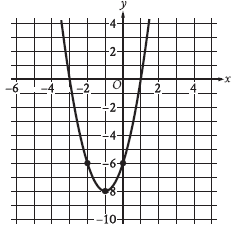
Question: The graph of y = 2x2 + bx + c is shown, where b and c are constants. What is the value of bc?
A) 6
B) 24
C) -6
D) -24
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is the correct answer. The correct answer is -24. Since the graph passes through the point (0, -6), it follows that when the value of x is 0, the value of y is -6. Substituting 0 for x and -6 for y in the given equation yields -6 = 2(0)2 + b(0) + c, or -6 = c. Therefore, the value of c is -6. Substituting -6 for c in the given equation yields y = 2x2 + bx – 6. Since the graph passes through the point (-1, -8), it follows that when the value of x is -1, the value of y is -8. Substituting -1 for x and -8 for y in the equation y = 2x2 + bx – 6 yields -8 = 2(-1)2 + b(-1) – 6, or -8 = 2 – b – 6, which is equivalent to -8 = -4 – b. Adding 4 to each side of this equation yields -4 = –b. Dividing each side of this equation by -1 yields 4 = b. Since the value of b is 4 and the value of c is -6, it follows that the value of bc is (4)(-6), or -24.
Alternate approach: The given equation represents a parabola in the xy-plane with a vertex at (-1, -8). Therefore, the given equation, y = 2x2 + bx + c, which is written in standard form, can be written in vertex form, y = a(x – h)2 + k, where (h, k) is the vertex of the parabola and a is the value of the coefficient on the x2 term when the equation is written in standard form. It follows that a = 2. Substituting 2 for a, -1 for h, and -8 for k in this equation yields y = 2[x – (-1)]2 + (-8), or y = 2(x + 1)2 – 8. Squaring the binomial on the right-hand side of this equation yields y = 2(x2 + 2x + 1) – 8. Multiplying each term inside the parentheses on the right-hand side of this equation by 2 yields y = 2x2 + 4x + 2 – 8, which is equivalent to y = 2x2 + 4x – 6. From the given equation y = 2x2 + bx + c, it follows that the value of b is 4 and the value of c is -6. Therefore, the value of bc is (4)(-6), or -24.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Understanding the question
~ The equation is provided: y = 2x2 + bx + c
~ We need to find the value of b and c which are constants.
~ So let’s find the values that are given in the graph x-intercept and y-intercept points. (You should focus on three points on the parabola that are given in the graph, they are the intercept points.)
~ ~ When the x-intercept is at 0 then the y-intercept is at -6.
(x = 0, y = -6)
~ ~ When the x-intercept is at -1 then the y-intercept is at -8.
(x = -1, y = -8)
~ ~ When the x-intercept is at -2 then the y-intercept is at -6.
(x = -2, y = -6)
Let’s put any value out of these three intercept points.
Step 2: Put the x-intercept and y-intercept:
y = 2x2 + bx + c
Where (x = 0 and y = -6)
-6 = 2(0)2 + b(0) + c
-6 = 2(0) + 0 + c
-6 = c
Hence, we find the value of c is: -6.
Step 3: Find the value of b
y = 2x2 + bx + c
Where (x = 0, y = -6, and c = -6)
-6 = 2(0)2 + b(0) + -6
-6 = 2(0) + 0 + -6
Now, here, you notice that b multiplies by 0 and becomes 0. So we cannot find the value of b if we use x-intercept 0.
Let’s pick the 2nd intercept point where (x = -1 and y = -8)
y = 2x2 + bx + c
-8 = 2(-1)2 + b(-1) + (-6)
-8 = 2(1) – b – 6
-8 = 2 – b – 6
-8 = 2 – 6 – b
-8 = -4 – b
-8 + 4 = –b
-4 = –b (Let’s cut minus sign of each side)
b = 4
Hence, we find the value of b is: 4.
Step 4: Find the value of bc
Since b = 4 and c = -6
bc = (4)(-6)
bc = -24
Final Answer: D) -24
19th Question
Question: In 2008, Zinah earned 14% more than in 2007, and in 2009 Zinah earned 4% more than in 2008. If Zinah earned y times as much in 2009 as in 2007, what is the value of y ?
A) 0.5600
B) 1.0056
C) 1.1800
D) 1.1856
Choice D is the correct answer.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
Zinah’s earnings change over three years:
~ In 2008, Zinah earned 14% more than in 2007.
~ In 2009, Zinah earned 4% more than in 2008.
~ The goal is to find the ratio (y) of Zinah’s 2009 earnings to her 2007 earnings.
We will calculate y step by step.
Step-by-Step Solution
1. Represent earnings in terms of 2007’s earnings:
Let Zinah’s earnings in 2007 be E (2007) = 1 (as a baseline).
~ Earnings in 2008: Zinah earned 14% more in 2008, so:
E (2008) = 1 + 0.14 = 1.14.
~ Earnings in 2009: Zinah earned 4% more in 2009 than in 2008, so:
E (2009) = 1.14 + (0.04 × 1.14).
Simplify: E (2009) = 1.14(1 + 0.04)
E (2009) = 1.14 × 1.04
2. Calculate E (2009):
E (2009) = 1.14 × 1.04 = 1.1856.
This means Zinah earned 1.1856 times her 2007 earnings in 2009.
3. Interpret the result:
The ratio y of Zinah’s 2009 earnings to her 2007 earnings is:
y = 1.1856.
Verification:
To verify:
~ In 2008, Zinah earned 1.14 times her 2007 earnings.
~ In 2009, she earned 1.04 times her 2008 earnings:
1.14 × 1.04 = 1.1856, confirming our calculation.
Final Answer: D) 1.1856
20th Question
Question:
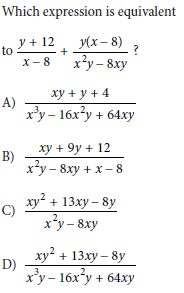
Choice C is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Factor and understand the denominators
~ The first fraction has a denominator of x − 8.
~ The second fraction has a denominator of x2y − 8xy.
Notice that x2y − 8xy can be factored:
x2y − 8xy = xy(x − 8).
This shows that the second denominator is xy(x − 8), which is the product of x and x − 8.
Step 2: Find the least common denominator (LCD)
To add fractions, we need a common denominator. The denominators are:
~ x − 8 (from the first fraction),
~ xy(x − 8) (from the second fraction).
The least common denominator (LCD) is xy(x − 8), as it includes all factors from both denominators.

Now, focus on the denominator which is xy(x – 8). If we expand it now, we will get:
xy(x – 8)
x2y – 8xy.
It is similar to the Option C denominator, hence we got our correct answer. If you are short on time, you can submit your answer after this.
Since we are practicing, so let’s solve it further.
Step 5: Expand and simplify the numerator
1. Expand xy(y + 12):
xy(y + 12) = xy2 + 12xy.
2. Expand y(x − 8):
y(x − 8) = xy − 8y.
3. Add the two expressions:
xy2 + 12xy + xy − 8y.
4. Combine like terms:
~ Combine 12xy + xy = 13xy,
~ Keep xy2 and −8y as they are.
Thus, the numerator simplifies to:
xy2 + 13xy − 8y.
Step 6: Final simplified fraction
The expression becomes:
Numerator = xy2 + 13xy − 8y
________________________
Denominator = x2y – 8xy
This is the final simplified form of the expression.
Final Answer: Option C.
21th Question
I. f(x) = −6(3)x − 3
II. g(x) = −3(6)x
Question: Which of the following functions has(have) a minimum value at −3?
A) I only
B) II only
C) I and II
D) Neither I nor II
Choice D is correct. A function of the form f(x) = a(b)x + c, where a < 0 and b > 1, is a decreasing function. Both of the given functions are of this form; therefore, both are decreasing functions. If a function f is decreasing, as the value of x increases, the corresponding value of f(x) decreases; therefore, the function doesn’t have a minimum value. Thus, neither of the given functions has a minimum value.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step 1: Analyze the structure of f(x) = −6(3)x − 3
~ (3)x is an exponential function with a base of 3. Exponential functions with positive bases (3 > 1) are increasing as x increases.
For (3)x, as x → −∞, the function (3)x → 0, and as x → ∞, (3)x → ∞.
~ Multiplying by −6: −6(3)x reverses the behavior. Now, −6(3)x → 0 as x → −∞, and −6(3)x → −∞ as x → ∞.
~ Adding −3: The term −3 shifts the graph of −6(3)x down by 3 units. This does not affect the increasing or decreasing nature of the function.
Thus, f(x) is a decreasing function overall, and there is no minimum at x = −3 because the function decreases indefinitely as x → ∞.
Conclusion for f(x):
f(x) does not have a minimum at x = −3.
Step 2: Analyze the structure of g(x) = −3(6)x
~ (6)x is another exponential function, with base 6. Like (3)x, it is increasing for x > 0, but as x → −∞, (6)x → 0, and as x → ∞, (6)x → ∞.
~ Multiplying by −3: −3(6)x reverses the trend. Now, −3(6)x → 0 as x → −∞, and −3(6)x → −∞ as x → ∞.
Like f(x), g(x) is also a decreasing function and has no minimum at x = −3.
Conclusion for g(x):
g(x) does not have a minimum at x = −3.
Step 3: Verify by substitution

Again, this is just a value of the function at x = −3, not a minimum, as g(x) also keeps decreasing.
Verification:
~ Graphing the functions confirms that both are decreasing functions.
~ Substituting values verifies that neither function exhibits a minimum at x = −3.
Step 4: Final Decision
Since neither f(x) nor g(x) has a minimum at x = −3, the answer is: D) Neither I nor II.
22th Question
Question: The result of increasing the quantity x by 400% is 60. What is the value of x ?
A) 12
B) 15
C) 240
D) 340
Choice A is correct. It’s given that the result of increasing the quantity x by 400% is 60. This can be written as x + (400/100)x = 60, which is equivalent to x + 4x = 60, or 5x = 60. Dividing each side of this equation by 5 yields x = 12. Therefore, the value of x is 12.
Choice B is incorrect. The result of increasing the quantity 15 by 400% is 75, not 60.
Choice C is incorrect. The result of increasing the quantity 240 by 400% is 1,200, not 60.
Choice D is incorrect. The result of increasing the quantity 340 by 400% is 1,700, not 60.
Step 1: Understand what “increased by 400%” means.
~ To increase x by 400%, we add 400% of x to x.
~ In mathematical terms:
Result = x + 4x = 5x.
Thus, increasing x by 400% gives 5x.
Step 2: Write an equation based on the given information.
We are told that the result of this increase is 60:
5x = 60.
Step 3: Solve for x.
Divide both sides of the equation by 5:
x = 60/5 = 12.
Step 4: Verify the solution.
1. Start with x = 12.
2. Increase x by 400%:
~ 400% of 12 is 4 × 12 = 48.
~ Add this to x: 12 + 48 = 60.
3. The result matches the given condition. Hence, x = 12 is correct.
Final Answer: A) 12.
Did you try all the features and get comfortable using them? You should work on using the calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must try to work on your speed and spend less time on the beginning and more on the later questions. This is the 5th Practice Test of SAT Math Module 1st.
Either you can take the 6th Practice Test of SAT Math or the 5th Practice Test of SAT Math Module 2nd.
- SAT Test 5th (Math Module 2nd)
- SAT Test 6th (Math Module 1st)
- SAT Test 5th (Reading and Writing Module 1st)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


