
Prepare for the SAT: Math Test Module 2nd with Simple Step-by-step Solutions
Have you taken the module 1st? If yes, then you are in the right place. This is the 5th Test of Module 2nd. We have designed a similar exam format with all the necessary features for you to become a master in Math. You take the SAT Test Module Second to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 2nd.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 2ND
The second module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 2nd are only difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 2nd. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH STUDY GUIDE AND PROBLEM SOLUTIONS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: There are 55 students in Spanish club. A sample of the Spanish club students was selected at random and asked whether they intend to enroll in a new study program. Of those surveyed, 20% responded that they intend to enroll in the study program. Based on this survey, which of the following is the best estimate of the total number of Spanish club students who intend to enroll in the study program?
A) 11
B) 20
C) 44
D) 55
Choice A is correct. It’s given that 20% of the students surveyed responded that they intend to enroll in the study program. Therefore, the proportion of students in Spanish club who intend to enroll in the study program, based on the survey, is 0.20. Since there are 55 total students in Spanish club, the best estimate for the total number of these students who intend to enroll in the study program is 55(0.20), or 11.
Choice B is incorrect. This is the best estimate for the percentage, rather than the total number, of students in Spanish club who intend to enroll in the study program.
Choice C is incorrect. This is the best estimate for the total number of Spanish club students who do not intend to enroll in the study program.
Choice D is incorrect. This is the total number of students in Spanish club.
Problem Analysis:
We are given the following information:
~ There are 55 students in the Spanish club.
~ A random sample of students was asked about their intent to enroll in a new study program.
~ 20% of those surveyed intend to enroll in the program.
We need to estimate the total number of Spanish club students who intend to enroll in the program based on this survey.
Step-by-Step Solution:
Step 1: Understand the meaning of percentages
A percentage is a way of expressing a number as a fraction of 100. The problem states that 20% of the sampled students intend to enroll in the study program. This percentage is applied to the total number of students in the Spanish club, which is 55.
Step 2: Convert the percentage to a decimal
To calculate 20% of a number, convert the percentage to a decimal by dividing it by 100:
20% = 20/100 = 0.2
Step 3: Multiply the total number of students by the decimal
Now, calculate the number of students who intend to enroll by multiplying the total number of students by 0.2:
Number of students intending to enroll = 55 × 0.2
Step 4: Perform the multiplication
55 × 0.2 = 11
This calculation shows that 11 students in the Spanish club are estimated to intend to enroll in the study program.
Verification:
Let’s verify the calculation:
1) Recheck percentage conversion: 20% = 0.2, which is correct.
2) Recheck multiplication: 55 × 0.2 = 11, which is accurate.
Thus, the estimate is correct.
Final Answer: The best estimate of the total number of Spanish club students who intend to enroll in the study program is: 11.
2nd Question
Question: Jay walks at a speed of 3 miles per hour and runs at a speed of 5 miles per hour. He walks for w hours and runs for r hours for a combined total of 14 miles. Which equation represents this situation?
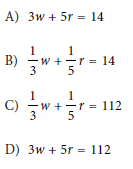
Choice A is correct. Since Jay walks at a speed of 3 miles per hour for w hours, Jay walks a total of 3w miles. Since Jay runs at a speed of 5 miles per hour for r hours, Jay runs a total of 5r miles. Therefore, the total number of miles Jay travels can be represented by 3w + 5r. Since the combined total number of miles is 14, the equation 3w + 5r = 14 represents this situation.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
Problem Analysis:
We are tasked with modeling the situation mathematically and identifying which equation represents it correctly. Here’s the information provided in the question:
1) Jay walks at a speed of 3 miles per hour.
2) Jay runs at a speed of 5 miles per hour.
3) Jay walks for w hours and runs for r hours.
4) The total distance covered is 14 miles.
We need to translate this situation into an equation.
Step-by-Step Explanation:
Step 1: Write an expression for distance traveled while walking
The formula for distance is:
Distance = Speed × Time.
~ Walking speed = 3 mph.
~ Walking time = w hours.
The distance Jay walks is: 3w.
Step 2: Write an expression for distance traveled while running
Running speed = 5 mph.
Running time = r hours.
The distance Jay runs is: 5r.
Step 3: Combine the distances
The total distance covered is the sum of the distance walked and the distance run:
Total distance = Walking distance + Running distance.
Substitute the expressions for walking and running distances:
Total distance = 3w + 5r.
We are told the total distance is 14 miles, so:
3w + 5r = 14.
Step 4: Match the correct equation
From the options given, the correct equation is: A) 3w + 5r = 14.
Verification:
1) Unit consistency: Both terms 3w and 5r represent distances (in miles). Their sum, 14, also represents a distance, which is consistent.
2) Logical interpretation: If Jay walks w hours at 3 mph and runs r hours at 5 mph, their combined distances equal the total distance traveled. This equation is logical.
Final Answer: A) 3w + 5r = 14.
3rd Question
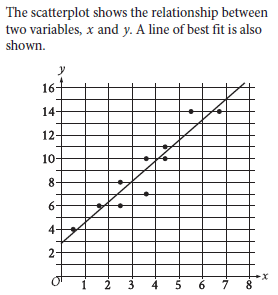
Question: Which of the following equations best represents the line of best fit shown?
A) y = 2.8 + 1.7x
B) y = 2.8 − 1.7x
C) y = −2.8 + 1.7x
D) y = −2.8 − 1.7x
Choice A is correct. The line of best fit shown intersects the y-axis at a positive y-value and has a positive slope. The graph of an equation of the form y = a + bx, where a and b are constants, intersects the y-axis at a y-value of a and has a slope of b. Of the given choices, only choice A represents a line that intersects the y-axis at a positive y-value, 2.8, and has a positive slope, 1.7.
Choice B is incorrect. This equation represents a line that has a negative slope, not a positive slope.
Choice C is incorrect. This equation represents a line that intersects the y-axis at a negative y-value, not a positive y-value.
Choice D is incorrect. This equation represents a line that intersects the y-axis at a negative y-value, not a positive y-value, and has a negative slope, not a positive slope.
Problem Analysis:
We are tasked with determining which equation best represents the line of best fit for the scatterplot provided.
The general form of the equation of a line is:
y = mx + b
where:
~ m is the slope of the line,
~ b is the y-intercept.
The question provides four options, each representing a possible equation. We will analyze the graph step-by-step and determine which equation is correct.
Step-by-Step Explanation:
Step 1: Identify the y-intercept (b)
The y-intercept is the point where the line of best fit crosses the y-axis (i.e., when x = 0).
From the graph:
~ The line of best fit crosses the y-axis at approximately 2.8.
~ Therefore, the b value (y-intercept) is 2.8.

Step 3: Determine the sign of the slope
The slope is positive because the line of best fit rises as x increases. This means that as x grows, y also grows.
This eliminates option B, which has a negative slope.
Remaining option:
A) y = 2.8 + 1.7x
Step 4: Verify the equation
Substitute a point from the line into the equation to verify:
Point (2, 6):
y = 2.8 + 1.7x
6 = 2.8 + 1.7(2)
6 = 2.8 + 3.4
6 = 6
This confirms that the equation is correct.
Final Answer: The equation of the line of best fit is: A) y = 2.8 + 1.7x.
4th Question
g(m) = -0.05m + 12.1
Question: The given function g models the number of gallons of gasoline that remains from a full gas tank in a car after driving m miles. According to the model, about how many gallons of gasoline are used to drive each mile?
A) 0.05
B) 12.1
C) 20
D) 242.0
Choice A is correct. It’s given that the function g models the number of gallons that remain from a full gas tank in a car after driving m miles. In the given function g(m) = -0.05m + 12.1, the coefficient of m is -0.05. This means that for every increase in the value of m by 1, the value of g(m) decreases by 0.05. It follows that for each mile driven, there is a decrease of 0.05 gallons of gasoline. Therefore, 0.05 gallons of gasoline are used to drive each mile.
Choice B is incorrect and represents the number of gallons of gasoline in a full gas tank.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
Problem Analysis:
We are tasked with interpreting the given linear function:
g(m) = −0.05m + 12.1
Where:
~ g(m): the number of gallons of gasoline remaining in the tank after driving m miles.
~ m: the number of miles driven.
The question asks: How many gallons of gasoline are used to drive each mile?
This is essentially asking us to determine the rate of change of the gallons of gasoline with respect to miles driven. The rate of change is represented by the slope of the equation.
Step-by-Step Explanation:
Step 1: Understand the structure of the equation
The equation g(m) = −0.05m + 12.1 is written in the slope-intercept form:
y = mx + b
Here:
~ m = −0.05: The slope of the line.
~ b = 12.1: The y-intercept, representing the number of gallons of gasoline in the tank when m = 0 (i.e., before driving any miles).
The slope m tells us how much the gallons of gasoline change per mile driven. Specifically:
m = Change in gallons of gasoline/Change in miles driven
Step 2: Interpret the slope
From the equation:
~ The slope is m = −0.05.
~ This means that for every additional mile driven (m increases by 1), the gallons of gasoline [g(m)] decrease by 0.05 gallons.
Thus, the car uses 0.05 gallons of gasoline per mile.
Step 3: Verify by substitution
Let us verify the interpretation using two points on the line:
1) Before driving (m = 0):
g(0) = −0.05(0) + 12.1
g(0) = 12.1 gallons.
This is the initial amount of gasoline in the tank.
2) After driving 1 mile (m = 1):
g(1) = −0.05(1) + 12.1
g(1) = −0.05 + 12.1
g(1) = 12.05 gallons.
The car has 12.05 gallons remaining after 1 mile.
The amount of gasoline used for 1 mile:
12.1 − 12.05 = 0.05 gallons.
This confirms that the car uses 0.05 gallons of gasoline per mile.
Final Answer: A) 0.05.
5th Question
Question:
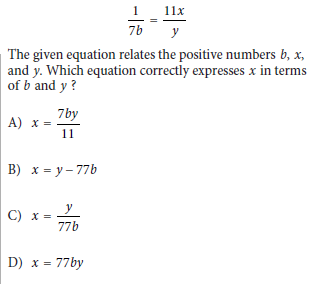
Choice C is correct. Multiplying each side of the given equation by y yields the equivalent equation y/7b = 11x. Dividing each side of this equation by 11 yields y/77b = x, or x = y/77b.
Choice A is incorrect. This equation is not equivalent to the given equation.
Choice B is incorrect. This equation is not equivalent to the given equation.
Choice D is incorrect. This equation is not equivalent to the given equation.
Step-by-Step Solution:
Step 1: Understand the equation
The equation relates four variables: b, x, y, and a constant. We aim to rewrite the equation so that x is isolated on one side of the equation.
Step 2: Eliminate the fractions
To eliminate the fractions, cross-multiply:
1 ⋅ y = 11x ⋅ 7b
This simplifies to:
y = 77bx
Step 3: Solve for x
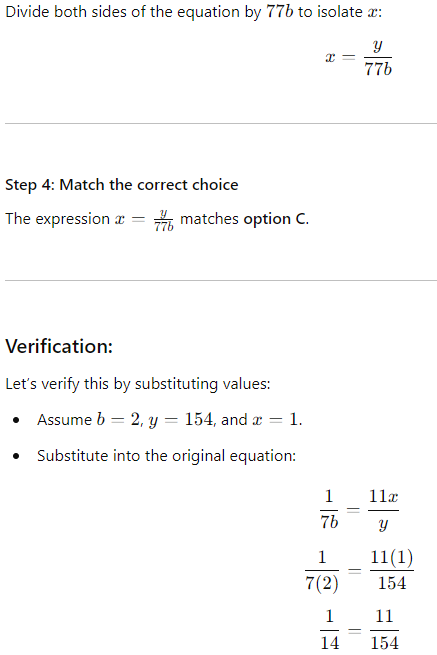
Both sides are equal, confirming the solution is correct.
Final Answer: C) x = y/77b.
6th Question
y = 76
y = x2 – 5
Question: The graphs of the given equations in the xy-plane intersect at the point (x, y). What is a possible value of x?
A) -76/5
B) −9
C) 5
D) 76
Choice B is correct. Since the point (x, y) is an intersection point of the graphs of the given equations in the xy-plane, the pair (x, y) should satisfy both equations, and thus is a solution of the given system. According to the first equation, y =76. Substituting 76 in place of y in the second equation yields x2 – 5 = 76. Adding 5 to both sides of this equation yields x2 = 81. Taking the square root of both sides of this equation yields two solutions: x = 9 and x = -9. Of these two solutions, only -9 is given as a choice.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the value of coordinate y, rather than x, of the intersection point (x, y).
Question Explanation and Detailed Solution
We are tasked with finding the value of xxx where the graphs of the given equations:
1) y = 76
2) y = x2 − 5
intersect in the xy-plane.

y = (−9)2 − 5
y = 81 − 5
y = 76
In both cases, y = 76, confirming that the intersection points are (9, 76) and (−9, 76).
Step 4: Answer
The possible values of x are:
x = 9 or x = −9
In the option, there is no positive 9, so we pick the negative 9.
Final Answer: B) -9.
7th Question
y > 14
4x + y < 18
Question: The point (x, 53) is a solution to the system of inequalities in the xy-plane. Which of the following could be the value of x?
A) −9
B) −5
C) 5
D) 9
Choice A is correct. It’s given that the point (x, 53) is a solution to the given system of inequalities in the xy-plane. This means that the coordinates of the point, when substituted for the variables x and y, make both of the inequalities in the system true. Substituting 53 for y in the inequality y > 14 yields 53 > 14, which is true. Substituting 53 for y in the inequality 4x + y < 18 yields 4x + 53 < 18. Subtracting 53 from both sides of this inequality yields 4x < -35. Dividing both sides of this inequality by 4 yields x < -8.75. Therefore, x must be a value less than -8.75. Of the given choices, only -9 is less than -8.75.
Choice B is incorrect. Substituting -5 for x and 53 for y in the inequality 4x + y < 18 yields 4(-5) + 53 < 18, or 33<18, which is not true.
Choice C is incorrect. Substituting 5 for x and 53 for y in the inequality 4x + y < 18 yields 4(5) + 53 < 18, or 73 < 18, which is not true.
Choice D is incorrect. Substituting 9 for x and 53 for y in the inequality 4x + y < 18 yields 4(9) + 53 < 18, or 89 < 18, which is not true.
Question Explanation and Solution
We are solving a system of inequalities:
1) y > 14
2) 4x + y < 18
The point (x, 53) satisfies the system. Our goal is to determine the possible value(s) of x.
Step 1: Analyze the Given Point in the First Inequality
Substitute y = 53 into the first inequality, y > 14:
53 > 14
This is true. Therefore, the point (x, 53) satisfies the first inequality.
Step 2: Substitute y = 53 in the Second Inequality
The second inequality is:
4x + y < 18
Substitute y = 53 into the inequality:
4x + 53 < 18
Simplify:
4x < 18 − 53
4x < −35
Divide both sides by 4 to isolate x:
x < −35/4
x < −8.75
Step 3: Interpret the Result
For the point (x, 53) to satisfy the system of inequalities, x must be less than −8.75. Therefore, any value of x < −8.75 is a solution.
We do not have any option of -8.75, but we know if some digit has more than 0.5 than it counts as 1. So, -8.75 becomes 9.
Final Answer: A) -9.
8th Question
Question: A gardener plants 250 seeds in her garden. If 72% of the seeds sprout, how many seeds sprouted?
A) 180
B) 168
C) 126
D) 72
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Write the Percent as a Decimal
Percentages can be converted to decimals by dividing by 100. Here, 72% becomes:
72% = 72/100 = 0.72
Step 2: Multiply the Decimal by the Total Number of Seeds
To find how many seeds sprouted, multiply the decimal 0.72 by the total number of seeds 250:
Number of sprouted seeds = 0.72 × 250
Step 3: Perform the Multiplication
0.72 × 250 = 180
So, 180 seeds sprouted.
Step 4: Verify the Answer
To verify, reverse the calculation. If 180 seeds sprouted, find the percentage:
Sprouted Seeds/Total Seeds = 180/250 = 0.72
Multiply by 100 to get the percentage:
0.72 × 100 = 72%
The calculation checks out.
Final Answer: A) 180.
9th Question
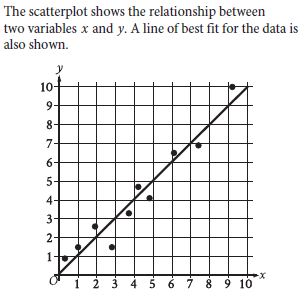
Question: For how many of the 10 data points is the actual y-value greater than the y-value predicted by the line of best fit?
A) 3
B) 4
C) 6
D) 7
Choice C is correct. Any data point that’s located above the line of best fit has a y-value that’s greater than the y-value predicted by the line of best fit. For the scatterplot shown, 6 of the data points are above the line of best fit. Therefore, 6 of the data points have an actual y-value that’s greater than the y-value predicted by the line of best fit.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect. This is the number of data points that have an actual y-value that’s less than the y-value predicted by the line of best fit.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis
The graph shows a scatterplot with 10 data points and a line of best fit. The question asks us to determine how many of the actual y-values for these points are greater than the y-values predicted by the line of best fit.
A point’s y-value is greater than the predicted value if the point lies above the line of best fit.
The line is the predicted y-value. The points are actual result.
Step 1: Analyze the Graph
Examine the placement of each data point relative to the line of best fit.
~ If a point is below the line, the actual y-value is less than the predicted y-value.
~ If a point is above the line, the actual y-value is greater than the predicted y-value.
Step 2: Count the Points Above the Line
From the scatterplot:
~ Points above the line are located at the following approximate (x, y)-coordinates:
There are total 6 points.
Final Answer: C) 6.
10th Question
Question: At a movie theater, there are a total of 350 customers. Each customer is located in either theater A, theater B, or theater C. If one of these customers is selected at random, the probability of selecting a customer who is located in theater A is 0.48, and the probability of selecting a customer who is located in theater B is 0.24. How many customers are located in theater C?
A) 28
B) 40
C) 84
D) 98
Choice D is correct. It’s given that at a movie theater, there are a total of 350 customers and that each customer is located in either theater A, theater B, or theater C. If the probability of selecting a customer in theater A is 0.48, then (0.48)(350), or 168, customers are located in theater A. If the probability of selecting a customer in theater B is 0.24, then (0.24)(350), or 84, customers are located in theater B. It follows that there are 168 + 84, or 252, customers in theater A and theater B. Therefore, there are 350 – 252, or 98, customers in theater C.
Choice A is incorrect. This is the percent, not the number, of the customers that are located in theater C.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect. This is the number of customers that are located in theater B, not theater C.
Step 1: Understand the Problem
The problem involves probability and requires us to determine the number of customers in theater C. The total number of customers is 350. Each customer is located in theater A, B, or C.
We are given:
~ P(A) = 0.48: Probability of selecting a customer in theater A.
~ P(B) = 0.24: Probability of selecting a customer in theater B.
The total probability of all customers must equal 1:
P(A) + P(B) + P(C) = 1
From this, we can find P(C):
P(C) = 1 − P(A) − P(B)
Once we find P(C), we use it to calculate the number of customers in theater C:
Number of customers in C = P(C) × Total customers.
Step 2: Solve for P(C)
Substitute P(A) = 0.48 and P(B) = 0.24 into the equation:
P(C) = 1 − 0.48 − 0.24
P(C) = 1 − 0.72
P(C) = 0.28
Thus, the probability of selecting a customer from Theater C is 0.28.
Step 3: Calculate the Number of Customers in Theater C
To find the number of customers in Theater C:
Number of customers in C = P(C) × Total customers
Number of customers in C = 0.28 × 350
Number of customers in C = 98
Step 4: Verify the Calculation
1) Check that the total number of customers is consistent:
~ Number of customers in A:
P(A) × Total customers = 0.48 × 350 = 168
~ Number of customers in B:
P(B) × Total customers = 0.24 × 350 = 84
~ Number of customers in C:
P(C) × Total customers = 0.28 × 350 = 98
2) Confirm the total matches 350:
168 + 84 + 98 = 350
The calculation is verified.
Final Answer: The number of customers in Theater C is: D) 98.
11th Question
Question: A cube has an edge length of 41 inches. What is the volume, in cubic inches, of the cube?
A) 164
B) 1,681
C) 10,086
D) 68,921
Choice D is correct. The volume, V, of a cube can be found using the formula V = s3, where s is the edge length of the cube. It’s given that a cube has an edge length of 41 inches. Substituting 41 inches for s in this equation yields V = 413 cubic inches, or V = 68,921 cubic inches. Therefore, the volume of the cube is 68,921 cubic inches.
Choice A is incorrect. This is the perimeter, in inches, of the cube.
Choice B is incorrect. This is the area, in square inches, of a face of the cube.
Choice C is incorrect. This is the surface area, in square inches, of the cube.
Step 1: Understand the Problem
The question asks us to find the volume of a cube with an edge length of 41 inches.
For a cube, all edges have equal length. The formula for the volume of a cube is:
V = s3
where s is the length of one edge.
Step 2: Calculate the Volume
Substitute the given edge length s = 41 inches into the formula:
V = 413
Step 3: Compute 413
Break down the calculation step by step:
413 = 41 × 41 × 41
1) Calculate 41 × 41:
41 × 41 = 1681
2) Multiply 1681 by 41:
1681 × 41 = 68921
Thus, the volume of the cube is:
V = 68921 cubic inches.
Step 4: Verify the Calculation
Double-check the math:
~ 41 × 41 = 1681 is correct (using distributive property:
41 × 41 = (40 + 1)(40 + 1)
=1600 + 40 + 40 + 1
= 1681.
~ 1681 × 41 is correct (using long multiplication or a calculator).
Final Answer: The volume of the cube is: D) 68921.
12th Question
p(t) = 90,000(1.65)t
Question: The given function p models the population of Lowell t years after a census. Which of the following functions best models the population of Lowell m months after the census?
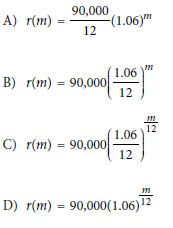
Choice D is correct. It’s given that the function p models the population of Lowell t years after a census. Since there are 12 months in a year, m months after the census is equivalent to m/12 years after the census. Substituting m/12 for t in the equation p(t) = 90,000(1.06)t yields p(m/12) = 90,000(1.06)m/12. Therefore, the function r that best models the population of Lowell m months after the census is r(m) = 90,000(1.06)m/12.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Problem
The function p(t) = 90,000(1.65)t models the population of Lowell t years after a census. However, we need to rewrite the function to model the population m, which represents months after the census. Since there are 12 months in a year, the relationship between t (years) and m (months) is:
t = m/12.
Step 2: Rewrite the Function in Terms of m
The original function is:
p(t) = 90,000(1.65)t.
Substitute t = m/12 into the function:
p(t) = 90,000(1.65)m/12.
Now the function becomes:
p(m) = 90,000(1.651/12)m.
This is equivalent to:
p(m) = 90,000[(1.651/12)]m.
Step 3: Compare the Options
We see that the structure of the function p(m) matches option D:
p(m) = 90,000 ⋅ (1.06)m,
where 1.06 represents 1.651/12, the monthly growth rate.
Step 4: Verify the Answer
To verify, calculate 1.651/12 using a calculator:
1.651/12 ≈ 1.06.
Thus, the answer matches the rewritten function exactly.
Final Answer: The function that best models the population m months after the census is: D) p(m) = 90,000(1.06)m.
13th Question
6x + 7y = 28
2x + 2y = 10
Question: The solution to the given system of equations is (x, y). What is the value of y?
A) −2
B) 7
C) 14
D) 18
Choice A is correct. The given system of linear equations can be solved by the elimination method. Multiplying each side of the second equation in the given system by 3 yields (2x + 2y)(3) = (10)(3), or 6x + 6y = 30. Subtracting this equation from the first equation in the given system yields (6x + 7y) – (6x + 6y) = (28) – (30), which is equivalent to (6x – 6x) + (7y – 6y) = 28 – 30, or y = -2.
Choice B is incorrect. This is the value of x, not the value of y.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Problem
We are solving the system of two linear equations:
1) 6x + 7y = 28
2) 2x + 2y = 10.
The goal is to determine the value of y in the solution (x, y) to this system of equations.
Step 2: Simplify the System
The second equation, 2x + 2y = 10, can be simplified by dividing through by 2:
x + y = 5.
This gives a simpler equivalent equation:
x + y = 5 (Equation 2 simplified).
Step 3: Solve for One Variable
From x + y = 5, solve for x in terms of y:
x = 5 − y.
Step 4: Substitute into the First Equation
Substitute x = 5 − y into the first equation 6x + 7y = 28:
6(5 − y) + 7y = 28.
Simplify:
30 − 6y + 7y = 28.
30 + y = 28.
y = 28 − 30.
y = −2.
Step 5: Verify the Solution
Now substitute y = −2 into both original equations to verify:
For the first equation:
6x + 7(−2) = 28.
6x – 14 = 28.
6x = 42.
x = 7.
For the second equation:
2(7) + 2(−2) = 10.
14 − 4 = 10.
Both equations are satisfied, so the solution is correct: (x, y) = (7, −2).
Final Answer: The value of y is: −2.
14th Question
| Number of Cars | Maximum Number of Passengers and Crew |
|---|---|
| 3 | 174 |
| 5 | 284 |
| 10 | 559 |
Question: The table shows the linear relationship between the number of cars, c, on a commuter train and the maximum number of passengers and crew, p, that the train can carry. Which equation represents the linear relationship between c and p?
A) 55c − p = −9
B) 55c − p = 9
C) 55p − c = −9
D) 55p − c = 9
Choice A is correct. It’s given that there is a linear relationship between the number of cars, c, on a commuter train and the maximum number of passengers and crew, p, that the train can carry. It follows that this relationship can be represented by an equation of the form p = mc + b, where m is the rate of change of p in this relationship and b is a constant. The rate of change of p in this relationship can be calculated by dividing the difference in any two values of p by the difference in the corresponding values of c. Using two pairs of values given in the table, the rate of change of p in this relationship is ‘284 – 174’ divided by ‘5 – 3,’ or 55. Substituting 55 for m in the equation p = mc + b yields p = 55c + b. The value of b can be found by substituting any value of c and its corresponding value of p for c and p, respectively, in this equation. Substituting 10 for c and 559 for p yields 559 = 55(10) + b, or 559 = 550 + b. Subtracting 550 from both sides of this equation yields 9 = b. Substituting 9 for b in the equation p = 55c + b yields p = 55c + 9. Subtracting 9 from both sides of this equation yields p – 9 = 55c. Subtracting p from both sides of this equation yields -9 = 55c – p, or 55c – p = -9.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
1. Understand the linear relationship:
The data shows a linear relationship, which means we can write it in the slope-intercept form:
p = mc + b
Where:
~ m is the slope (rate of change of p with respect to c).
~ b is the constant (value of p when c = 0).
2. Calculate the slope (m):
From the table:

Thus, the equation is:
p = 55c + 9
5. Rearrange into standard form:
To match the form in the options, rearrange p = 55c + 9 into standard form:
1) Subtract 9 from both sides: p − 9 = 55c
2) Subtract p from both sides: −9 = 55c − p
3) Rearrange for clarity: 55c − p = −9
6. Verify the equation:
Substitute other points into 55c − p = −9 to confirm. Use the point (3, 174):
55(3) − 174
=165 − 174
=−9
This is true.
Use the point (5, 284):
55(5) − 284
= 275 − 284
= −9
This is also true.
Thus, the equation is verified.
Final Answer: A) 55c − p = −9.
15th Question
Question:

A) 0.336
B) 0.292
C) 0.576
D) 0.616
Choice B is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
It is better if you start making progress on using the Desmos Calculator.

Step 3: Solve for c
Divide both sides of the equation by 8 to isolate c:
c = 7/3 ⋅ 8
c = 7/24.
Step 4: Decimal form of c
To find the decimal value of c, divide 7 by 24:
c = 7/24
c = 0.2916…
c = 0.292.

Final Answer: B) 0.292.
16th Question
Question: The graph of 9x − 10y = 19 is translated down 4 units in the xy-plane. What is the x-coordinate of the x-intercept of the resulting graph?
A) 5.99
B) 6.56
C) 7.67
D) 8.89
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 59/9. When the graph of an equation in the form Ax + By = C, where A, B, and C are constants, is translated down k units in the xy-plane, the resulting graph can be represented by the equation Ax + B(y + k) = C. It’s given that the graph of 9x – 10y = 19 is translated down 4 units in the xy-plane. Therefore, the resulting graph can be represented by the equation 9x – 10(y + 4) = 19, or 9x – 10y – 40 = 19. Adding 40 to both sides of this equation yields 9x – 10y = 59. The x-coordinate of the x-intercept of the graph of an equation in the xy-plane is the value of x in the equation when y = 0. Substituting 0 for y in the equation 9x – 10y = 59 yields 9x – 10(0) = 59, or 9x = 59. Dividing both sides of this equation by 9 yields x = 59/9. Therefore, the x-coordinate of the x-intercept of the resulting graph is 59/9. Note that 59/9, 6.555, and 6.556 are examples of ways to enter a correct answer.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Translate the Equation
The graph of 9x − 10y = 19 is translated down 4 units. This means we adjust the y-term of the equation. The general formula for translating a graph down k units is to replace y with y + k:
9x − 10(y + 4) = 19.
Distribute −10:
9x − 10y − 40 = 19.
Simplify:
9x − 10y = 59.
Step 2: Find the X-Intercept
The x-intercept occurs when y = 0. Substituting y = 0 into the translated equation 9x − 10y = 59:
9x − 10(0) = 59.
9x = 59.
Divide both sides by 9:
x = 59/9.
x = 6.555.
You can also write it as 6.56 or 6.6.
Thus, the x-coordinate of the x-intercept is 6.56.
Step 3: Verify the Reasoning
Let’s check the logic:
~ The graph was translated correctly using the equation 9x − 10(y + 4) = 19, which simplifies to 9x − 10y = 59.
~ Solving for the x-intercept by setting y = 0 yields x = 59/9, as required.
9x – 10y = 59
9x – 10(0) = 59
9x = 59
x = 59/9
x = 6.56.
Final Answer: The x-coordinate of the x-intercept of the resulting graph is: B) 6.56.
17th Question
Question: Two variables, x and y, are related such that for each increase of 1 in the value of x, the value of y increases by a factor of 4. When x = 0, y = 200. Which equation represents this relationship?
A) y = 4(x)200
B) y = 4(200)x
C) y = 200(x)4
D) y = 200(4)x
Choice D is correct. Since the value of y increases by a constant factor, 4, for each increase of 1 in the value of x, the relationship between x and y is exponential. An exponential relationship between x and y can be represented by an equation of the form y = a(b)x, where a is the value of x when y = 0 and y increases by a factor of b for each increase of 1 in the value of x. Since y = 200 when x = 0, a = 200. Since y increases by a factor of 4 for each increase of 1 in the value of x, b = 4. Substituting 200 for a and 4 for b in the equation y = a(b)x yields y = 200(4)x. Thus, the equation y = 200(4)x represents the relationship between x and y.
Choice A is incorrect and may result from conceptual errors.
Choice B is incorrect. This equation represents a relationship where for each increase of 1 in the value of x, the value of y increases by a factor of 200, not 4, and when x = 0, y is equal to 4, not 200.
Choice C is incorrect and may result from conceptual errors.
Step-by-Step Explanation
The problem describes a relationship where the value of y increases by a factor of 4 for every increase of 1 in x. This is an exponential relationship, and we are tasked with finding the equation that models this relationship, given that y = 200 when x = 0. Let’s break this down:
Step 1. General Form of an Exponential Function
The general form of an exponential equation is:
y = a ⋅ bx
~ a: The initial value of y when x = 0.
~ b: The base, or the factor by which y changes for each unit increase in x.
~ x: The independent variable.
Step 2. Identify the Values of a and b
~ From the problem, when x = 0, y = 200. This means a = 200.
~ The value of y increases by a factor of 4 for every unit increase in x. This means b = 4.
Substituting these values into the general form of the equation gives:
y = 200 ⋅ 4x
Step 3. Analyze the Answer Choices
Let’s evaluate the given options:
Option A: y = 4(x)200
This incorrectly uses 4 as the coefficient of x and raises x to the power of 200, which is not consistent with the exponential relationship described.
Option B: y = 4(200)x
This incorrectly reverses the roles of a and b, treating 200 as the base and 4 as the multiplier. This does not match the relationship where y grows by a factor of 4 for each increase of 1 in x.
Option C: y = 200(x)4
This incorrectly raises x to a power of 4, which implies a polynomial relationship rather than an exponential one.
Option D: y = 200(4)x
This correctly represents the relationship where y = 200 when x = 0, and y increases by a factor of 4 for each unit increase in x.
Step 4. Verify the Correct Answer
Let’s verify by substituting values of x into the correct equation y = 200(4)x:
~ When x = 0:
y = 200(4)0
y = 200(1)
y = 200
This matches the given initial value.
~ When x = 1:
y = 200(4)1
y = 200(4)
y = 800
y increases by a factor of 4, as expected.
~ When x = 2:
y = 200(4)2
y = 200(16)
y = 3200
Again, y grows by another factor of 4.
Thus, the correct answer is D: y = 200(4)x.
Final Anwer: D: y = 200(4)x.
18th Question
x2 – 2x – 9 = 0
Question:

Choice B is correct. Adding 9 to each side of the given equation yields x2 – 2x = 9. To complete the square, adding 1 to each side of this equation
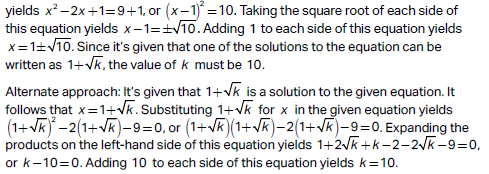
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
There are two ways to solve this equation:
1) Quadratic Formula

Now, we have our value.
Thus, the solution satisfies the equations.
Final Answer: B) 10.
2) Factoring Formula
1. Substituting the solution form into the equation:
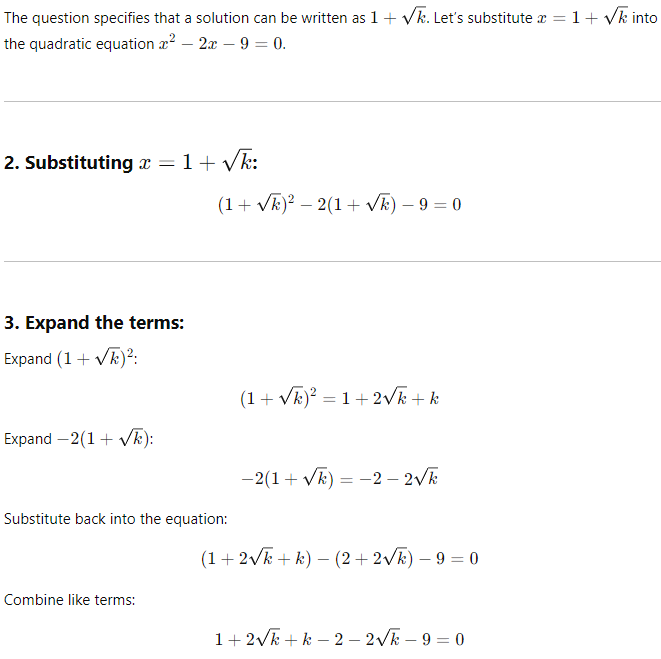
Simplify:
k − 10 = 0
4. Solve for k:
k = 10
5. Check if factoring is possible:
The original equation x2 − 2x − 9 = 0 does not factor neatly with integers. Therefore, factoring is not possible in this case. The alternate approach we used here relies on substitution and algebraic simplification.
Final Answer: B) 10.
19th Question
Question: Which quadratic equation has no real solutions?
A) x2 + 6x − 8 = 0
B) x2 − 6x + 8 = 0
C) 3x2 − 6x + 8 = 0
D) 3x2 − 6x – 8 = 0
Choice A is correct.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
To determine if a quadratic equation has real solutions, calculate the discriminant (Δ) of the quadratic equation. The quadratic equation in standard form is:
ax2 + bx + c = 0
The discriminant is given by:
Δ = b2 − 4ac
~ If Δ > 0, the equation has two distinct real solutions.
~ If Δ = 0, the equation has one real solution.
~ If Δ < 0, the equation has no real solutions.
Step 1: Analyze Each Option
Option A: x2 + 6x − 8 = 0
Here, a = 1, b = 6, and c = −8. Calculate Δ:
Δ = b2 − 4ac
Δ = 62 − 4(1)(−8)
Δ = 36 + 32
Δ = 68
Since Δ > 0, this equation has two distinct real solutions.
Option B: x2 − 6x + 8 = 0
Here, a = 1, b = −6, and c = 8. Calculate Δ:
Δ = b2 − 4ac
Δ = (−6)2 − 4(1)(8)
Δ = 36 − 32
Δ = 4
Since Δ > 0, this equation also has two distinct real solutions.
Option C: 3x2 − 6x + 8 = 0
Here, a =3, b = −6, and c = 8. Calculate Δ:
Δ = b2 − 4ac
Δ = (−6)2 − 4(3)(8)
Δ = 36 − 96
Δ = −60
Since Δ < 0, this equation has no real solutions.
Option D: 3x2 − 6x − 8 = 0
Here, a = 3, b = −6, and c = −8. Calculate Δ:
Δ = b2 − 4ac
Δ = (−6)2 − 4(3)(−8)
Δ = 36 + 96
Δ = 132
Since Δ > 0, this equation has two distinct real solutions.
Final Answer: The quadratic equation that has no real solutions is C) 3x2 − 6x + 8 = 0.
20th Question
p(t) = 150(1.03)(12/n)t
Question: The function models the population, in thousands, of a certain city t years after 2010. According to the model, the population is predicted to increase by 3% every n months. What is the value of n?
A) 6
B) 12
C) 18
D) 24
Choice B is correct.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Solution to the Different Question:
Step 1: Understand the exponential growth model
The general form of the exponential growth model is:
P(t) = P0(1 + r)kt
Where:
~ P0 = Initial population
~ r = Growth rate per compounding period
~ k = Number of compounding periods in one year
~ t = Time in years
In this case:
P(t) = 150(1.03)(12/n)t
Here, the growth rate is r = 0.03, and the exponent 12/n represents the number of compounding periods per year.
Step 2: Relate the growth rate to the compounding period
The model states that the population grows by 3% every n months. Since n months correspond to one compounding period, the number of compounding periods per year is:
k = 12/n
Step 3: Solve for n
To grow by 3% every n months, the base (1.03) already represents the growth factor per compounding period. Thus:
~ The compounding period corresponds directly to n months.
Since k = 12/n, we need k = 12/n = 1, which means the population grows every 12 months. Thus, n = 12.
Step 4: Verification
~ The base 1.03 indicates that the population grows by 3% per compounding period. The term 12/n in the exponent represents the number of compounding periods per year.
~ The problem specifies that the growth rate is 3% every n months, so we need to determine how many months (n) correspond to one compounding period.
~ To grow by 3% every n months, the total number of compounding periods in one year is:
k = 12/n
~ ~ From the equation P(t) = 150(1.03)(12/n)t, we see that the compounding growth is already expressed as a function of 12/n t.
~ ~ ~ Since 1.03 already accounts for growth per compounding period, we know there must be 12 months per compounding period for n.
Thus, n = 12.
~ If n = 12, then:
~ ~ k = 12/12 = 1.
~ ~ This means there is 1 compounding period per year, which matches the model’s interpretation that the population grows by 3% every n = 12 months.
Therefore, the population grows exactly once per year, and the solution is consistent.
The value of n is B) 12, which is correct.
Final Answer: The value of n is B) 12.
21th Question
Question: A circle in the xy-plane has its center at (3, −2). Line l is tangent to this circle at the point (7, 2). Which of the following points also lies on line l ?
A) (10, 6)
B) (8, 4)
C) (5, 0)
D) (6, 3)
Choice C is correct.
Choice D is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Slope of the Radius
The center is (3, −2) and the tangent point is (7, 2). The slope of the radius:

Not on the line.
3. (5, 0):
y = −5 + 9 = 4
But y = 4, but it should be y = 0, so it does not match.
Not on the line.
4. (6, 3):
y = −6 + 9 = 3.
This point lies on the line.
Optio D) (6, 3) is valid. If the options permit, choose either.
Final Answer: D) (6, 3).
22th Question
Question: An electric field with a strength of 50.00 volts/meter, passes uniformly through a flat surface perpendicular to the field. This surface is composed of two adjacent squares, where the side length of the larger square is 4 times the side length of the smaller square. If the total electric flux through the surface is 6,400 volts-meters, what is the electric flux through the smaller square?
A) 376.47
B) 487.64
C) 847.29
D) 1250.64
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A: The correct answer is 376.47 volts/meter.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the New Problem
The problem involves two squares:
~ The side length of the larger square is 4 times that of the smaller square.
~ The total electric flux through both squares is Φtotal = 6,400 volts-meters.
~ The electric flux (Φ) through each square is proportional to its area.
We need to find the electric flux through the smaller square.
Step 2: Represent Areas of the Squares

Final Answer: The electric flux through the smaller square is: A) 376.47 volts-meters.
Did you try all the features and get comfortable using them? You should work on using the Desmos calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must attempt as many questions as you can before the final test. This is the 5th Practice Test of SAT Math Module 2nd.
Either you can take the 6th Practice Test of SAT Math or the 6th Practice Test of SAT Reading and Writing Module 2nd.
- SAT Test 6th (Math Module 2nd)
- SAT Test 5th (Math Module 1st)
- SAT Test 5th (Reading and Writing Module 2nd)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


