
Attempt the SATs: Math Test with Real Examination Question, Detailed Explanation Module 2nd
Have you taken the module 1st? If yes, then you are in the right place. This is the 7th Test of Module 2nd. We have designed a similar exam format with all the necessary features for you to become a master in Math. You take the SAT Test Module Second to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 2nd.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 2ND
The second module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 2nd are only difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 2nd. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH STUDY GUIDE AND PROBLEM SOLUTIONS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: The function f is defined by f(x) = 8(x). For what value of x does f(x) = 72?
A) 8
B) 9
C) 64
D) 80
Choice B is correct. Substituting 72 for f(x) in the given function yields 72 = 8x. Dividing each side of this equation by 8 yields 9 = x. Therefore, f(x) = 72 when the value of x is 9.
Choice A is incorrect. This is the value of x for which f(x) = 64, not f(x) = 72.
Choice C is incorrect. This is the value of x for which f(x) = 512, not f(x) = 72.
Choice D is incorrect. This is the value of x for which f(x) = 640, not f(x) = 72.
Step-by-Step Explanation
We are tasked with solving for x in the function f(x) = 8x when f(x) = 72.
Step 1: Write Down the Given Function
The function is defined as:
f(x) = 8x.
We are given that:
f(x) = 72.
This means we need to solve the equation:
8x = 72.
Step 2: Solve for x
To isolate x, divide both sides of the equation by 8:
x = 72/8.
Simplify the division: x = 9.
Step 3: Verify the Solution
Substitute x = 9 back into the original function:
f(x) = 8x.
Substitute x = 9:
f(9) = 8(9) = 72.
This confirms that the solution is correct.
Final Answer: B) 9.
2nd Question
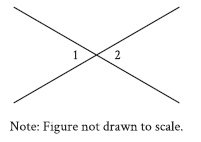
Question: In the figure, two lines intersect at a point. Angle 1 and angle 2 are vertical angles. The measure of angle 1 is 72°. What is the measure of angle 2?
A) 72°
B) 108°
C) 144°
D) 288°
Choice A is correct. It’s given that angle 1 and angle 2 are vertical angles, and the measure of angle 1 is 72°. Vertical angles have equal measures. Therefore, the measure of angle 2 is 72°.
Choice B is incorrect. This is the measure of an angle that is supplementary, not congruent, to angle 1.
Choice C is incorrect. This is the sum of the measures of angle 1 and angle 2.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation
We are given two intersecting lines, and angles 1 and 2 are vertical angles. The measure of angle 1 is 72°, and we are asked to find the measure of angle 2.
Step 1: Define Vertical Angles
Vertical angles are the angles formed opposite each other when two lines intersect. These angles are always equal in measure.
So, if angle 1 and angle 2 are vertical angles, then:
Measure of angle 1 = Measure of angle 2.
Step 2: Use the Given Information
From the problem, we know:
Measure of angle 1 = 72°.
Since angle 1 and angle 2 are vertical angles, their measures are equal. Therefore:
Measure of angle 2 = 72°.
Step 3: Verify the Answer
The definition of vertical angles ensures that their measures are equal. Thus, the measure of angle 2 is confirmed to be: 72°.
Final Answer: A) 72°.
3rd Question
Question: On a street with 7 houses, 2 houses are blue. If a house from this street is selected at random, what is the probability of selecting a house that is blue?
A) 1/7
B) 2/7
C) 5/7
D) 7/7
Choice B is correct. If a house from the street is selected at random, the probability of selecting a house that is blue is equal to the number of houses on the street that are blue divided by the total number of houses on the street. Since there are 2 blue houses on a street with 7 total houses, the probability of selecting a house that is blue from this street is 2/7.
Choice A is incorrect. This is the probability of selecting a house that is blue from a street on which 1 of the 7 houses is blue.
Choice C is incorrect. This is the probability of selecting a house that is not blue from this street.
Choice D is incorrect. This is the probability of selecting a house that is blue from a street on which all the houses are blue.
Step-by-Step Explanation
We are tasked with finding the probability of selecting a blue house at random on a street where there are 7 houses in total, and 2 houses are blue.
Step 1: Recall the Probability Formula

This means that if you randomly select a house from this street, the chance of it being blue is 2/7, or about 28.6%.
Step 4: Verify the Calculation
~ Number of blue houses: 2.
~ Total number of houses: 7.
Substituting into the formula confirms the calculation is correct.
Final Answer: B) 2/7.
4th Question
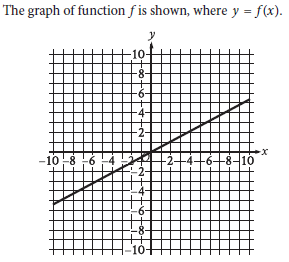
Question: Which of the following describes function f?
A) Increasing linear
B) Decreasing linear
C) Increasing exponential
D) Decreasing exponential
Choice A is correct. The graph of function f shows that as x increases, f(x) also increases, which means f(x) is an increasing function. The graph of f is a line, which indicates a constant rate of change. A function that has a constant rate of change is a linear function. Therefore, function f can be described as increasing linear.
Choice B is incorrect. For a decreasing function, as x increases, f(x) decreases, rather than increases.
Choice C is incorrect. For a decreasing function, as x increases, f(x) decreases, rather than increases, and the graph of an exponential function isn’t a line.
Choice D is incorrect. The graph of an exponential function isn’t a line.
Step 1: Understanding the Graph of Function f(x)
~ The graph represents the function y = f(x), plotted on a Cartesian plane.
~ It is a straight line that slants upward from left to right. This indicates that the function is linear (straight line) and increasing.
Step 2: Characteristics of the Graph
1. Increasing Function:
~ A function is increasing if the y-values rise as x-values increase.
~ Looking at the graph, as x moves from left to right, y becomes larger. This confirms that the function is increasing.
2. Linear Function:
~ A linear function has a constant rate of change, represented by a straight line on the graph.
~ Since the graph is a straight line, this is a linear function.
3. Exponential Functions (Ruled Out):
~ An exponential function f(x) = a ⋅ bx curves upward or downward, depending on whether b > 1 (increasing exponential) or 0 < b < 1 (decreasing exponential).
~ The graph in the question is a straight line, so it cannot represent an exponential function.
Step 3: Identifying the Correct Description
Based on the graph:
~ The function is increasing because y-values rise as x-values increase.
~ The function is linear because it forms a straight line.
Verification:
Let’s summarize:
~ The function is not exponential because the graph is a straight line.
~ The function is not decreasing because y rises as x increases.
~ Therefore, the correct description is “increasing linear.”
Final Answer: A) Increasing linear.
5th Question
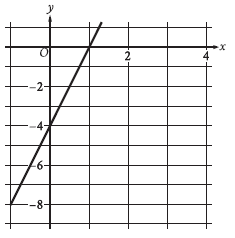
Question: The graph of the function f is shown, where y = f(x). What is the y-intercept of the graph?
A) (0, −1)
B) (0, −4)
C) (0, 1)
D) (0, 4)
Choice B is correct. The y-intercept of a graph is the point where the graph intersects the y-axis. The graph of function f shown intersects the y-axis at the point (0, -4). Therefore, the y-intercept of the graph is (0, -4).
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understanding the y-Intercept
The y-intercept of a graph is the point where the graph intersects the y-axis. At this point, the value of x is always 0. Therefore, to find the y-intercept, we need to determine the y-coordinate of the graph when x = 0.
Step 2: Analyzing the Graph
Looking at the graph:
~ The y-axis is the vertical axis.
~ The graph intersects the y-axis at the point (0, −4), meaning that when x = 0, y = −4.
Step 3: Verifying the Point
To confirm:
~ At x = 0, the graph clearly passes through y = −4, and no other y-value is plausible at this intersection.
Step 4: Answering the Question
The y-intercept of the graph is:
(0, −4)
Final Answer: B) (0, −4).
6th Question
|x – 5| = 10
Question: What is one possible solution to the given equation?
A) -15
B) -5
C) 10
D) 5
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 15 or -5. By the definition of absolute value, if |x – 5| = 10, then x – 5 = 10 or x – 5 = -10. Adding 5 to both sides of the first equation yields x = 15. Adding 5 to both sides of the second equation yields x = -5. Thus, the given equation has two possible solutions, 15 and -5. Note that 15 and –5 are examples of ways to enter a correct answer.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation
We are solving the equation ∣x − 5∣ = 10.
The absolute value equation ∣A∣ = B means that A can be either B or −B. This is because the absolute value of a number represents its distance from zero on the number line, and distance is always positive.
Step 1: Define the Absolute Value Expression
In the given equation:
∣x − 5∣ = 10
~ A = x − 5
~ B = 10
So, x − 5 can be either 10 or −10.
Step 2: Solve for x in Each Case
Case 1: x − 5 = 10
x − 5 = 10
Add 5 to both sides:
x = 15
Case 2: x − 5 = −10
x − 5 = −10
Add 5 to both sides: x = −5
Step 3: Verify the Solutions
We verify both solutions by substituting them back into the original equation ∣x − 5∣ = 10.
1) For x = 15:
∣15 − 5∣ = ∣10∣ = 10
This is true.
2) For x = −5:
∣−5 − 5∣ = ∣−10∣ = 10
This is also true.
Both solutions satisfy the equation.
Step 4: Provide One Solution
The question asks for one possible solution, so we can choose either:
x = 15 or x = −5.
Final Answer: B) -5.
7th Question
f(x) = 7x + 1
Question: The function gives the total number of people on a company retreat with x managers. What is the total number of people on a company retreat with 7 managers?
A) 50
B) 49
C) 30
D) 21
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 50. It’s given that the function f gives the total number of people on a company retreat with x managers. It’s also given that 7 managers are on the company retreat. Substituting 7 for x in the given function yields f(7) = 7(7) + 1, or f(7) = 50. Therefore, there are a total of 50 people on a company retreat with 7 managers.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation
We are given the function:
f(x) = 7x + 1
This function represents the total number of people on a company retreat, where x is the number of managers. The goal is to determine the total number of people on the retreat if there are x = 7 managers.
Step 1: Understand the Function
The function f(x) = 7x + 1 consists of two components:
1) 7x: This term represents the number of people associated with x managers, assuming that each manager brings 7 people to the retreat.
2) +1: This represents 1 additional person, likely someone who is not a manager (such as an organizer or a special guest).
Thus, the total number of people is calculated by multiplying the number of managers by 7 and adding 1.
Step 2: Substitute x = 7 into the Function
To find the total number of people when there are x = 7 managers:
f(7) = 7(7) + 1
Step 3: Simplify the Expression
1) Multiply 7 × 7:
7(7) = 49
2) Add 1:
49 + 1 = 50
Step 4: Verify the Interpretation
The function calculates the total number of people based on the number of managers and includes one additional person. Substituting x = 7 confirms that the total number of people is: 50.
Final Answer: A) 50.
8th Question
h(x) = x2 − 3
Question: Which table gives three values of x and their corresponding values of h(x) for the given function h?
A)
| x | 1 | 2 | 3 |
| h(x) | 4 | 5 | 6 |
B)
| x | 1 | 2 | 3 |
| h(x) | -2 | 1 | 6 |
C)
| x | 1 | 2 | 3 |
| h(x) | -1 | 1 | 3 |
D)
| x | 1 | 2 | 3 |
| h(x) | -2 | 1 | 3 |
Choice B is correct. It′s given that h(x) = x2 – 3. Each table gives 1, 2, and 3 as the three given values of x. Substituting 1 for x in the equation h(x) = x2 – 3 yields h(1) = x2 – 3, or h(1) = -2. Substituting 2 for x in the equation h(x) = x2 – 3 yields h(2) = (2)2 – 3, or h(2) = 1. Finally, substituting 3 for x in the equation h(x) = x2 – 3 yields h(3) = (3)2 – 3, or h(3) = 6. Therefore, h(x) is -2 when x is 1, h(x) is 1 when x is 2, and h(x) is 6 when x is 3. Choice B is a table with these values of x and their corresponding values of h(x).
Choice A is incorrect. This is a table of values for the function h(x) = x + 3, not h(x) = x2 – 3.
Choice C is incorrect. This is a table of values for the function h(x) = 2x – 3, not h(x) = x2 – 3.
Choice D is incorrect and may result from conceptual or calculation errors.
We are given the quadratic function:
h(x) = x2 − 3
Our task is to determine which table of values for x and h(x) corresponds to the function.
Step 1: Understand the Function
The given function h(x) = x2 − 3:
~ Takes an input x.
~ Squares the value of x.
~ Subtracts 3 from the squared result to calculate h(x).
We need to evaluate the function h(x) for x = 1, x = 2, and x = 3 and match the results to the corresponding table.
Step 2: Compute h(x) for Each Value of x
For x = 1:
Substitute x = 1 into the equation h(x) = x2 − 3:
h(1) = 12 − 3
= 1 − 3
= −2
For x = 2:
Substitute x = 2 into the equation h(x) = x2 − 3:
h(2) = 22 − 3
= 4 − 3
= 1
For x = 3:
Substitute x = 3 into the equation h(x) = x2 − 3:
h(3) = 32 − 3
= 9 − 3
= 6
Thus, the corresponding values of h(x) for x = 1, 2, 3 are:
h(1) = −2, h(2) = 1, h(3) = 6
Step 3: Match Results with the Answer Choices
The only table that matches these results is: Option B.
Step 4: Verify the Correctness of the Function
Rechecking the computations confirms that substituting each value of x into h(x) = x2 − 3 yields the values −2, 1, and 6. Thus, the answer is verified as correct.
Final Answer: Option B.
9th Question
Question: The function f is defined by f(x) = 270(0.1)x. What is the value of f(0)?
A) 0
B) 1
C) 27
D) 270
Choice D is correct. The value of f(0) is the value of f(x) when x = 0. Substituting 0 for x in the given function yields f(0) = 270(0.1)0, or f(0) = 270(1), which is equivalent to f(0) = 270. Therefore, the value of f(0) is 270.
Choice A is incorrect. This is the value of x, not f(x).
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect. This is the value of f(1), not f(0).
Problem Analysis
We are given the function f(x) = 270(0.1)x, and we are asked to find f(0). This requires substituting x = 0 into the function and evaluating it.
Step-by-Step Solution
1) Substitute x = 0 into the function:
The function is defined as:
f(x) = 270(0.1)x
Substituting x = 0:
f(0) = 270(0.1)0
2) Evaluate (0.1)0:
Any non-zero number raised to the power of 0 is equal to 1. Therefore:
(0.1)0 = 1
3) Simplify the expression:
Substitute (0.1)0 = 1 back into the equation:
f(0) = 270 × 1 = 270
Final Answer: The value of f(0) is: 270.
Verification
To confirm the correctness:
~ The rule a0 = 1 (for any a ≠ 0) ensures the evaluation of (0.1)0 = 1 is correct.
~ Substitution and simplification steps have been properly followed.
Final Answer: D) 270.
10th Question
Question: To estimate the proportion of a population that has a certain characteristic, a random sample was selected from the population. Based on the sample, it is estimated that the proportion of the population that has the characteristic is 0.49, with an associated margin of error of 0.04. Based on this estimate and margin of error, which of the following is the most appropriate conclusion about the proportion of the population that has the characteristic?
A) It is plausible that the proportion is between 0.45 and 0.53.
B) It is plausible that the proportion is less than 0.45.
C) The proportion is exactly 0.49.
D) It is plausible that the proportion is greater than 0.53.
Choice A is correct. It’s given that the estimate for the proportion of the population that has the characteristic is 0.49 with an associated margin of error of 0.04. Subtracting the margin of error from the estimate and adding the margin of error to the estimate gives an interval of plausible values for the true proportion of the population that has the characteristic. Therefore, it’s plausible that the proportion of the population that has this characteristic is between 0.45 and 0.53.
Choice B is incorrect. A value less than 0.45 is outside the interval of plausible values for the proportion of the population that has the characteristic.
Choice C is incorrect. The value 0.49 is an estimate for the proportion based on this sample. However, since the margin of error for this estimate is known, the most appropriate conclusion is not that the proportion is exactly one value but instead lies in an interval of plausible values.
Choice D is incorrect. A value greater than 0.53 is outside the interval of plausible values for the proportion of the population that has the characteristic.
Step-by-Step Solution
1) Understand the Proportion and Margin of Error
~ The estimated proportion of the population with the characteristic is 0.49.
~ The margin of error is 0.04.
~ The margin of error indicates the range of plausible values for the true proportion of the population with the characteristic.
2) Calculate the Range of Plausible Values
~ The range is determined by subtracting and adding the margin of error to the estimated proportion:
Lower bound = 0.49 − 0.04 = 0.45
Upper bound = 0.49 + 0.04 = 0.53
~ Therefore, the plausible range for the proportion is from 0.45 to 0.53.
3) Interpret Each Option
Option A: “It is plausible that the proportion is between 0.45 and 0.53.”
This is correct because the margin of error defines the range of plausible values as [0.45, 0.53].
Option B: “It is plausible that the proportion is less than 0.45.”
This is incorrect because the plausible range starts at 0.45. Values less than 0.45 are outside the margin of error.
Option C: “The proportion is exactly 0.49.”
This is incorrect because 0.49 is the estimate, not the exact value. The margin of error shows that the true proportion could vary within the range [0.45, 0.53].
Option D: “It is plausible that the proportion is greater than 0.53.”
This is incorrect because the plausible range ends at 0.53. Values greater than 0.53 are outside the margin of error.
4) Conclusion
The most appropriate conclusion is Option A: It is plausible that the proportion is between 0.45 and 0.53.
Verification
The solution follows the concept of interpreting a proportion and margin of error, which are commonly used in statistics. The plausible range [0.45, 0.53] is correctly calculated, and the options are accurately evaluated based on this range.
Final Answer: Option A.
11th Question
Question:
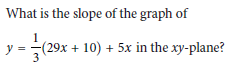
A) 44
B) 33.33
C) 17.44
D) 14.67
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 14.67. A linear equation can be written in the form y = mx + b, where m is the slope of the graph of the equation in the xy-plane and (0, b) is the y-intercept. Distributing the 1/3 in the equation y = 1/3 (29x + 10) + 5x yields y = 29/3 x + 10/3 + 5x. Combining like terms on the right-hand side of this equation yields y = 44/3 x + 10/3. This equation is in the form y = mx + b, where m = 44/3 and b = 10/3. Therefore, the slope of the graph of the given equation in the xy-plane is 44/3. Note that 44/3, 14.66, and 14.67 are examples of ways to enter a correct answer.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation

Step 5: Divide it
Let’s divide the value of m:
m = 44/3
m = 14.666
m = 14.67
Final Answer: D) 14.67.
12th Question
Question: The length of each edge of a box is 29 inches. Each side of the box is in the shape of a square. The box does not have a lid. What is the exterior surface area, in square inches, of this box without a lid?
A) 8,629
B) 6,667
C) 5,841
D) 4,205
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 4,205. The exterior surface area of a figure is the sum of the areas of all its faces. It’s given that the box does not have a lid and that each side of the box is in the shape of a square. Therefore, the box consists of 5 congruent square faces. It’s also given that the length of each edge is 29 inches. Let’s represent the length of an edge of a square. It follows that the area of a square is equal to s2. Therefore, the area of each of the 5 square faces is equal to 292, or 841, square inches. Since the box consists of 5 congruent square faces, it follows that the sum of the areas of all its faces, or the exterior surface area of this box without a lid, is 5(841), or 4,205, square inches.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Problem
The box is a cube-like structure, where:
~ Each edge of the box has a length of 29 inches.
~ Each side of the box is a square.
~ The box has 5 square sides because it does not have a lid.
We need to calculate the total exterior surface area of the box.
Step 2: Recall the Formula for the Area of a Square
The area of a square is given by:
Area of one square side = side2
Substitute the length of one side of the square (29):
Area of one square side = 292 = 841 square inches.
Step 3: Find the Total Area of 5 Sides
Since the box has 5 sides, we multiply the area of one square side by 5:
Total surface area = 5 ⋅ 841 = 4205 square inches.
Step 4: Verify the Calculations
~ First, calculate 292 = 841:
29 ⋅ 29 = 841, so the area of one square side is correct.
~ Then calculate 5 ⋅ 841 = 4205:
5 ⋅ 841 = 4205, confirming the total surface area.
Final Answer: The exterior surface area of the box without a lid is: D) 4205 square inches.
13th Question
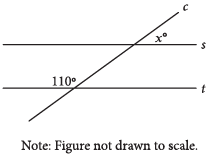
Question: In the figure shown, line c intersects parallel lines s and t. What is the value of x?
A) 110
B) 95
C) 70
D) 60
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice C is correct. The correct answer is 70. Based on the figure, the angle with measure 110° and the angle vertical to the angle with measure x° are same side interior angles. Since vertical angles are congruent, the angle vertical to the angle with measure x° also has measure x°. It’s given that lines s and t are parallel. Therefore, same side interior angles between lines s and t are supplementary. It follows that x + 110 = 180. Subtracting 110 from both sides of this equation yields x = 70.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Recognizing the Parallel Lines and Transversal
The figure shows that line c intersects two parallel lines, s and t. When a transversal intersects parallel lines, corresponding angles, alternate interior angles, and supplementary angles can be used to determine unknown angles.
Step 2: Identifying the Given Information
We are given:
~ A 110° angle on line t.
~ The angle x on line s, which we need to find.
Step 3: Using Corresponding Angles
Since s and t are parallel and c is the transversal:
~ The 110° angle on t is a corresponding angle to the angle on s, directly above x. Therefore, this corresponding angle is also 110°.
Step 4: Recognizing a Linear Pair
The angle x and the corresponding angle above it (110°) form a linear pair on line c. The sum of the angles in a linear pair is always 180°.
x + 110 = 180
Step 5: Solving for x
Subtract 110 from both sides:
x = 180 − 110 = 70
Final Answer: The value of x is: C) 70°.
14th Question
Question: A list of 10 data values is shown.
6, 8, 16, 4, 17, 26, 8, 5, 5, 5
What is the mean of these data?
A) 10
B) 16
C) 20
D) 22
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 10. The mean of a data set is calculated by dividing the sum of the data values by the number of data values in the data set. For this data set, the mean can be calculated as 6 + 8 + 16 + 4 + 17 6 26 + 8 + 5 + 5 + 5 divided by 10, which is equivalent to 100/10 , or 10.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Problem
We are tasked with calculating the mean of the data set:
6, 8, 16, 4, 17, 26, 8, 5, 5, 5
The mean (or average) is calculated by summing up all the data values and dividing the sum by the total number of values in the data set.
Step 2: Write the Formula for the Mean
The formula for the mean is:
Mean = Sum of all data values/Number of data values.
Here, the number of data values is 10, since there are 10 numbers in the list.
Step 3: Find the Sum of All Data Values
Add up the numbers in the list:
6 + 8 + 16 + 4 + 17 + 26 + 8 + 5 + 5 + 5
Step-by-step calculation:
1) 6 + 8 = 14
2) 14 + 16 = 30
3) 30 + 4 = 34
4) 34 + 17 = 51
5) 51 + 26 = 77
6) 77 + 8 = 85
7) 85 + 5 = 90
8) 90 + 5 = 95
9) 95 + 5 = 100
So, the sum of all data values is 100.
Step 4: Divide the Sum by the Number of Data Values
Now divide the total sum by the number of values:
Mean = 100/10 = 10.
Step 5: Verify the Calculations
~ Recheck the sum: 6 + 8 + 16 + 4 + 17 + 26 + 8 + 5 + 5 + 5 = 100
~ Divide by 10: 100 ÷ 10 = 10.
The calculations are correct.
Final Answer: The mean of the data is: A) 10.
15th Question
Question: The equation E(t) = 5(1.8)t gives the estimated number of employees at a restaurant, where t is the number of years since the restaurant opened. Which of the following is the best interpretation of the number 5 in this context?
A) The estimated number of employees when the restaurant opened
B) The increase in the estimated number of employees each year
C) The number of years the restaurant has been open
D) The percent increase in the estimated number of employees each year
Choice A is correct. For an exponential function of the form E(t) = a(b)t, where a and b are constants, the initial value of the function—that is, the value of the function when t = 0 — is a and the value of the function increases by a factor of b each time t increases by 1. Since the function E(t) = 5(1.8)t gives the estimated number of employees at a restaurant and t is the number of years since the restaurant opened, the best interpretation of the number 5 in this context is the estimated number of employees when t = 0, or when the restaurant opened.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
Step 1: Understand the Problem
The given equation is:
E(t) = 5(1.8)t
~ E(t): Represents the estimated number of employees at the restaurant.
~ t: Represents the number of years since the restaurant opened.
~ 5: A constant that needs to be interpreted in the context of the problem.
We are tasked with interpreting the number 5 in this context.
Step 2: Analyze the Equation’s Components
This equation represents exponential growth because the variable t (time) is in the exponent. In the general form of an exponential function:
E(t) = a ⋅ (b)t
~ a: The initial value when t = 0.
~ b: The growth factor, where b > 1 indicates growth.
Here:
~ a = 5: This is the initial value of E(t), or the number of employees when t = 0.
~ b = 1.8: The growth factor, meaning the estimated number of employees increases by a factor of 1.8 each year.
Step 3: Interpret the Value of 5
~ When t = 0 (the restaurant has just opened):
E(0) = 5(1.8)0 = 5 ⋅ 1 = 5
This means there were 5 employees when the restaurant first opened.
Thus, 5 represents the initial number of employees at the time of opening.
Step 4: Evaluate the Answer Choices
A) The estimated number of employees when the restaurant opened:
This is correct because 5 is the initial value when t = 0.
B) The increase in the estimated number of employees each year:
This is incorrect because the number of employees grows exponentially, not linearly, and the growth is determined by the factor 1.8, not 5.
C) The number of years the restaurant has been open:
This is incorrect because t represents the number of years, not 5.
D) The percent increase in the estimated number of employees each year:
This is incorrect because the growth rate (in percentage terms) is determined by the factor 1.8, not 5. Specifically, the percentage increase is 80%, derived from (1.8 − 1) ⋅ 100 = 80%.
Final Answer: The correct interpretation is: Option A.
16th Question
y = 6x + 18
Question: One of the equations in a system of two linear equations is given. The system has no solution. Which equation could be the second equation in the system?
A) −6x + y = 18
B) −6x + y = 22
C) −12x + y = 36
D) −12x + y = 18
Choice B is correct. A system of two linear equations in two variables, x and y, has no solution if the lines represented by the equations in the xy-plane are parallel and distinct. Lines represented by equations in standard form, Ax + By = C and Dx + Ey = F, are parallel if the coefficients for x and y in one equation are proportional to the corresponding coefficients in the other equation, meaning D/A = E/B; and the lines are distinct if the constants are not proportional, meaning F/C is not equal to D/A or E/B. The given equation, y = 6x + 18, can be written in standard form by subtracting 6x from both sides of the equation to yield -6x + y = 18. Therefore, the given equation can be written in the form Ax + By = C, where A = -6, B = 1, and C = 18. The equation in choice B, -6x + y = 22, is written in the form Dx + Ey = F, where D = -6, E = 1, and F = 22. Therefore, D/A = -6/-6, which can be rewritten as D/A = 1; E/B = 1/1, which can be rewritten as E/B = 1; and F/C = 22/18, which can be rewritten as F/C = 11/9. Since D/A = 1, E/B = 1, and F/C is not equal to 1, it follows that the given equation and the equation -6x + y = 22 are parallel and distinct. Therefore, a system of two linear equations consisting of the given equation and the equation -6x + y = 22 has no solution. Thus, the equation in choice B could be the second equation in the system.
Choice A is incorrect. The equation -6x + y = 18 and the given equation represent the same line in the xy-plane. Therefore, a system of these linear equations would have infinitely many solutions, rather than no solution.
Choice C is incorrect. The equation -12x + y = 36 and the given equation represent lines in the xy-plane that are distinct and not parallel. Therefore, a system of these linear equations would have exactly one solution, rather than no solution.
Choice D is incorrect. The equation -12x + y = 18 and the given equation represent lines in the xy-plane that are distinct and not parallel. Therefore, a system of these linear equations would have exactly one solution, rather than no solution.
Step 1: Analyze the Given Equation
We are given the first equation in the system:
y = 6x + 18
This equation represents a straight line in slope-intercept form (y = mx + b), where:
~ The slope (m) is 6.
~ The y-intercept (b) is 18.
Step 2: Understanding When a System Has No Solution
A system of two linear equations has no solution if the lines represented by the equations are parallel but distinct.
Parallel lines have the same slope but different y-intercepts. Thus:
1) The second equation must have the same slope as 6x + 18, which is 6 or equivalent.
2) The second equation must have a different constant term (y-intercept).
Step 3: Rewrite Each Option in Slope-Intercept Form
Now, let’s rewrite the options in the form y = mx + b and compare slopes.
Option A: −6x + y = 18
Rearrange to slope-intercept form:
y = 6x + 18
~ The slope is 6, and the y-intercept is 18.
~ This is identical to the given equation, so the system would have infinitely many solutions, not no solution.
~ Option A is incorrect.
Option B: −6x + y = 22
Rearrange to slope-intercept form:
y = 6x + 22
~ The slope is 6, which is the same as the given equation (6x + 18).
~ The y-intercept is 22, which is different from 18.
~ Since the lines are parallel and distinct, the system has no solution.
~ Option B is correct.
Option C: −12x + y = 3
Rearrange to slope-intercept form:
y = 12x + 36
~ The slope is 12, which is different from 6.
~ Since the slopes are not the same, the lines are not parallel, and they will eventually intersect.
~ Option C is incorrect
Option D: −12x + y = 18
Rearrange to slope-intercept form:
y = 12x + 18
~ The slope is 12, which is different from 6.
~ Since the slopes are not the same, the lines are not parallel, and they will eventually intersect.
~ Option D is incorrect.
Step 4: Final Answer: The second equation that makes the system have no solution is: B)−6x + y = 22.
17th Question
Question: What is the area, in square centimeters, of a rectangle with a length of 34 centimeters (cm) and a width of 29 cm?
A) 846
B) 986
C) 1,176
D) 1,266
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 986. The area, A, of a rectangle is given by A = lw, where l is the length of the rectangle and w is its width. It’s given that the length of the rectangle is 34 centimeters (cm) and the width is 29 cm. Substituting 34 for l and 29 for w in the equation A = lw yields A = (34)(29), or A = 986. Therefore, the area, in square centimeters, of this rectangle is 986.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Formula for the Area of a Rectangle
The area A of a rectangle is calculated using the formula:
A = length × width
Where:
~ The length is the longer side of the rectangle.
~ The width is the shorter side of the rectangle.
Step 2: Identify the Given Values
From the problem:
~ Length = 34 cm
~ Width = 29 cm
Step 3: Substitute the Values into the Formula
Substitute the given length and width into the formula:
A = 34 × 29
Step 4: Perform the Multiplication
We calculate 34 × 29 step by step:
Break it into smaller parts (distributive property):
34 × 29 = 34 × (30 − 1) = (34 × 30) − (34 × 1)
Calculate each term:
1) 34 × 30 = 1020
2) 34 × 1 = 34
Subtract the results:
1020 − 34 = 986
Thus, the area of the rectangle is:
A = 986 square centimeters.
Final Answer: The area of the rectangle is: B) 986 cm2.
18th Question
y = 3x + 5
5y = 18x − 10
Question: The solution to the system is (x, y). What is the value of x − y?
A) 28.33
B) 18.24
C) 32.48
D) 48.44
Choice A is correct. The correct answer is 28.33.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Solve the System Using Substitution
We are given the first equation as y = 3x + 5. Using substitution, we replace y in the second equation with 3x + 5.
The second equation is:
5y = 18x − 10
Substitute y = 3x + 5 into 5y = 18x − 10:
5(3x + 5) = 18x − 10
Step 2: Simplify the Equation
Distribute the 5 on the left-hand side:
15x + 25 = 18x − 10
Rearrange the terms:
1) Move 18x to the left:
15x − 18x + 25 = −10
−3x + 25 = −10
2) Subtract 25 from both sides:
−3x = −35
3) Divide both sides by −3:
x = 35/3
Step 3: Find y

x – y = -85/3
x – y = 28.33.
Final Answer: A) 28.33.
19th Question
4x2 + 8x + 15 = 0
Question: How many distinct real solutions does the given equation have?
A) Zero
B) Exactly one
C) Exactly two
D) Infinitely many
Choice A is correct. There are Zero real solutions.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation:
The number of distinct real solutions of a quadratic equation depends on the discriminant (Δ) of the equation. For any quadratic equation in the form:
ax2 + bx + c = 0
The discriminant is given by:
Δ = b2 − 4ac
Step 1: Identify the coefficients a, b, and c
From the given equation 4x2 + 8x + 15 = 0:
a = 4, b = 8, c = 15
Step 2: Calculate the discriminant
Substitute the values of a, b, and c into the discriminant formula:
Δ = b2 − 4ac
Δ = (8)2 − 4(4)(15)
Δ = 64 − 240
Δ = −176
Step 3: Interpret the discriminant
The discriminant (Δ = −176) is negative, which means that the quadratic equation has no real solutions. Instead, it has two complex solutions.
Step 4: Choose the correct answer
The number of distinct real solutions is: Zero.
Verification:
To verify, the negative discriminant confirms the absence of real solutions. If Δ > 0, there would be two distinct real solutions. If Δ = 0, there would be exactly one real solution. A negative discriminant confirms that no real solutions exist.
Final Answer: A) Zero.
Why are there no real solutions?
The presence or absence of real solutions in a quadratic equation is determined by the discriminant (Δ), which is calculated using the formula:
Δ = b2 − 4ac
Here’s the key point:
1) If Δ > 0: There are two distinct real solutions.
2) If Δ = 0: There is exactly one real solution (a repeated root).
3) If Δ < 0: There are no real solutions, only complex (imaginary) solutions.
The sign of the discriminant determines whether the roots are real or imaginary.
20th Question
Question: A rectangular park has an area of 9,702,240 square yards. What is the area of the park, in square miles? (1 mile = 1,760 yards)
A) 1.4
B) 3.05
C) 3.13
D) 5.2
Choice C is correct. The real answer is 3.13.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Let’s start using the Desmos Calculator for easy calculation and better results.

Final Answer: C) 3.13.
21th Question
5x + 7y = 1
ax + by = 1
Question: In the given pair of equations, a and b are constants. The graph of this pair of equations in the xy-plane is a pair of perpendicular lines. Which of the following pairs of equations also represents a pair of perpendicular lines?
A) 10x + 7y = 1
ax – 2by = 1
B) 10x + 7y = 1
ax + 2by = 1
C) 10x + 7y = 1
2ax + by = 1
D) 5x − 7y = 1
ax + by = 1
Choice B is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
What Does “Perpendicular” Mean in Terms of Lines?
Two lines in the xy-plane are perpendicular if they meet at a 90-degree angle. Mathematically, for two lines to be perpendicular:
1) The product of their slopes (m1 and m2) must equal −1:
m1 ⋅ m2 = −1.
~ To find m1 or m2:
m1 = -1/m2
m2 = -1/m1
2) If one line has slope m1, the slope m2 of the perpendicular line is the negative reciprocal of m1. For example:
If m1 = 2, then m2 = −1/2.
If m1 = −3/4, then m2 = 4/3.
~ Expand it: m1 ⋅ m2 = −1.
-3/4 ⋅ m2 = −1
3/4 ⋅ m2 = 1
m2 = 4/3.

Verification of Options
Option A:
Equations:
10x + 7y = 1 and ax − 2by = 1.

We have got the answer, but still, there are more. Let’s check them too.

Final Answer: Option B.
22th Question
x2 – 34x + c = 0
Question: In the given equation, c is a constant. The equation has no real solutions if c > n. What is the least possible value of n?
A) 156
B) 345
C) 432
D) 289
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 289. A quadratic equation of the form ax2 + bx + c = 0, where a, b, and c are constants, has no real solutions when the value of the discriminant, b2 – 4ac, is less than 0. In the given equation, x2 – 34x + c = 0, a = 1 and b = -34. Therefore, the discriminant of the given equation can be expressed as (-34)2 -4(1), or 1,156 – 4c. It follows that the given equation has no real solutions when 1,156 – 4c < 0. Adding 4c to both sides of this inequality yields 1,156 < 4c. Dividing both sides of this inequality by 4 yields 289 < c, or c > 289. It’s given that the equation x2 – 34x + c = 0 has no real solutions when c > n. Therefore, the least possible value of n is 289.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Question Analysis
We are given the quadratic equation:
x2 − 34x + c = 0
Here, c is a constant, and the equation has no real solutions if c > n. We need to find the least possible value of n such that the quadratic equation has no real solutions.
For a quadratic equation ax2 + bx + c = 0, the discriminant (Δ) is used to determine the nature of the roots:
Δ = b2 − 4ac
~ If Δ > 0, the equation has two distinct real solutions.
~ If Δ = 0, the equation has one real solution (a repeated root).
~ If Δ < 0, the equation has no real solutions.
Thus, for the given quadratic equation to have no real solutions, we need: Δ < 0
Step-by-Step Solution
1. Write down the discriminant for the given equation:
The quadratic equation is:
x2 − 34x + c = 0
Here:
~ a = 1 (coefficient of x2),
~ b = −34 (coefficient of x),
~ c = c (constant term).
The discriminant is:
Δ = b2 − 4ac
Substitute the values of a and b:
Δ = (−34)2 − 4(1)(c)
Simplify:
Δ = 1156 − 4c
2. Set the condition for no real solutions:
The equation has no real solutions if: Δ < 0
Substitute Δ = 1156 − 4c:
1156 − 4c < 0
3. Solve for c:
Rearrange the inequality: 1156 < 4c
Divide both sides by 4: c > 289
Thus, the equation has no real solutions if c > 289.
4. Determine the least possible value of n:
The least possible value of n such that c > n ensures no real solutions is:
n = 289
Verification
1) If c = 289, the discriminant becomes:
Δ = 1156 − 4(289)
Δ = 1156 − 1156
Δ = 0
This means the equation has exactly one real solution, not no real solutions.
2) If c > 289, such as c = 290, the discriminant becomes:
Δ = 1156 − 4(290)
Δ =1156 − 1160
Δ = −4
Since Δ < 0, the equation has no real solutions.
Thus, n = 289 is correct.
Final Answer: D) 289.
Did you try all the features and get comfortable using them? You should work on using the Desmos calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must attempt as many questions as you can before the final test. This is the 7th Practice Test of SAT Math Module 2nd.
Either you can take the 8th Practice Test of SAT Math or the 8th Practice Test of SAT Reading and Writing Module 2nd.
- SAT Test 8th (Math Module 2nd)
- SAT Test 7th (Math Module 1st)
- SAT Test 7th (Reading and Writing Module 2nd)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


