
Prepare For The SATs: Math Test Module 1st with Simple Explanations, Tips and Tricks
Did you take the SAT Math Test 6 & 7? This is the 8th test. Like the other exams, it has the same format and all the necessary features for you to become a master in math. You take the SAT Test Module First to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after step-by-step explanations.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 1st.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 1ST
The first module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 1st are from easy to difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 1st. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH EQUATION SOLUTIONS WITH EXPLANATION AND TRICKS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
k + 12 = 336
Question: What is the solution to the given equation?
A) 28
B) 324
C) 348
D) 4,032
Choice B is correct. Subtracting 12 from both sides of the given equation yields k = 324. Therefore, the solution to the given equation is 324.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Equation
We are given the equation:
k + 12 = 336
Here, k is the unknown variable we need to solve for. The equation is a simple linear equation, meaning we can isolate k by performing basic arithmetic operations.
Step 2: Isolate k
To isolate k, subtract 12 from both sides of the equation. Subtraction is performed to undo the addition of 12 on the left-hand side.
k + 12 = 336
k = 336 − 12
Simplify:
k = 324
Step 3: Verify the Solution
To verify, substitute k = 324 back into the original equation:
k + 12 = 336
Substitute 324 for k:
324 + 12 = 336
Simplify:
336 = 336
This confirms that the solution k = 324 is correct.
Final Answer
The solution to the equation is: k = 324.
2nd Question
Question: The function f is defined by f(x) = x3 + 15. What is the value of f(2)?
A) 20
B) 21
C) 23
D) 24
Choice C is correct. The value of f(2) is the value of f(x) when x = 2. Substituting 2 for x in the given function yields f(2) = (2)3 + 15, or f(2) = 8 + 15, which is equivalent to f(2) = 23. Therefore, the value of f(2) is 23.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect. This is the value of f(2) when f(x) = x(3) + 15, rather than f(x) = x3 + 15.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the Function
The given function is:
f(x) = x3 + 15
This is a cubic function where the input x is raised to the power of 3, and then 15 is added to the result.
The task is to find the value of f(2), which means substituting x = 2 into the function.
Step 2: Substitute x = 2 into the Function
Replace x with 2 in the given function:
f(2) = 23 + 15
Step 3: Evaluate the Expression
1. Calculate 23:
23 = 2 × 2 × 2 = 8
2. Add 15 to 8:
f(2) = 8 + 15 = 23
Step 4: Verify the Calculation
To ensure correctness, recheck each step:
~ 23 = 8 is accurate.
~ 8 + 15 = 23 is also accurate.
Thus, the value of f(2) is confirmed as 23.
Final Answer: The value of f(2) is: 23.
3rd Question
Question: Sean rents a tent at a cost of $11 per day plus a one-time insurance fee of $10. Which equation represents the total cost c, in dollars, to rent the tent with insurance for d days?
A) c = 11(d + 10)
B) c = 10(d + 11)
C) c = 11d + 10
D) c = 10d + 11
Choice C is correct. It’s given that the cost of renting a tent is $11 per day for d days. Multiplying the rental cost by the number of days yields $11d, which represents the cost of renting the tent for d days before the insurance is added. Adding the one-time insurance fee of $10 to the rental cost of $11d gives the total cost c, in dollars, which can be represented by the equation c = 11d + 10.
Choice A is incorrect. This equation represents the total cost to rent the tent if the insurance fee was charged every day.
Choice B is incorrect. This equation represents the total cost to rent the tent if the daily fee was $(d + 11) for 10 days.
Choice D is incorrect. This equation represents the total cost to rent the tent if the daily fee was $10 and the one-time fee was $11.
Problem Breakdown
We are tasked with finding an equation to represent the total cost c, in dollars, for renting a tent. The given information includes:
~ A daily rental cost of $11 per day.
~ A one-time insurance fee of $10.
~ The number of days d that Sean rents the tent.
Step 1: Define the Variables
~ Daily rental cost: Renting the tent for d days will cost 11 × d, or 11d, dollars.
~ One-time insurance fee: This is a fixed amount of $10, regardless of the number of days rented.
~ Total cost c: The total cost is the sum of the daily rental cost and the insurance fee.
Step 2: Write the Equation
The total cost c can be represented by the equation:
c = 11d + 10
Step 3: Verify the Equation
Let’s test the equation with a couple of example values to ensure it represents the situation correctly.
1) If Sean rents the tent for 1 day (d = 1):
~ Daily cost: 11 × 1 = 11
~ Total cost: c = 11 + 10 = 21.
This matches expectations.
2) If Sean rents the tent for 5 days (d = 5):
~ Daily cost: 11 × 5 = 55
~ Total cost: c = 55 + 10 = 65.
Again, this is correct.
Step 4: Final Answer: The equation representing the total cost is:
c = 11d + 10.
4th Question
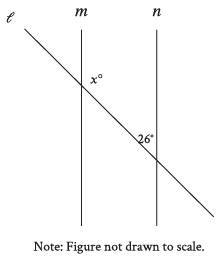
Question: In the figure shown, line m is parallel to line n. What is the value of x?
A) 13
B) 26
C) 52
D) 154
Choice D is correct. The sum of consecutive interior angles between two parallel lines and on the same side of the transversal is 180 degrees. Since it’s given that line m is parallel to line n, it follows that x + 26 = 180. Subtracting 26 from both sides of this equation yields 154. Therefore, the value of x is 154.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Breakdown
We are tasked with finding the value of x in the given figure. From the diagram, we know:
1) Line m is parallel to line n.
2) There is a transversal line, denoted as ℓ, intersecting lines m and n.
3) The angle adjacent to x∘ is 26∘.
Step 1: Understand the Parallel Lines and Transversal Properties
When a transversal intersects two parallel lines, several angle relationships are formed:
1) Corresponding angles are equal.
2) Alternate interior angles are equal.
3) Consecutive (same-side) interior angles are supplementary, meaning their sum is 180∘.
Step 2: Identify the Relevant Angles
In this case:
~ x∘ and 26∘ are consecutive interior angles because they are on the same side of the transversal ℓ and inside the parallel lines m and n.
~ By the consecutive interior angle property, we know:
x∘ + 26∘ = 180∘
Step 3: Solve for x
Using the equation:
x + 26 = 180
Subtract 26 from both sides:
x = 154
Thus, the value of x is: 154∘
Step 4: Verify the Solution
To verify:
~ x and 26∘ are consecutive interior angles, so their sum should equal 180∘.
~ Substituting x = 154 into the equation x + 26 = 180, we find:
154 + 26 = 180
This confirms that the solution is correct.
5th Question
Question: John paid a total of $165 for a microscope by making a down payment of $37 plus p monthly payments of $16 each. Which of the following equations represents this situation?
A) 16p − 37 = 165
B) 37p − 16 = 165
C) 16p + 37 = 165
D) 37p + 16 = 165
Choice C is correct. It’s given that John made a $16 payment each month for p months. The total amount of these payments can be represented by the expression 16p. The down payment can be added to that amount to find the total amount John paid, yielding the expression 16p + 37. It’s given that John paid a total of $165. Therefore, the expression for the total amount John paid can be set equal to that amount, yielding the equation 16p + 37 = 165.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown
We are tasked with finding an equation that represents the situation where John paid a total of $165 for a microscope. The payment structure includes:
1) A down payment of $37.
2) p monthly payments of $16 each.
We are to determine an equation that relates p, the number of monthly payments, to the total cost.
Step 1: Understand the Total Cost
The total cost of the microscope is given as:
Total Cost = Down Payment + Cost from Monthly Payments
The down payment is a fixed value of $37, and the cost from monthly payments is calculated as:
Cost from Monthly Payments = p ⋅ 16
Thus, the total cost can be expressed as:
165 = 37 + 16p
Step 2: Equation Setup
The equation representing the situation is:
165 = 37 + 16p
This equation expresses the relationship between the total cost 165, the down payment 37, and the monthly payments 16p.
Step 3: Verify the Equation
To verify, let’s solve the equation for p to ensure it makes sense. Subtract 37 from both sides:
165 − 37 = 16p
Simplify:
128 = 16p
Divide both sides by 16:
p = 8
So, John made 8 monthly payments, which checks out logically. Substituting p = 8 into the total cost:
165 = 37 + (16 ⋅ 8)
165 = 37 + 128
165 = 165
This confirms the equation is correct.
6th Question
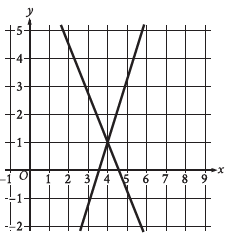
Question: The graph of a system of linear equations is shown. The solution to the system is (x, y). What is the value of x?
A) -1
B) -4
C) 1
D) 4
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Option D: The correct answer is 4. A solution to a system of equations must satisfy each equation in the system. It follows that if (x, y) is a solution to the system, the point (x, y) lies on the graph in the xy-plane of each equation in the system. According to the graph, the point (x, y) that lies on the graph of each equation in the system is (4, 1). Therefore, the solution to the system is (4, 1). It follows that the value of x is 4.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Analysis
The problem requires determining the x-coordinate of the intersection point of two lines represented by a system of linear equations, shown in the graph.
Step 1: Understand the Solution to a System of Linear Equations
The solution to a system of linear equations is the point where the two lines intersect. In this case, the graph shows two lines crossing at a specific point (x, y). The x-coordinate of this point is the desired solution.
Step 2: Read the Graph for the Intersection Point
From the graph:
~ Observe the point of intersection of the two lines.
~ The x-coordinate of the intersection point is directly read from the x-axis where the lines meet.
Looking closely at the graph, the lines intersect at:
(x, y) = (4, 0)
Thus, the value of x is:
x = 4
Step 3: Verify the Answer
To verify:
1) At x = 4, the two lines intersect, as shown clearly on the graph.
2) Substituting x = 4 into the equations of both lines (if provided) would yield the same y-coordinate, confirming the intersection.
Final Answer: The value of x is: 4.
7th Question
23, 27, 27, 32, 35, 36, 52
Question: What is the range of the 7 scores shown?
A) 25
B) 29
C) 39
D) 50
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B: The correct answer is 29. The range of a data set is the difference between its maximum value and its minimum value. For the data set shown, the maximum score is 52 and the minimum score is 23. The difference between those scores is 52 – 23, or 29. Therefore, the range of the 7 scores shown is 29.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis
The range of a data set is the difference between the largest and smallest values. It is a measure of how spread out the data is.
The given data set is:
23, 27, 27, 32, 35, 36, 52
We need to calculate the range of these 7 scores.
Step 1: Identify the Smallest and Largest Values
The smallest value in the data set is 23.
The largest value in the data set is 52.
Step 2: Apply the Formula for Range
The formula for the range is:
Range = Largest Value − Smallest Value
Substitute the values:
Range =52 − 23
Step 3: Perform the Calculation
Range = 29
Step 4: Verify the Answer
~ Double-check the smallest value (23) and largest value (52) in the data set to ensure no errors.
~ Perform the subtraction again: 52 − 23 = 29
The calculation is correct.
Final Answer: The range of the scores is: 29.
8th Question
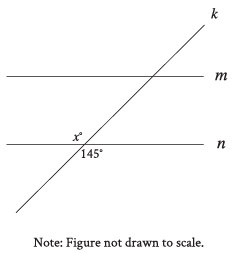
Question: In the figure, line m is parallel to line n, and line k intersects both lines. Which of the following statements is true?
A) The value of x is less than 145.
B) The value of x is greater than 145.
C) The value of x is equal to 145.
D) The value of x cannot be determined.
Choice C is correct. Vertical angles, or angles that are opposite each other when two lines intersect, are congruent. It’s given that line k intersects line n. Based on the figure, the angle with measure x° and the angle with measure 145° are vertical angles. Therefore, the value of x is equal to 145.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the absolute value of y, not the value of x .
Problem Statement:
We are analyzing the figure where:
1) m ∥ n (lines m and n are parallel).
2) k is a transversal.
3) The angle adjacent to x∘ is given as 145∘.
The goal is to determine the correct relationship for x based on the options.
Step 1: Relationship Between Angles
The angle x∘ and 145∘ are alternate interior angles because:
1) m ∥ n, and
2) k is a transversal intersecting the parallel lines.
Key property: Alternate interior angles are equal when lines are parallel.
Thus:
x = 145∘
Step 2: Verify the Options
Option Analysis:
A) The value of x is less than 145∘: FALSE.
x = 145, so this statement is incorrect.
B) The value of x is greater than 145∘: FALSE.
x = 145, so this statement is incorrect.
C) The value of x is equal to 145∘: TRUE.
This is correct because x = 145∘.
D) The value of x cannot be determined: FALSE.
Since m ∥ n, we can determine x = 145∘.
Final Answer: C) The value of x is equal to 145.
9th Question
Question: The equation x + y = 1,440 represents the number of minutes of daylight (between sunrise and sunset), x, and the number of minutes of non-daylight, y, on a particular day in Oak Park, Illinois. If this day has 670 minutes of daylight, how many minutes of non-daylight does it have?
A) 670
B) 770
C) 1,373
D) 1,440
Choice B is correct. It’s given that the equation x + y = 1,440 represents the number of minutes of daylight, x, and the number of minutes of non-daylight, y, on a particular day in Oak Park, Illinois. It’s also given that this day has 670 minutes of daylight. Substituting 670 for x in the equation x + y = 1,440 yields 670 + y = 1,440. Subtracting 670 from both sides of this equation yields y = 770. Therefore, this day has 770 minutes of non-daylight.
Choice A is incorrect. This is the number of minutes of daylight, not non-daylight, on this day.
Choice C is incorrect and may result from conceptual or calculation
errors.
Choice D is incorrect. This is the total number of minutes of daylight and non-daylight.
Problem Statement:
The equation x + y = 1440 represents the total number of minutes in a day.
~ x: number of minutes of daylight.
~ y: number of minutes of non-daylight.
We are given that x = 670 (minutes of daylight), and we need to find y (minutes of non-daylight).
Step 1: Understand the Total Minutes in a Day
A day has 1440 minutes in total (since there are 24 hours in a day and 24 × 60 = 1440).
The equation:
x + y = 1440
ensures that the sum of daylight (x) and non-daylight (y) minutes equals the total number of minutes in the day.
Step 2: Substitute x = 670 into the Equation
We are given x = 670. Substituting this value into the equation x + y = 1440, we get:
670 + y = 1440
Step 3: Solve for y
To find y, subtract 670 from both sides of the equation:
y = 1440 − 670
y = 770
Step 4: Verify the Solution
We verify the calculation:
x + y = 670 + 770 = 1440
The equation is satisfied, so the solution is correct.
Final Answer: The number of minutes of non-daylight is: 770 minutes.
10th Question
Question: Scott selected 20 employees at random from all 400 employees at a company. He found that 16 of the employees in this sample are enrolled in exactly three professional development courses this year. Based on Scott’s findings, which of the following is the best estimate of the number of employees at the company who are enrolled in exactly three professional development courses this year?
A) 4
B) 320
C) 380
D) 384
Choice B is correct. It’s given that from the sample of 20 employees at the company, 16 of the employees are enrolled in exactly three professional development courses this year. Since (16/20) is equal to 0.80, or 80/100, it follows that 80% of the employees in the sample are enrolled in exactly three professional development courses this year. Therefore, the best estimate for the percentage of employees at the company who are enrolled in exactly three professional development courses this year is 80%. It’s given that there are a total of 400 employees at the company. Therefore, the best estimate of the number of employees at the company who are enrolled in exactly three professional development courses this year is (80/100)(400), or 320.
Choice A is incorrect. This is the number of employees from the sample who aren’t enrolled in exactly three professional development courses this year.
Choice C is incorrect. This is the number of employees who weren’t selected for the sample.
Choice D is incorrect and may result from conceptual or calculation
errors.
Problem Statement:
Scott randomly selects 20 employees out of 400 employees. Among the sample, 16 employees are enrolled in exactly three professional development courses. Based on this sample, we are tasked to estimate how many employees, out of all 400, are enrolled in exactly three professional development courses.
Step 1: Understand Proportional Reasoning
The problem is based on the idea of proportionality. If p out of a sample of s employees have a certain characteristic, we can estimate the number N with that characteristic in the total population P using the proportion:

N = 320
Step 3: Verify the Solution
The proportion 16/20 simplifies to 0.8, meaning 80% of the sample is enrolled in 3 courses. Applying this percentage to the total population:
N = 0.8 ⋅ 400 = 320
The calculation matches, confirming the solution.
Final Answer: The best estimate of the number of employees enrolled in exactly three professional development courses is: 320.
11th Question
2.5b+5r= 80
Question: The given equation describes the relationship between the number of birds, b, and the number of reptiles, r, that can be cared for at a pet care business on a given day. If the business cares for 16 reptiles on a given day, how many birds can it care for on this day?
A) 0
B) 5
C) 40
D) 80
Choice A is correct. The number of birds can be found by calculating the value of b when r =16 in the given equation. Substituting 16 for r in the given equation yields 2.5b + 5(16) = 80, or 2.5b + 80 = 80. Subtracting 80 from both sides of this equation yields 2.5b = 0. Dividing both sides of this equation by 2.5 yields b = 0. Therefore, if the business cares for 16 reptiles on a given day, it can care for 0 birds on this day.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem:
The given equation is: 2.5b + 5r = 80
We are asked to find the number of birds, b, that the pet care business can care for on a day when r = 16 (number of reptiles).
Step-by-Step Solution:
Step 1: Substitute the value of r into the equation.
We are given that r = 16. Replace r with 16 in the equation:
2.5b + 5(16) = 80
Step 2: Simplify the equation.
First, calculate 5 × 16:
2.5b + 80 = 80
Step 3: Isolate 2.5b.
Subtract 80 from both sides:
2.5b = 0
Step 4: Solve for b.
Divide both sides by 2.5:
b = 0/2.5
b = 0
Verification:
If b = 0, substitute b and r = 16 back into the original equation:
2.5(0) + 5(16)
0 + 80 = 80
The calculation is correct.
Final Answer: The number of birds that can be cared for is 0.
12th Question
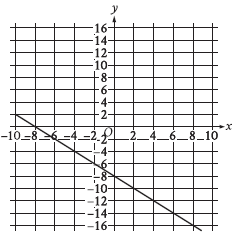
Question: What is an equation of the graph shown?
A) y = −2x − 8
B) y = x −8
C) y = −x − 8
D) y = 2x − 8
Choice C:

Choice A is incorrect. This is an equation of a line with a slope of -2, not -1.
Choice C is incorrect. This is an equation of a line with a slope of 1, not -1.
Choice D is incorrect. This is an equation of a line with a slope of 2, not -1.
Problem:
We are tasked with determining the equation of the line shown in the graph. The line passes through the points (0, −8) and (−8, 0).
Step-by-Step Solution:
Step 1: Recall the slope-intercept form of a linear equation.
The slope-intercept form of a linear equation is:
y = mx + b
where:
m is the slope of the line.
b is the y-intercept, the value of y when x = 0.
Step 2: Identify the y-intercept (b).

Step 4: Write the equation.
Substitute m = −1 and b = −8 into the slope-intercept form:
y = −x − 8
Step 5: Verify the equation.
To confirm, substitute the coordinates of the given points into the equation y = −x − 8:
1) For x = 0:
y = −(0) − 8 = −8
Correct.
2) For x = −8:
y = −(−8) − 8
y = 8 − 8
y = 0
Correct.
The equation matches the graph.
Final Answer: The equation of the graph is: C) y = −x − 8.
13th Question
Question: If x/8 = 5, what is the value of 8/x?
A) 1/3
B) 1/4
C) 1/5
D) 1/8
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice C is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem:
We are given the equation:
x/8 = 5
We are tasked with finding the value of 8/x.
Step-by-Step Solution:
Step 1: Solve for x from the given equation.
The given equation is:
x/8 = 5
To isolate x, multiply both sides of the equation by 8:
x = 8 ⋅ 5 = 40
So, x = 40.
Step 2: Substitute x = 40 into 8/x.

Final Answer: The value of 8/x is: C) 1/5.
14th Question
24x + y = 48
6x + y = 72
Question: The solution to the given system of equations is (x, y). What is the value of y?
A) 72
B) 30
C) 80
D) 48
Choice C is correct. The correct answer is 80. Subtracting the second equation in the given system from the first equation yields (24x + y) – (6x + y) = 48 – 72, which is equivalent to 24x – 6x + y – y = -24, or 18x = -24. Dividing each side of this equation by 3 yields 6x = -8. Substituting -8 for 6x in the second equation yields -8 + y = 72. Adding 8 to both sides of this equation yields y = 80.
Alternate approach: Multiplying each side of the second equation in the given system by 4 yields 24x + 4y = 288. Subtracting the first equation in the given system from this equation yields (24x + 4y) – (24x + y) = 288 – 48, which is equivalent to 24x – 24x + 4y – y = 240, or 3y = 240. Dividing each side of this equation by 3 yields y = 80.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem:
We are tasked with solving the system of equations:
1) 24x + y = 48
2) 6x + y = 72
The goal is to find the value of y.
Step-by-Step Solution:
Step 1: Label the equations.
Let:
~ 24x + y = 48 be Equation (1)
~ 6x + y = 72 be Equation (2)
Step 2: Eliminate y by subtraction.
To eliminate y, subtract Equation (2) from Equation (1):
(24x + y) − (6x + y) = 48 − 72
Simplify:
24x − 6x + y − y = −24
18x = −24

Final Answer: The value of y is: 80.
15th Question
Question: Line t in the xy-plane has a slope of – 1/3 and passes through the point (9, 10). Which equation defines line t?
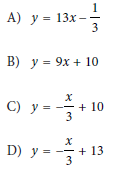
Choice D
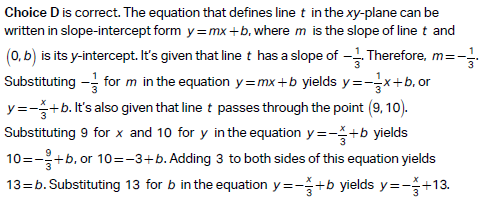
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect. This equation defines a line that has a slope of 9, not -1/3, and passes through the point (0, 10), not (9, 10).
Choice C is incorrect. This equation defines a line that passes through the point (0, 10), not (9, 10).
Step-by-Step Solution:
Step 1: Recall the point-slope formula.
The point-slope formula for the equation of a line is:
y − y1 = m(x − x1)
Where:
~ m is the slope,
~ (x1, y1) is a point on the line.
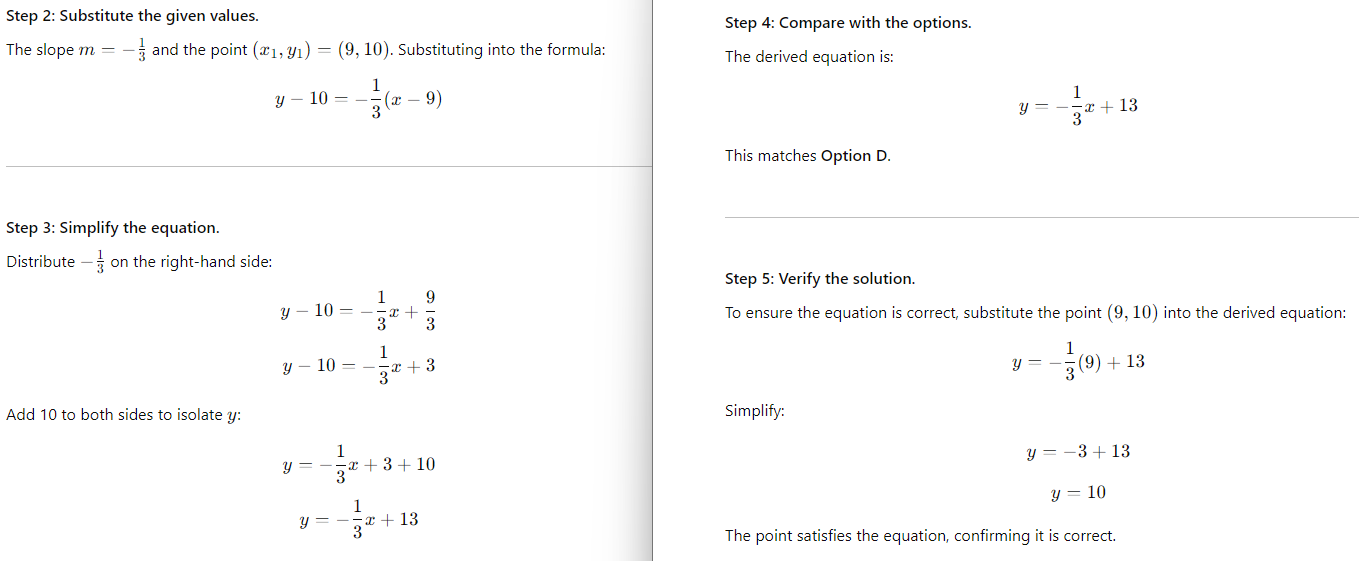
Final Answer: The correct equation is: Option D.
16th Question
Question: Circle A has a radius of 3n and circle B has a radius of 129n, where n is a positive constant. The area of circle B is how many times the area of circle A?
A) 43
B) 86
C) 129
D) 1,849
Choice D is correct. The area of a circle can be found by using the formula A = πr2, where A is the area and r is the radius of the circle. It’s given that the radius of circle A is 3n. Substituting this value for r into the formula A = πr2 gives A = π(3n)2, or 9πn2. It’s also given that the radius of circle B is 129n. Substituting this value for r into the formula A = πr2 gives A = π(129n)2, or 16,641πn2. Dividing the area of circle B by the area of circle A gives 16,641πn2/9πn2, which simplifies to 1,849. Therefore, the area of circle B is 1,849 times the area of circle A.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem:
We are tasked with determining how many times the area of Circle B is compared to Circle A. The radii of the circles are given as:
~ Circle A: Radius = 3n
~ Circle B: Radius = 129n
Where n is a positive constant.
Step-by-Step Solution:
Step 1: Recall the formula for the area of a circle.
The area of a circle is given by:
Area = πr2
Where r is the radius of the circle.
Step 2: Calculate the area of Circle A.
For Circle A, the radius is 3n:
Area of Circle A = π(3n)2
Simplify:
Area of Circle A = π(9n2)
Area of Circle A = 9πn2
Step 3: Calculate the area of Circle B.
For Circle B, the radius is 129n:
Area of Circle B = π(129n)2
Simplify:

Step 5: Verify the solution.
Both calculations for the areas and the ratio involve standard operations, and the simplification checks out.
Final Answer: The area of Circle B is 1,849 times the area of Circle A.
17th Question
| Data Value | Frequency |
|---|---|
| 6 | 3 |
| 7 | 3 |
| 8 | 8 |
| 9 | 8 |
| 10 | 9 |
| 11 | 11 |
| 12 | 9 |
| 13 | 0 |
| 14 | 6 |
Question: The frequency table summarizes the 57 data values in a data set. What is the maximum data value in the data set?
A) 9
B) 11
C) 14
D) 18
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice C: The correct answer is 14. The maximum value is the largest value in the data set. The frequency refers to the number of times a data value occurs. The given frequency table shows that for this data set, the data value 6 occurs three times, the data value 7 occurs three times, the data value 8 occurs eight times, the data value 9 occurs eight times, the data value 10 occurs nine times, the data value 11 occurs eleven times, the data value 12 occurs nine times, the data value
13 occurs zero times, and the data value 14 occurs six times. Therefore, the maximum data value in the data set is 14.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem:
In the frequency table:
From this table:
~ x represents the possible data values in the data set.
~ f represents how many times each x occurs in the data set.
Data Value (x): 6, 7, 8, 9, 10, 11, 12, 13, 14
Frequency (f): 3, 3, 8, 8, 9, 11, 9, 0, 6
f is the frequency, or the number of times each data value x appears in the data set.
For example:
1) x = 6: appears 3 times (f = 3).
2) x = 7: appears 3 times (f = 3).
3) x = 8: appears 8 times (f = 8).
And so on.
To find the total number of data values, we sum all the frequencies (f) in the table.
Step-by-Step Calculation of Total Data Values:
Total Data Values = ∑f
Add the frequencies for all x:
f = 3 + 3 + 8 + 8 + 9 + 11 + 9 + 0 + 6
Perform the addition step by step:
3 + 3 = 6
6 + 8 = 14
14 + 8 = 22
22 + 9 = 31
31 + 11 = 42
42 + 9 = 51
51 + 0 = 51
51 + 6 = 57
Thus, the total number of data values is: 57.
Why is 57 important?
~ The total 57 confirms that the table summarizes all the data values in the data set.
~ The frequencies (f) tell us how many times each specific data value appears. Without f, we would only have a list of potential data values, not the count of their occurrences.
The total number of data values is ∑f = 57, as given.
Step-by-Step Solution:
Step 1: Understand the meaning of “maximum data value.”
The maximum data value is the largest x for which f > 0. This means we need to find the largest x in the table where the frequency is not zero.
Step 2: Locate the maximum data value.
~ The largest data value in the table is x = 14.
~ The corresponding frequency for x = 14 is f = 6, which is greater than 0.
Since x = 14 has a positive frequency, it is part of the data set and is therefore the maximum data value.
Step 3: Verify the solution.
The frequency of x = 14 confirms that this value appears 6 times in the data set, making it valid. All larger x values are not present in the table, so x = 14 is indeed the maximum.
Final Answer: The maximum data value in the data set is 14.
18th Question
Question: For the function q, the value of q(x) decreases by 45% for every increase in the value of x by 1. If q(0) = 14, which equation defines q?
A) q(x) = 0.55(14)x
B) q(x) = 1.45(14 )x
C) q(x) = 14(0.55)x
D) q(x) = 14(1.45)x
Choice C:

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. For this function, the value of q(x) increases, rather than decreases, by 45% for every increase in the value of x by 1.
Problem Breakdown:
We are tasked with identifying the equation that defines the function q(x), where the value of q(x) decreases by 45% for every increase in x by 1. Additionally, we know that q(0) = 14. Let’s solve step-by-step to understand and verify the correct equation.
Step 1: Understanding the exponential decay formula
When a quantity decreases by a fixed percentage for each unit of increase in x, it follows an exponential decay formula:
q(x) = q0 ⋅ rx
~ q(x): The value of the function at x.
~ q0: The initial value of the function (q(0)).
~ r: The decay factor, representing how much of the original value remains after each increase in x by 1.
~ x: The independent variable.
Step 2: Identifying the components
1) Initial value:
~ From the problem, q(0) = 14. So, q0 = 14.
2) Decay factor:
~ The function decreases by 45% for every increase in x by 1.
~ If a quantity decreases by 45%, the remaining percentage is:
100% − 45% = 55%
~ In decimal form, the decay factor is: r = 0.55
Step 3: Substituting into the formula
Using the formula q(x) = q0 ⋅ rx, we substitute q0 = 14 and r = 0.55:
q(x) = 14 ⋅ (0.55)x
Step 4: Match with the given options
The correct equation is:
q(x) = 14(0.55)x
This corresponds to Option C.
Step 5: Verification
Let’s verify the equation by calculating some values for q(x) and ensuring the 45% decrease is reflected:
1) Initial value q(0):
q(0) = 14 ⋅ (0.55)0
q(0) = 14 ⋅ 1 = 14
This matches the given q(0) = 14.
2) For q(1):
q(1) = 14 ⋅ (0.55)1
q(1) =14 ⋅ 0.55 = 7.7
The value decreases from 14 to 7.7, which is a 45% decrease:
14 ⋅ 0.45 = 6.3 and 14 − 6.3 = 7.7
3) For q(2):
q(2) = 14 ⋅ (0.55)2
q(2) = 14 ⋅ 0.3025 = 4.235
The value decreases by 45% again from 7.7 to 4.235.
This confirms the function correctly represents the decay.
19th Question
Question:
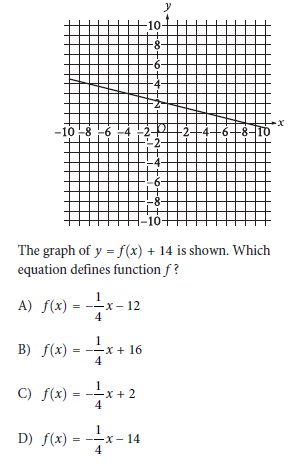
Choice A:

Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Find the slope of the line
The points are:
~ Point 1: (0, 2)
~ Point 2: (4, 1)
The slope formula is:

b = 2
Thus, the equation of y = f(x) + 14 is:
y = – 1/4x + 2

Final Answer: Option A.
20th Question
RS = 20
ST = 48
TR = 52
Question: The side lengths of right triangle RST are given. Triangle RST is similar to triangle UVW, where S corresponds to V and T corresponds to W. What is the value of tan W?
A) 5/13
B) 5/12
C) 12/13
D) 12/5
Choice B is correct. It’s given that right triangle RST is similar to triangle UVW, where S corresponds to V and T corresponds to W. It’s given that the side lengths of the right triangle RST are RS = 20, ST = 48, and TR = 52. Corresponding angles in similar triangles are equal. It follows that the measure of angle T is equal to the measure of angle W. The hypotenuse of a right triangle is the longest side. It follows that the hypotenuse of triangle RST is side TR. The hypotenuse of a right triangle is the side opposite the right angle. Therefore, angle S is a right angle. The adjacent side of an acute angle in a right triangle is the side closest to the angle that is not the hypotenuse. It follows that the adjacent side of angle T is side ST. The opposite side of an acute angle in a right triangle is the side across from the acute angle. It follows that the opposite side of angle T is side RS. The tangent of an acute angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side. Therefore, tan T = RS/ST. Substituting 20 for RS and 48 for ST in this equation yields tan T = 20/48, or T = 5/12. The tangents of two acute angles with equal measures are equal. Since the measure of angle T is equal to the measure of angle W, it follows that tan T = tanW. Substituting 5/12 for tan T in this equation yields 5/12 = tan W. Therefore, the value of tan W is 5/12.
Choice A is incorrect. This is the value of sin W.
Choice C is incorrect. This is the value of cos W.
Choice D is incorrect. This is the value of 1/tan W.
Step 1: Understand the given information
Triangle RST is a right triangle with side lengths:
~ RS = 20 (one leg)
~ ST = 48 (another leg)
~ TR = 52 (the hypotenuse)
~ Triangle RST is similar to triangle UVW, and S corresponds to V, and T corresponds to W.
~ We are tasked with finding tanW.
Step 2: Verify if the given triangle is a right triangle
To verify that RST is a right triangle, check if the Pythagorean theorem holds:
a2 + b2 = c2
Substitute the side lengths:
202 + 482 = 522
Calculate each term:
202 = 400, 482 = 2304, 522 = 2704
400 + 2304 = 2704
Since the equation holds, the triangle is indeed a right triangle.
Step 3: Recall the definition of tan

Step 5: Match with the answer choices
The value of tanW = 5/12, which corresponds to: B) 5/12.
Step 6: Verification
Since triangle RST is similar to triangle UVW, the corresponding angles have the same tangent values. Thus, the calculation for tanT is valid for tanW.
21th Question
Question: One gallon of paint will cover 220 square feet of a surface. A room has a total wall area of w square feet. Which equation represents the total amount of paint P, in gallons, needed to paint the walls of the room twice?
A) P = w/110
B) P = 440w
C) P = w/220
D) P = 220w
Choice A is correct. It’s given that w represents the total wall area, in square feet. Since the walls of the room will be painted twice, the amount of paint, in gallons, needs to cover 2w square feet. It’s also given that one gallon of paint will cover 220 square feet. Dividing the total area, in square feet, of the surface to be painted by the number of square feet covered by one gallon of paint gives the number of gallons of paint that will be needed. Dividing 2w by 220 yields 2w/220, or w/110. Therefore, the equation that represents the total amount of paint P, in gallons, needed to paint the walls of the room twice is P = w/110.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from finding the amount of paint needed to paint the walls once rather than twice.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation
The problem asks for the total amount of paint P, in gallons, required to paint a room with total wall area w square feet twice, given that 1 gallon of paint covers 220 square feet.
Step 1: Understand the relationship
~ Total area to be painted: Since the walls need to be painted twice, the total area to be covered is 2w (twice the wall area w).
~ Paint coverage per gallon: 1 gallon of paint covers 220 square feet.
To find the total amount of paint required, divide the total area to be painted by the paint coverage per gallon.

Step 4: Verify the equation
Let’s test the equation with an example:
~ Suppose the total wall area w = 220 square feet. Painting the walls twice gives a total area of 2 × 220 = 440 square feet.
~ Since 1 gallon covers 220 square feet, the total paint required is 440 ÷ 220 = 2 gallons.
~ Using the equation P = w/110:
P = 220/110 = 2
The equation works correctly.
22th Question
Question: The number a is 110% greater than the number b. The number b is 90% less than 47. What is the value of a?
A) 9.87
B) 1.1
C) 1.47
D) 9.47
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 9.87. It’s given that the number a is 110% greater than the number b. It follows that a = (1 + 110/100)b, or a = 2.1b. It’s also given that the number b is 90% less than 47. It follows that b = (1 – 90/100)(47), or b = 0.1(47), which yields b = 4.7. Substituting 4.7 for b in the equation a = 2.1b yields a = 2.1(4.7), which is equivalent to a = 9.87. Therefore, the value of a is 9.87.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
We are tasked to find the value of a, given the relationships between a and b, and the value of b is based on 90% less than 47.
Step 1: Break down the problem
1) Relationship between b and 47:
~ b is 90% less than 47.
~ To calculate this, subtract 90% of 47 from 47:
b = 47 − (0.9 × 47)
2) Relationship between a and b:
~ a is 110% greater than b.
~ To calculate this, multiply b by 1 + 1.1 (since 110% greater is equivalent to 210% or 2.1 × b)
a = 2.1 × b
Step 2: Solve for b
Substitute the given information:
b = 47 − (0.9 × 47)
Calculate:
0.9 × 47 = 42.3
b = 47 − 42.3
Thus: b = 4.7
Step 3: Solve for a
Using the relationship a = 2.1 × b, substitute b = 4.7:
a = 2.1 × 4.7
Perform the multiplication:
a = 9.87
Final Answer: The value of a is: 9.87.
Step 4: Verify the Solution
~ Check b = 47 − 42.3 = 4.7, so b is correct.
~ Check a = 2.1 × 4.7 = 9.87, so a is correct.
Did you try all the features and get comfortable using them? You should work on using the calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must try to work on your speed and spend less time on the beginning and more on the later questions. This is the 8th Practice Test of SAT Math Module 1st.
Either you can take the 1st Practice Test of SAT Math or the 8th Practice Test of SAT Math Module 2nd.
- SAT Test 8th (Math Module 2nd)
- SAT Test 1st (Math Module 1st)
- SAT Test 8th (Reading and Writing Module 1st)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


