
Prepare For The SATs: Math Test Module 2nd with Simple Explanations, Tips and Tricks
Have you taken the module 1st? If yes, then you are in the right place. This is the 8th Test of Module 2nd. We have designed a similar exam format with all the necessary features for you to become a master in Math. You take the SAT Test Module Second to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 2nd.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 2ND
The second module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 2nd are only difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 2nd. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH STUDY GUIDE AND PROBLEM SOLUTIONS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: Isabel grows potatoes in her garden. This year, she harvested 760 potatoes and saved 10% of them to plant next year. How many of the harvested potatoes did Isabel save to plant next year?
A) 66
B) 76
C) 84
D) 86
Choice B is correct. The number of harvested potatoes Isabel saved to plant next year can be calculated by multiplying the total number of potatoes Isabel harvested, 760, by the proportion of potatoes she saved. Since she saved 10% of the potatoes she harvested, the proportion of potatoes she saved is 10/100, or 0.1. Multiplying 760 by this proportion gives 760(0.1), or 76, potatoes that she saved to plant next year.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Question Analysis
Isabel harvested a total of 760 potatoes and decided to save 10% of them to plant next year. We need to calculate how many potatoes Isabel saved.
This is a percentage problem where we calculate a given percentage of a total amount.
Step-by-Step Solution
1. Understand the percentage formula:
The formula to calculate a percentage of a number is:
Percentage value = (Percentage/100) × Total
Here:
Percentage = 10%
Total = 760 potatoes
Substituting these values into the formula:
Percentage value = (10/100) × 760
2. Simplify the percentage:
10/100 = 0.1
Now substitute:
Percentage value = 0.1 × 760
3. Perform the multiplication:
0.1 × 760 = 760.
4. Interpret the result:
Isabel saved 76 potatoes to plant next year.
Verification
Let’s verify the calculation:
10% of 760 = 10/100 × 760 = 76, which matches our result.
Final Answer: B) Isabel saved 76 potatoes.
2nd Question
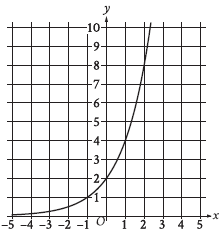
Question: What is the y-intercept of the graph shown?
A) (0, 0)
B) (0, 2)
C) (2, 0)
D) (2, 2)
Choice B is correct. The y-intercept of a graph in the xy-plane is the point at which the graph crosses the y-axis. The graph shown crosses the y-axis at the point (0, 2). Therefore, the y-intercept of the graph shown is (0, 2).
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Question Analysis
The question asks for the y-intercept of the graph shown. The y-intercept is the point where the graph crosses the y-axis (where x = 0).
Step-by-Step Solution
1. Understand the concept of the y-intercept:
~ The y-intercept is the value of y when x = 0.
~ To find this value, we locate the point on the graph where the x-coordinate is 0.
2. Analyze the graph:
~ Observe the graph provided. Look at the point where the curve intersects the y-axis.
~ From the graph:
~ ~ The curve crosses the y-axis at y = 2.
~ ~ Therefore, the y-intercept is (0, 2).
3. Verify the result:
~ Check the graph again to confirm that when x = 0, y = 2.
~ This matches the given y-intercept (0, 2).
Final Answer: The y-intercept of the graph is: B) (0, 2).
3rd Question
Question: What length, in centimeters, is equivalent to a length of 51 meters? (1 meter = 100 centimeters)
A) 0.051
B) 0.51
C) 5,100
D) 51,000
Choice C is correct. Since 1 meter is equal to 100 centimeters, 51 meters is equal to (100 centimeters/1 meter), or 5,100 centimeters.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from dividing, rather than multiplying, 51 by 100.
Choice D is incorrect. This is the length, in millimeters rather than centimeters, that is equivalent to a length of 51 meters.
Question Analysis
The question asks to convert a length given in meters (51 meters) to centimeters, using the relationship:
1 meter = 100 centimeters.
This is a straightforward unit conversion problem that involves multiplication.
Step-by-Step Solution
1. Understand the conversion factor:
~ The problem states that 1 meter = 100 centimeters.
~ To convert meters to centimeters, multiply the number of meters by 100.
2. Set up the calculation:
~ The given length is 51 meters.
~ Multiply 51 by the conversion factor of 100:
51 × 100 = 5100 centimeters.
3. Verify the calculation:
~ Double-check the multiplication: 51 × 100 = 5100 centimeters.
The calculation is correct.
Final Answer: The length of 51 meters is equivalent to: C) 5100 centimeters.
4th Question
4x + 5 = 165
Question: What is the solution to the given equation?
A) 40
B) 60
C) 145
D) 160
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 40. Subtracting 5 from both sides of the given equation yields 4x = 160. Dividing both sides of this equation by 4 yields x = 40. Therefore, the solution to the given equation is 40.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Question Analysis
The given equation is:
4x + 5 = 165
The question asks us to solve for x. This involves isolating x on one side of the equation using basic algebraic operations.
Step-by-Step Solution
1. Isolate the term with x:
To isolate 4x, subtract 5 from both sides of the equation:
4x + 5 − 5 = 165 − 5
4x = 160
2. Solve for x:
Divide both sides of the equation by 4 to find x:
4x/4 = 160/4
x = 40
3. Verify the solution:
Substitute x = 40 back into the original equation to ensure it satisfies the equation:
4(40) + 5 = 165
160 + 5 = 165
165 = 165
The solution is correct.
Final Answer: The solution to the equation is: A) 40.
5th Question
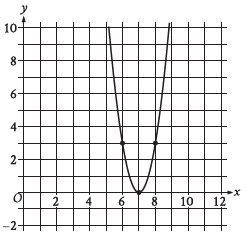
Question: The x-intercept of the graph shown is (x, 0). What is the value of x?
A) 6
B) 7
C) 8
D) 9
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 7. It’s given that the x-intercept of the graph shown is (x, 0). The graph passes through the point (7, 0). Therefore, the value of x is 7.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Learn to use the Desmos Calculator and there is a graph also available.
The question tells us that (x, 0), it shows we know y = 0. So, what is x then?
Observe the graph:
~ In the x-axis, there is a digit gap between values like 2, 4, 6, 8.
~ When the y-axis is 0 that time there is a point in the x-axis, which is between 6 and 8, so it is 7 for sure.
Final Answer: B) 7.
6th Question
Question: A moving truck can tow a trailer if the combined weight of the trailer and the boxes it contains is no more than 4,600 pounds. What is the maximum number of boxes this truck can tow in a trailer with a weight of 500 pounds if each box weighs 120 pounds?
A) 34
B) 35
C) 38
D) 39
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. It’s given that the truck can tow a trailer if the combined weight of the trailer and the boxes it contains is no more than 4,600 pounds. If the trailer has a weight of 500 pounds and each box weighs 120 pounds, the expression 500 + 120b, where b is the number of boxes, gives the combined weight of the trailer and the boxes. Since the combined weight must be no more than 4,600 pounds, the possible numbers of boxes the truck can tow are given by the inequality 500 + 120b < 4,600. Subtracting 500 from both sides of this inequality yields 120b < 4,100. Dividing both sides of this inequality by 120 yields b < 205/6, or b is less than or equal to approximately 34.17. Since the number of boxes, b, must be a whole number, the maximum number of boxes the truck can tow is the greatest whole number less than 34.17, which is 34.
Choice B is incorrect. Towing the trailer and 35 boxes would yield a combined weight of 4,700 pounds, which is greater than 4,600 pounds.
Choice C is incorrect. Towing the trailer and 38 boxes would yield a combined weight of 5,060 pounds, which is greater than 4,600 pounds.
Choice D is incorrect. Towing the trailer and 39 boxes would yield a combined weight of 5,180 pounds, which is greater than 4,600 pounds.
Problem Breakdown
We are tasked with finding the maximum number of boxes a moving truck can tow under the following conditions:
1) The combined weight of the trailer and the boxes it contains must be no more than 4,600 pounds.
2) The trailer weighs 500 pounds on its own.
3) Each box weighs 120 pounds.
Step-by-Step Solution
1. Understanding the Problem
The truck’s total towing limit is 4,600 pounds. This includes:
~ The weight of the trailer: 500 pounds.
~ The weight of the boxes: 120 pounds per box.
Let x represent the number of boxes. The total weight of the trailer and boxes is:
Total Weight = Weight of Trailer + Weight of Boxes
This must satisfy the condition:
500 + 120x ≤ 4,600
2. Set Up the Inequality
Substitute the weights into the inequality:
500 + 120x ≤ 4,600
3. Solve for x
To isolate x, subtract 500 from both sides:
120x ≤ 4,600 − 500
120x ≤ 4,100
Now, divide both sides by 120 to solve for x:
x ≤ 4,100/120
Perform the division:
x ≤ 34.17
4. Interpret the Result
Since x represents the number of boxes, it must be a whole number. The largest integer less than or equal to 34.16 is:
x = 34
Thus, the maximum number of boxes the truck can tow is 34.
Step-by-Step Verification
1) Calculate the total weight for x = 34:
Total Weight = 500 + 120(34)
= 500 + 4,080
= 4,580 pounds.
This is less than 4,600 pounds, so x = 34 works.
2) Check for x = 35:
Total Weight = 500 + 120(35)
= 500 + 4,200
= 4,700 pounds.
This exceeds 4,600 pounds, so x = 35 is not valid.
Final Answer: The maximum number of boxes the truck can tow is: A) 34.
7th Question
-4x2 – 7x = -36
Question: What is the positive solution to the given equation?
A) 7/4
B) 9/4
C) 4
D) 7
Choice B is correct. Multiplying each side of the given equation by -16 yields 64x2 + 112x = 576. To complete the square, adding 49 to each side of this equation yields 64x2 + 112x + 49 = 576 + 49, or (8x + 7)2 = 625. Taking the square root of each side of this equation yields two equations: 8x + 7 = 25 and 8x + 7 = -25. Subtracting 7 from each side of the equation 8x + 7 = 25 yields 8x = 18. Dividing each side of this equation by 8 yields x = 18/8, or x = 9/4. Therefore, 9/4 is a solution to the given equation. Subtracting 7 from each side of the equation 8x + 7 = -25 yields 8x = -32. Dividing each side of this equation by 8 yields x = -4. Therefore, the given equation has two solutions, 9/4 and -4. Since 9/4 is positive, it follows that 9/4 is the positive solution to the given equation.
Alternate approach: Adding 4x2 and 7x to each side of the given equation yields 0 = 4x2 + 7x – 36. The right-hand side of this equation can be rewritten as 4x2 + 16x – 9x – 36. Factoring out the common factor of 4x from the first two terms of this expression and the common factor of -9 from the second two terms yields 4x(x + 4) – 9(x + 4). Factoring out the common factor of (x + 4) from these two terms yields the expression (4x – 9)(x + 4). Since this expression is equal to 0, it follows that either 4x – 9 = 0 or x + 4 = 0. Adding 9 to each side of the equation 4x – 9 = 0 yields 4x = 9. Dividing each side of this equation by 4 yields x = 9/4. Therefore, 9/4 is a positive solution to the given equation. Subtracting 4 from each side of the equation x + 4 = 0 yields x = -4. Therefore, the given equation has two solutions, 9/4 and -4. Since 9/4 is positive, it follows that 9/4 is the positive solution to the given equation.
Choice A is incorrect. Substituting 7/4 for x in the given equation yields -49/2 = -36, which is false.
Choice C is incorrect. Substituting 4 for x in the given equation yields -92 = -36, which is false.
Choice D is incorrect. Substituting 7 for x in the given equation yields -245 = -36, which is false.
We are tasked with solving the quadratic equation −4x2 − 7x = −36 for its positive solution. Let’s approach this using two methods:
(1) Factoring Formula
(2) Quadratic Formula.
Step 1: Rewrite the Equation
Start by rearranging the equation into standard quadratic form
−4x2 − 7x + 36 = 0
Now, divide the entire equation by −1 (to simplify):
4x2 + 7x − 36 = 0
We will now solve this equation for x.
Method 1: Factoring
1) Identify coefficients: From 4x2 + 7x − 36 = 0, we have:
~ a = 4 (coefficient of x2),
~ b = 7 (coefficient of x),
~ c = −36 (constant term).
2) Multiply a and c: Multiply the leading coefficient (a = 4) and the constant term (c = −36):
a × c = 4 × (−36) = −144
3) Find two numbers that multiply to −144 and add to b = 7: The two numbers are 16 and -9, because:
16 × (−9) = −144 and 16 + (−9) = 7
4) Split the middle term 7x using 16x and −9x: Rewrite the quadratic equation as:
4x2 + 16x − 9x − 36 = 0
5) Group terms and factor each group: Group the terms into two pairs:
(4x2 + 16x) − (9x + 36) = 0
Factor out the greatest common factor (GCF) from each group:
4x(x + 4) − 9(x + 4) = 0
6) Factor the common binomial:
(4x− 9)(x + 4) = 0
7) Solve for x: Set each factor equal to 0:
4x − 9 = 0 or x + 4 = 0
Solve each equation:
4x = 9 ⇒ x = 9/4
x + 4 = 0 ⇒ x = −4
8) Choose the positive solution: Since we are asked for the positive solution:
x = 9/4
Method 2: Quadratic Formula
The quadratic formula is:

7) Choose the positive solution: Since we are asked for the positive solution: x = 9/4
Final Answer: B) 9/4.
8th Question
Question: The table summarizes the distribution of color and shape for 100 tiles of equal area.
| . | Red | Blue | Yellow | Total |
|---|---|---|---|---|
| Square | 10 | 20 | 25 | 55 |
| Pentagon | 20 | 10 | 15 | 45 |
| Total | 30 | 30 | 40 | 100 |
If one of these tiles is selected at random, what is the probability of selecting a red tile? (Express your answer as a decimal or fraction, not as a percent.)
A) 0.55
B) 0.3
C) 0.7
D) 0.45
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 3/10. It’s given that there are a total of 100 tiles of equal area, which is the total number of possible outcomes. According to the table, there are a total of 30 red tiles. The probability of an event occurring is the ratio of the number of favorable outcomes to the total number of possible outcomes. By definition, the probability of selecting a red tile is given by 30/100, or 3/10. Note that 3/10 and 0.3 are examples of ways to enter a correct answer.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Understand Probability
The probability of an event is defined as:
Probability = Number of favorable outcomes/Total number of outcomes
Here:
~ Favorable outcomes are the red tiles.
~ Total outcomes are the total number of tiles (100).
Step 2: Identify the Relevant Data
From the table:
~ The total number of tiles is 100.
~ The total number of red tiles is:
~ ~ Red squares: 10
~ ~ Red pentagons: 20
The total number of red tiles is:
10 + 20 = 30
Step 3: Calculate the Probability
Using the probability formula:
Probability of selecting a red tile = Number of red tiles/Total number of tiles
~ Substitute the values:
Probability = 30/100
~ Simplify the fraction:
Probability = 3/10
~ Express as a decimal:
Probability = 0.3
Step 4: Verify the Answer
The total number of tiles is 100. The sum of red tiles (10 + 20 = 30) matches the total for red tiles in the table. Therefore, the calculations are correct.
Final Answer: The probability of selecting a red tile is: B) 0.3.
9th Question
f(x) = 2x + 3
Question: For the given function f, the graph of y = f(x) in the xy-plane is parallel to line j. What is the slope of line j?
A) 6
B) 5
C) 3
D) 2
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 2. It’s given that function f is defined by f(x) = 2x + 3. Therefore, the equation representing the graph of y = f(x) in the xy-plane is y = 2x + 3, and the graph is a line. For a linear equation in the form y = mx + b, m represents the slope of the line. Since the value of m in the equation y = 2x + 3 is 2, the slope of the line defined by function f is 2. It’s given that line j is parallel to the line defined by function f. The slopes of parallel lines are equal. Therefore, the slope of line j is also 2.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Question Explanation:
We are given the linear function f(x) = 2x + 3, and the graph of y = f(x) is parallel to another line j. The task is to find the slope of line j.
In mathematics, two lines are parallel if and only if they have the same slope. This means that the slope of line j will be equal to the slope of y = f(x).
Step-by-Step Solution:
Step 1: Understand the function f(x) = 2x + 3
The general form of a linear equation is:
y = mx + b
where:
~ m is the slope of the line.
~ b is the y-intercept (the value of y when x = 0).
For the given function f(x) = 2x + 3:
~ The slope (m) is 2.
~ The y-intercept (b) is 3.
Step 2: Parallel lines and slopes
~ Two lines are parallel if and only if their slopes are equal.
~ Since the slope of y = f(x) = 2x + 3 is 2, the slope of line j must also be 2 for it to be parallel.
Step 3: Verify the Answer
~ The slope of y = f(x) is given by the coefficient of x, which is 2.
~ The problem specifies that the two lines are parallel, so the slope of line j must also be 2.
Final Answer: The slope of line j is: D) 2.
10th Question
Question: A proposal for a new library was included on an election ballot. A radio show stated that 3 times as many people voted in favor of the proposal as people who voted against it. A social media post reported that 15,000 more people voted in favor of the proposal than voted against it. Based on these data, how many people voted against the proposal?
A) 7,500
B) 15,000
C) 22,500
D) 45,000
Choice A is correct. It’s given that a radio show stated that 3 times as many people voted in favor of the proposal as people who voted against it. Let x represent the number of people who voted against the proposal. It follows that 3x is the number of people who voted in favor of the proposal and 3x – x, or 2x, is how many more people voted in favor of the proposal than voted against it. It’s also given that a social media post reported that 15,000 more people voted in favor of the proposal than voted against it. Thus, 2x = 15,000. Since 2x = 15,000, the value of x must be half of 15,000, or 7,500. Therefore, 7,500 people voted against the proposal.
Choice B is incorrect. This is how many more people voted in favor of the proposal than voted against it, not the number of people who voted against the proposal.
Choice C is incorrect. This is the number of people who voted in favor of the proposal, not the number of people who voted against the proposal.
Choice D is incorrect and may result from conceptual or calculation errors.
Question Explanation:
We are tasked with finding how many people voted against the proposal for a new library. Two key pieces of information are provided:
1) The number of people who voted in favor of the proposal is 3 times the number of people who voted against it.
2) 15,000 more people voted in favor than voted against it.
This can be solved using algebra.
Step-by-Step Solution:
Step 1: Define the variables
Let:
~ x = the number of people who voted against the proposal.
~ 3x = the number of people who voted in favor of the proposal (based on the given ratio of 3 : 1).
Step 2: Set up the equation
We know from the problem that the number of people who voted in favor was 15,000 more than the number of people who voted against. Using this information, we write:
3x = x + 15,000
Step 3: Solve the equation
1) Subtract x from both sides to isolate x on one side:
3x − x = 15,000
2) Simplify: 2x = 15,000
3) Divide both sides by 2 to solve for x:
x = 15,000/2
x = 7,500
Step 4: Verify the solution
If x = 7,500, this means:
~ The number of people who voted against is 7,500.
~ The number of people who voted in favor is:
3x = 3(7,500) = 22,500
Check if the difference between the votes in favor and against is 15,000:
22,500 − 7,500 = 15,000
This matches the information given in the problem. Thus, the solution is correct.
Final Answer: The number of people who voted against the proposal is: A) 7,500.
11th Question
Question: A right circular cylinder has a volume of 432 cubic centimeters. The area of the base of the cylinder is 24 square centimeters. What is the height, in centimeters, of the cylinder?
A) 18
B) 24
C) 216
D) 10,368
Choice A is correct. The volume, V, of a right circular cylinder is given by the formula V = πr2h, where πr2 is the area of the base of the cylinder and h is the height. It’s given that a right circular cylinder has a volume of 432 cubic centimeters and the area of the base is 24 square centimeters. Substituting 432 for V and 24 for πr2 in the formula V = πr2h yields 432 = 24h. Dividing both sides of this equation by 24 yields 18 = h. Therefore, the height of the cylinder, in centimeters, is 18.
Choice B is incorrect. This is the area of the base, in square centimeters, not the height, in centimeters, of the cylinder.
Choice C is incorrect. This is the height, in centimeters, of a cylinder if its volume is 432 cubic centimeters and the area of its base is 2, not 24, cubic centimeters.
Choice D is incorrect. This is the height, in centimeters, of a cylinder if its volume is 432 cubic centimeters and the area of its base is 1/24, not 24, cubic centimeters.
Let’s use the formula for the volume of a cylinder in terms of its radius (r) and height (h), which is:
V = πr2h
This formula is derived from the fact that the area of the base of a cylinder is the area of a circle (πr2) and the volume is the product of the base area and the height.
Step-by-Step Solution
Step 1: Write down the formula
V = πr2h
Step 2: Substitute the known values
From the problem:
~ The volume V = 432 cm3,
~ The base area Abase = πr2 = 24 cm2.
Since πr2 = 24, the formula becomes:
432 = 24 ⋅ h
Step 3: Solve for h
To isolate h, divide both sides by 24:
h = 432/24
Perform the division: h = 18
Why This Formula?
The formula V = πr2h directly calculates the volume of a cylinder. Here’s why:
1) The base of a cylinder is a circle, so the area of the base is given by πr2.
2) The height (h) tells us how far this circular base is “stretched” into the third dimension to form the cylinder.
3) Multiplying the base area by the height gives the total volume.
In this specific problem, the area of the base (πr2) was already provided as 24 cm2, so we didn’t need to calculate r separately. This simplified the solution.
Verification
Substitute h = 18 back into the volume formula:
V = πr2h
V = 24 ⋅ 18
V = 432 cm3
The calculation is correct, confirming h = 18 cm.
Final Answer: A) 18 cm.
Volume is in cubic centimeters (cm3):
The volume of a cylinder represents the space it occupies in three dimensions. Since the cylinder extends in three dimensions (length, width, and height), the unit of measurement for its volume is cubic centimeters (cm3).
~ The formula for the volume of a cylinder is V = πr2h.
~ Here, πr2 gives the area of the base (in cm2), and when we multiply the base area by the height (h, in cm), we get a measurement in cm3.
~ Think of it as stacking h layers of the circular base (πr2) on top of each other to fill up the cylinder.
Why the Units are Different:
1) Square units (cm2) are used for the area because the area is a two-dimensional measurement.
2) Cubic units (cm3) are used for volume because volume is a three-dimensional measurement.
12th Question
x2 = -841
Question: How many distinct real solutions does the given equation have?
A) Exactly one
B) Exactly two
C) Infinitely many
D) Zero
Choice D is correct. Since the square of a real number is never negative, the given equation isn’t true for any real value of x. Therefore, the given equation has zero distinct real solutions.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Question Analysis
The given equation is:
x2 = −841
We need to determine how many distinct real solutions this equation has. Let’s solve it step-by-step.
Step 1: What does x2 = −841 mean?
The equation states that x, when squared, equals −841. However, no real number, when squared, results in a negative value because:
~ The square of any real number (positive or negative) is always non-negative. For example:
(+29)2 = 841 and (−29)2 = 841
Thus, x2 = −841 has no real solutions because the left-hand side (x2) is always non-negative, while the right-hand side (−841) is negative.
Step 2: Determine the number of solutions
Since x2 = −841 is impossible for any real number x, there are:
Zero real solutions.
Why the Other Choices Are Incorrect
Choice A (Exactly one): Incorrect because there are no real solutions.
Choice B (Exactly two): Incorrect because ±29i are imaginary, not real, solutions.
Choice C (Infinitely many): Incorrect because no real solutions exist for this equation.
Final Answer: D) Zero.
But if it was x2 = 841 then there are two solutions.
Step 1: What does x2 = 841 mean?
This equation states that x, when squared, equals 841. To solve for x, we need to find all the real numbers whose squares equal 841.

Step 4: Number of distinct real solutions
Since there are two distinct values (+29 and −29) that satisfy the equation, the equation has exactly two distinct real solutions.
Step 5: Verify the solutions
Substitute each solution back into the original equation to verify:
1) For x = 29: (29)2 = 841(True!)
2) For x = −29: (−29)2 = 841(True!)
Both solutions are correct.
Answer
The equation has exactly two distinct real solutions.
The correct answer is: B) Exactly two.
13th Question
Question: Line k is defined by y = 7x + 1/8. Line j is perpendicular to line k in the xy-plane. What is the slope of line j?
A) −8
B) −1/7
C) 1/8
D) 7
Choice B is correct. It’s given that line k is defined by y = 7x + 1/8. For an equation in slope-intercept form y = mx + b, m represents the slope of the line defined by this equation in the xy-plane and b represents the y-coordinate of the y-intercept of this line. Therefore, the slope of line k is 7. It’s also given that line j is perpendicular to line k in the xy-plane. Therefore, the slope of line j is the opposite reciprocal of the slope of line k. The opposite reciprocal of 7 is -1/7. Therefore, the slope of line j is -1/7.
Choice A is incorrect. This is the opposite reciprocal of the y-coordinate of the y-intercept, not the slope, of line k.
Choice C is incorrect. This is the y-coordinate of the y-intercept of line k, not the slope of line j.
Choice D is incorrect. This is the slope of a line that is parallel, not perpendicular, to line k.
Question Analysis
We are tasked with finding the slope of line j, which is perpendicular to line k. The given equation for line k is:
y = 7x + 1/8
The slope of line k is the coefficient of x, which is 7.
We need to use the relationship between slopes of perpendicular lines to determine the slope of line j.
Key Steps to Identify Slope and Y-Intercept
1) Start with the equation in slope-intercept form:
y = mx + b
~ m: The coefficient of x, which represents the slope.
~ b: The constant term, representing the y-intercept.
2) For the given equation y = 7x + 1/8:
~ The slope m = 7.
~ The y-intercept b = 1/8.
3) When dealing with perpendicular lines:
~ Find the slope of the given line.
~ Take the opposite reciprocal of that slope to find the slope of the perpendicular line.
Step 1: Relationship Between Perpendicular Slopes
For two lines to be perpendicular, the product of their slopes must equal −1. If m1 is the slope of one line and m2 is the slope of the other line, then:
m1 ⋅ m2 = −1
Here, the slope of line k (m1) is 7. The slope of line j (m2) is unknown. Substituting m1 = 7 into the equation:
7 ⋅ m2 = −1
Step 2: Solve for m2
To find m2, divide both sides of the equation by 7:
m2 = −1/7
Thus, the slope of line j is: −1/7.
Step 3: Verify
To confirm, if m1 = 7 and m2 = −1/7, their product is:
m1 ⋅ m2 = 7 ⋅ (−1/7) = −1 = -1
This satisfies the condition for perpendicular lines, verifying that the slope of line j is indeed −1/7.
Final Answer: The slope of line j is: B) −1/7.
Why Other Aspects of the Equation Are Irrelevant
1) The y-intercept (1/8) of line k does not affect the slope or perpendicularity — only the slope matters for this calculation.
2) The perpendicular relationship is purely based on the negative reciprocal rule.
Understanding “Coefficient of x” in Slope-Intercept Form
The coefficient of x, m, tells us the steepness of the line and whether it is increasing or decreasing:
y = mx + b
y = 3x + 1 (m = 3, b = 1)
~ m: The slope m describes the steepness or inclination of a line in the xy-plane. It tells you how much y changes for a unit change in x.
~ b = Unit change in x.
1) Positive Coefficient (m > 0):
~ The line slopes upward as x increases (moving left to right).
~ Example: If y = 3x + 1, the coefficient of x is 3, meaning the line rises by 3 units for every 1 unit increase in x. (If m = 3, this means that for every 1 unit increase in x, y increases by 3 units.)
2) Negative Coefficient (m < 0):
~ The line slopes downward as x increases.
~ Example: If y = −2x + 5, the coefficient of x is -2, meaning the line falls by 2 units for every 1 unit increase in x.
3) Zero Coefficient (m = 0):
~ The line is horizontal (flat) because y does not change as x changes.
~ Example: y = 5 is a horizontal line.
14th Question
Question:
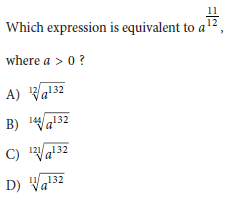
Choice B

Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Question Explanation:
The goal is to simplify and find an equivalent expression for a11/12. Let’s break this problem into detailed steps and solve it.
Step-by-Step Explanation:

Let’s try to solve all options to find the best one.

Learn to use the Desmos calculator for quick solutions.
15th Question
Question: An event planner is planning a party. It costs the event planner a one-time fee of $35 to rent the venue and $10.25 per attendee. The event planner has a budget of $200. What is the greatest number of attendees possible without exceeding the budget?
A) 16
B) 17
C) 32
D) 33
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 16. The total cost of the party is found by adding the one-time fee of the venue to the cost per attendee times the number of attendees. Let x be the number of attendees. The expression 35 + 10.25x thus represents the total cost of the party. It’s given that the budget is $200, so this situation can be represented by the inequality 35 + 10.25x < 200. The greatest number of attendees can be found by solving this inequality for x. Subtracting 35 from both sides of this inequality gives 10.25x < 165. Dividing both sides of this inequality by 10.25 results in approximately x < 16.098. Since the question is stated in terms of attendees, rounding x down to the nearest whole number, 16, gives the greatest number of attendees possible.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect and may result from conceptual errors.
Choice D is incorrect and may result from conceptual errors.
Step-by-Step Solution
Step 1: Define the Variables
Let x represent the number of attendees. The total cost for the event includes:
1) A fixed cost of $35 for renting the venue.
2) A variable cost of $10.25 per attendee.
The total cost, therefore, can be modeled as:
Total Cost = 35 + 10.25x
Step 2: Write an Inequality
The planner’s budget is $200, so the total cost must not exceed this budget:
35 + 10.25x ≤ 200
Step 3: Solve the Inequality
To solve for x, follow these steps:
1) Subtract the fixed cost of $35 from both sides:
10.25x ≤ 200 − 35
10.25x ≤ 165
2) Divide both sides by the cost per attendee ($10.25) to isolate x:
x ≤ 165/10.25
x ≤ 16.0976
Step 4: Interpret the Result
Since x represents the number of attendees, it must be an integer. The greatest whole number less than or equal to 16.0976 is 16.
Thus, the maximum number of attendees is:
x = 16
Step 5: Verify the Answer
To ensure that x = 16 fits within the budget, calculate the total cost:
Total Cost = 35 + 10.25(16)
Total Cost = 35 + 164 = 199
Since $199 is less than $200, the answer is valid. If we increase x to 17:
Total Cost = 35 + 10.25(17)
Total Cost = 35 + 174.25 = 209.25
This exceeds the budget. Therefore, x = 16 is indeed the greatest possible number of attendees.
Final Answer: The greatest number of attendees possible without exceeding the budget is: A) 16.
16th Question
y = 4x + 1
4y = 15x – 8
Question: The solution to the given system of equations is (x, y). What is the value of x − y?
A) 25
B) 35
C) 45
D) 55
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 35. The first equation in the given system of equations defines y as 4x + 1. Substituting 4x + 1 for y in the second equation in the given system of equations yields 4(4x + 1) = 15x – 8. Applying the distributive property on the left-hand side of this equation yields 16x + 4 = 15x – 8. Subtracting 15x from each side of this equation yields x + 4 = -8. Subtracting 4 from each side of this equation yields x = -12. Substituting -12 for x in the first equation of the given system of equations yields y = 4(-12) + 1, or y = -47. Substituting -12 for x and -47 for y into the expression x – y yields -12 – (-47), or 35.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
We are solving a system of two linear equations:
y = 4x + 1
4y = 15x − 8
The goal is to find the solution for x and y, and then calculate x − y.
Step-by-Step Solution
Step 1: Substitute y = 4x + 1 into the second equation
We are given y = 4x + 1. Substituting this expression for y in the second equation:
4(4x + 1) = 15x − 8
Step 2: Simplify the equation
Expand 4(4x + 1):
16x + 4 = 15x − 8
Move all terms involving x to one side and constants to the other:
16x − 15x = −8
x = −12
Step 3: Solve for y
Now substitute x = −12 into the first equation y = 4x + 1:
y = 4(−12) + 1
y = −48 + 1
y = −47
Step 4: Calculate x − y
The problem asks for x − y:
x − y = −12 − (−47)
x − y = −12 + 47
x – y = 35
Verification
1) Substitute x = −12 and y = −47 into both equations to ensure they are satisfied:
~ First equation: y = 4x + 1:
−47 = 4(−12) + 1
−47 = −48 + 1 (Correct.)
~ Second equation: 4y = 15x − 8:
4(−47) = 15(−12) −8
−188 = −180 − 8 (Correct.)
2) Both equations are satisfied, confirming the solution is correct.
Final Answer: The value of x − y is: B) 35.
17th Question
5x2 + 10x + 16 = 0
Question: How many distinct real solutions does the given equation have?
A) Exactly one
B) Exactly two
C) Infinitely many
D) Zero
Choice D is correct. The number of solutions of a quadratic equation of the form ax2 + bx + c = 0, where a, b, and c are constants, can be determined by the value of the discriminant, b2 – 4ac. If the value of the discriminant is positive, then the quadratic equation has exactly two distinct real solutions. If the value of the discriminant is equal to zero, then the quadratic equation has exactly one real solution. If the value of the discriminant is negative, then the quadratic equation has zero real solutions. In the given equation, 5x2 + 10x + 16 = 0, a = 5, b = 10, and c = 16. Substituting these values for a, b, and c in b2 – 4ac yields (10)2 – 4(5 )(16), or -220. Since the value of its discriminant is negative, the given equation has zero real solutions. Therefore, the number of distinct real solutions the given equation has is zero.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation
To determine how many distinct real solutions the given quadratic equation 5x2 + 10x + 16 = 0 has, we need to calculate its discriminant using the formula:
Δ = b2 − 4ac
where a, b, and c are the coefficients of the quadratic equation ax2 + bx + c = 0.
Step 1: Identify coefficients
From the equation 5x2 + 10x + 16 = 0:
~ a = 5
~ b = 10
~ c = 16
Step 2: Substitute into the discriminant formula
Δ = b2 − 4ac
Substitute b = 10, a = 5, and c = 16:
Δ = 102 − 4(5)(16)
Δ = 100 − 320
Δ = −220
Step 3: Interpret the discriminant
The discriminant Δ = −220 is negative.
~ A negative discriminant means the quadratic equation has no real solutions. Instead, it has two complex solutions.
Step 4: Verify the answer
The discriminant confirms that the equation has no distinct real solutions, so the correct answer is: D) Zero.
Why does a negative discriminant indicate no real solutions?
The solutions of a quadratic equation are given by the quadratic formula:
~ If Δ > 0, the square root of the discriminant is a positive number, leading to two distinct real solutions.
~ If Δ = 0, the square root of the discriminant is zero, leading to exactly one real solution.
~ If Δ < 0, the square root of the discriminant is imaginary, resulting in no real solutions.
Final Answer: D) Zero.
18th Question
Question: A certain park has an area of 11,863,808 square yards. What is the area, in square miles, of this park? (1 mile = 1,760 yards)
A) 1.96
B) 3.83
C) 3,444.39
D) 6,740.8
Choice B is correct. Since 1 mile is equal to 1,760 yards, 1 square mile is equal to 1,7602, or 3,097,600, square yards. It’s given that the park has an area of 11,863,808 square yards. Therefore, the park has an area of (11,863,808 square yards)( 1 square mile/3,097,600 square yards), or 11,863,808/3,097,600 square miles. Thus, the area, in square miles, of the park is 3.83.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect. This is the square root of the area of the park in square yards, not the area of the park in square miles.
Choice D is incorrect and may result from converting 11,863,808 yards to miles, rather than converting 11,863,808 square yards to square miles.
Step-by-Step Explanation
We are tasked with converting the given area of the park from square yards to square miles. To solve this, we will follow these steps:
Step 1: Understand the relationship between yards and miles
~ 1 mile = 1,760 yards
~ Since area is measured in square units, we need to square both sides of this relationship:
~ 1 square mile = (1,760)2 square yards
~ 1 square mile = 3,097,600 square yards
Step 2: Divide the total square yards by the number of square yards in a square mile
The total area of the park is 11,863,808 square yards.
To convert this into square miles, divide by 3,097,600:
Area in square miles = 11,863,808/3,097,600
Step 3: Perform the division
Area in square miles = 3.83
Step 4: Verify the calculation
To ensure accuracy, perform the division again:
Area in square miles = 11,863,808/3,097,600 = 3.83
Final Answer: The area of the park is: B) 3.83 square miles.
19th Question
Question: Which of the following equations represents a circle in the xy-plane that intersects the y-axis at exactly one point?
A) (x − 8)2 + (y − 8)2 = 16
B) (x − 8)2 + (y − 4)2 = 16
C) (x − 4)2 + (y − 9)2 = 16
D) x2 + (y − 9)2 = 16
Choice C is correct. The graph of the equation (x – h)2 + (y – k)2 = r2 in the xy-plane is a circle with center (h, k) and a radius of length r. The radius of a circle is the distance from the center of the circle to any point on the circle. If a circle in the xy-plane intersects the y-axis at exactly one point, then the perpendicular distance from the center of the circle to this point on the y-axis must be equal to the length of the circle’s radius. It follows that the x-coordinate of the circle’s center must be equivalent to the length of the circle’s radius. In other words, if the graph of (x – h)2 + (y – k)2 = r2 is a circle that intersects the y-axis at exactly one point, then r = h must be true. The equation in choice C is (x – 4)2 + (y – 9)2 = 16, or (x – 4)2 + (y – 9)2 = 42. This equation is in the form (x – h)2 + (y – k)2 = r2, where h = 4, k = 9, and r = 4, and represents a circle in the xy-plane with center (4, 9) and radius of length 4. Substituting 4 for r and 4 for h in the equation r = |h| yields 4 = |4|, or 4 = 4, which is true. Therefore, the equation in choice C represents a circle in the xy-plane that intersects the y-axis at exactly one point.
Choice A is incorrect. This is the equation of a circle that does not intersect the y-axis at any point.
Choice B is incorrect. This is an equation of a circle that intersects the x-axis, not the y-axis, at exactly one point.
Choice D is incorrect. This is the equation of a circle with the center located on the y-axis and thus intersects the y-axis at exactly two points, not exactly one point.
Step 1: Understand the equation of a circle
The equation of a circle is given by:
(x − h)2 + (y − k)2 = r2
~ (h, k) is the center of the circle.
~ r is the radius of the circle.
If a circle intersects the y-axis at exactly one point, the perpendicular distance from the center of the circle to the y-axis must be equal to the radius of the circle. This means:
r = ∣h∣
Here, h is the x-coordinate of the center of the circle, and r is the radius.
Step 2: Analyze each choice
We will test each equation to determine if it meets the condition r = ∣h∣, which ensures that the circle intersects the y-axis at exactly one point.
Option A: (x − 8)2 + (y − 8)2 = 16
1) This equation is in the form: (x − h)2 + (y − k)2 = r2 where h = 8, k = 8, and r2 = 16.
~ Solving for r:
r = square root of 16
r = 4
2) Check the condition r = ∣h∣:
r = 4
∣h∣ = ∣8∣ = 8
Since r ≠ ∣h∣, the circle does not intersect the y-axis at exactly one point.
Option A is incorrect.
Option B: (x − 8)2 + (y − 4)2 = 16
1) This equation is in the form:
(x − h)2 + (y − k)2 = r2
where h = 8, k = 4, and r2 = 16.
Solving for r:
r = square root of 16
r = 4
2) Check the condition r = ∣h∣:
r = 4
∣h∣ = ∣8∣ = 8
Since r ≠ ∣h∣, the circle does not intersect the y-axis at exactly one point.
Option B is incorrect.
Option C: (x − 4)2 + (y − 9)2 = 16
1) This equation is in the form:
(x − h)2 + (y − k)2 = r2
where h = 4, k = 9, and r2 = 16.
Solving for r:
r = 16
r = 4
2) Check the condition r = ∣h∣:
r = 4
∣h∣ = ∣4∣ = 4
Since r = ∣h∣, the circle intersects the y-axis at exactly one point.
Option C is correct.
Option D: x2 + (y − 9)2 = 16
1) This equation is in the form:
(x − h)2 + (y − k)2 = r2
here h = 0, k = 9, and r2 = 16.
Solving for r:
r = 16
r = 4
2) Check the condition r = ∣h∣:
r = 4
∣h∣ = ∣0∣ = 0
Since r ≠ ∣h∣, the circle does not intersect the y-axis at exactly one point.
Option D is incorrect.
Step 3: Final Answer: C) (x − 4)2 + (y − 9)2 = 16.
Why r = ∣h∣?
The equation of a circle in the xy-plane is:
(x − h)2 + (y − k)2 = r2
Where:
~ (h, k) is the center of the circle.
~ r is the radius of the circle.
A circle intersects the y-axis where x = 0. To check where the circle intersects the y-axis, we substitute x = 0 into the equation:
(0 − h)2 + (y − k)2 = r2
Simplifying:
h2 + (y − k)2 = r2
For the circle to intersect the y-axis at exactly one point, the distance from the center of the circle to the y-axis (which is ∣h∣) must equal the radius of the circle. This ensures that the radius only reaches the y-axis at a single point.
Geometric Explanation of r = ∣h∣
~ ∣h∣ represents the horizontal distance from the center of the circle to the y-axis.
~ r represents the radius of the circle, which is the distance from the center to any point on the circle.
~ If ∣h∣ > r, the circle will not touch the y-axis.
~ If ∣h∣ < r, the circle will intersect the y-axis at two points.
~ If ∣h∣ = r, the circle will “just touch” the y-axis at exactly one point.
This is why the condition r = ∣h∣ is used to determine whether a circle intersects the y-axis at exactly one point.
What does ∣h∣ mean?
The notation ∣h∣ represents the absolute value of h. The absolute value of a number is its distance from 0 on the number line, regardless of direction. For example:
~ ∣4∣ = 4
~ ∣−4∣ = 4
In this context, ∣h∣ gives the distance between the center of the circle and the y-axis, which is always positive (Because it expands, not contract).
Why not k = r?
~ (h, k) is the center of the circle.
~ ~ h = horizontal line from center
~ ~ k = vertical line from center
~ r is the radius.
~ The variable k represents the y-coordinate of the center of the circle. This determines the circle’s vertical position but does not relate to how the circle interacts with the y-axis.
~ The key condition for the circle to touch the y-axis is based on the horizontal distance from the center to the y-axis, which depends on h, not k.
20th Question
Question: In triangles ABC and DEF, angles B and E each have measure 27° and angles C and F each have measure 41°. Which additional piece of information is sufficient to determine whether triangle ABC is congruent to triangle DEF?
A) The measure of angle A
B) The length of side AB
C) The lengths of sides BC and EF
D) No additional information is necessary.
Choice C is correct. Since angles B and E each have the same measure and angles C and F each have the same measure, triangles ABC and DEF are similar, where side BC corresponds to side EF. To determine whether two similar triangles are congruent, it is sufficient to determine whether one pair of corresponding sides is congruent. Therefore, to determine whether triangles ABC and DEF are congruent, it is sufficient to determine whether sides BC and EF have equal lengths. Thus, knowing the lengths of BC and EF is sufficient to determine whether triangle ABC is congruent to triangle DEF.
Choice A is incorrect and may result from conceptual errors.
Choice B is incorrect and may result from conceptual errors.
Choice D is incorrect. The given information is sufficient to determine that triangles ABC and DEF are similar, but not whether they are congruent.
Step-by-Step Solution:
Step 1: Analyze the given information
We are given:
~ In triangle ABC:
∠B = 27°
∠C = 41°
~ In triangle DEF:
∠E = 27°
∠F = 41°
From the Triangle Sum Theorem, which states that the sum of the interior angles of a triangle is always 180°:
∠A = 180° − ∠B − ∠C
∠A = 180° − 27° − 41°
∠A = 112°
Similarly, in triangle DEF:
∠D = 180° − ∠E − ∠F
∠D = 180° − 27° − 41°
∠D = 112°
Thus, all three angles of triangle ABC are equal to the corresponding angles of triangle DEF:
~ ∠A = ∠D = 112°
~ ∠B = ∠E = 27°
~ ∠C = ∠F = 41°
This tells us that triangles ABC and DEF are similar by the AA (Angle-Angle) Similarity Postulate, but this does not guarantee congruence.
Step 2: Recall the conditions for congruence
Two triangles are congruent if they satisfy any of the following criteria:
1) SSS (Side-Side-Side): All three corresponding sides are equal.
2) SAS (Side-Angle-Side): Two corresponding sides and the included angle are equal.
3) ASA (Angle-Side-Angle): Two corresponding angles and the included side are equal.
4) AAS (Angle-Angle-Side): Two corresponding angles and a non-included side are equal.
5) HL (Hypotenuse-Leg): Only for right triangles.
Step 3: Determine which additional information is sufficient
Since △ABC and △DEF are already similar, we need information about the corresponding sides to check for congruence.
Option A: The measure of angle A
This is unnecessary because we already know that all three angles of the two triangles are equal. Angle A does not help determine congruence.
Option B: The length of side AB
Knowing the length of only one side is not sufficient because it does not provide enough information about the size of the other triangle. The triangles could be similar but scaled differently.
Option C: The lengths of sides BC and EF
If we know the lengths of corresponding sides BC and EF, we can compare their ratio. If the ratio is 1 (i.e., the sides are equal), the triangles are congruent by the SAS Congruence Postulate because we already know the included angles (∠B = ∠E) are equal.
This option is sufficient.
Option D: No additional information is necessary
This is incorrect because similar triangles are not necessarily congruent unless we verify that their corresponding sides are equal.
Verification:
~ Given that ∠B = ∠E = 27° and ∠C = ∠F = 41°, we establish similarity between the two triangles.
~ To determine congruence, we need side length information.
~ Knowing two corresponding sides (like BC and EF) and verifying their equality ensures congruence through the SAS Congruence Postulate.
Final Answer: C) The lengths of sides BC and EF
21th Question
Question: A circle in the xy-plane has its center at (−1, 1). Line t is tangent to this circle at the point (5, −4). Which of the following points also lies on line t?
A) (0, 6/5)
B) (4, 7)
C) (10, 2)
D) (11, 1)
Choice C is correct. It’s given that the circle has its center at (-1, 1) and that line t is tangent to this circle at the point (5, -4). Therefore, the points (-1, 1) and (5, -4) are the endpoints of the radius of the circle at the point of tangency. The slope of a line or line segment that contains the points (a, b) and (c, d) can be calculated as d – b/c – a. Substituting (-1, 1) for (a, b) and (5, -4) for (c, d) in the expression d – b/c – a yields -4 – 1/5 – (-1), or -5/6. Thus, the slope of this radius is -5/6. A line that’s tangent to a circle is perpendicular to the radius of the circle at the point of tangency. It follows that line t is perpendicular to the radius at the point (5, -4), so the slope of line t is the negative reciprocal of the slope of this radius. The negative reciprocal of -5/6 is 6/5. Therefore, the slope of line t is 6/5. Since the slope of line t is the same between any two points on line t, a point lies on line t if the slope of the line segment connecting the point and (5, -4) is 6/5. Substituting choice C, (10, 2), for (a, b) and (5, -4) for (c, d) in the expression d – b/c – a yields -4 – 2/5 – 10, or 6/5. Therefore, the point (10, 2) lies on line t.
Choice A is incorrect. The slope of the line segment connecting (0, 6/5) and (5, -4) is -4 -6/5 divided by 5 – 0, or -26/25, not 6/5.
Choice B is incorrect. The slope of the line segment connecting (4, 7) and (5, -4) is -4 – 7/5 – 4, or -11, not 6/5.
Choice D is incorrect. The slope of the line segment connecting (11, 1) and (5, -4) is -4 – 1/5 – 11, or 5/6, not 6/5.
Step-by-Step Solution:
Step 1: Analyze the information provided
~ The circle is centered at (−1, 1) with an unspecified radius.
~ Line t is tangent to the circle at the point (5, −4).
~ We are tasked with determining which of the given points lies on line t.
Step 2: Properties of a tangent line

Step 3: Equation of the tangent line
The equation of a line can be written in point-slope form:
y − y1 = m(x − x1)
where:
~ m is the slope,
~ (x1, y1) is a point on the line.
Here:
m = 6/5 (the slope of the tangent line),
The tangent point is (x1, y1) = (5, −4).
Substitute these values:

Final Answer: B) (10, 2).
Why Use the Negative Reciprocal?
In the context of this problem, the negative reciprocal is used because the two lines (the radius and the tangent) are perpendicular to each other. This relationship between perpendicular lines dictates the need for the negative reciprocal. Let’s break it down step by step.
~ Perpendicular Lines:
~ ~ If two lines are perpendicular in the xy-plane, their slopes m1 and m2 satisfy the following relationship:
m1 ⋅ m2 = −1
~ ~ This means that one slope is the negative reciprocal of the other:
m2 = −1/m1
~ Reason for Negative Reciprocal:
~ Perpendicular lines meet at a right angle (90°).
~ The relationship m1 ⋅ m2 = −1 ensures that their slopes create this right angle geometrically.
22th Question
Question: For an electric field passing through a flat surface perpendicular to it, the electric flux of the electric field through the surface is the product of the electric field’s strength and the area of the surface. A certain flat surface consists of two adjacent squares, where the side length, in meters, of the larger square is 3 times the side length, in meters, of the smaller square. An electric field with a strength 29.00 volts per meter passes uniformly through this surface, which is perpendicular to the electric field. If the total electric flux of the electric field through this surface is ·4,640 volts ⋅ meters, what is the electric flux, in ·volts ⋅ meters, of the electric field through the larger square?
A) 5,129
B) 4,890
C) 4,640
D) 4,176
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 4,176. It’s given that the side length of the larger square is 3 times the side length of the smaller square. This means that the area of the larger square is 32, or 9, times the area of the smaller square. If the area of the smaller square is represented by x, then the area of the larger square can be represented by 9x. Therefore, the flat surface of the two adjacent squares has a total area of x + 9x, or 10x. It’s given that an electric field with strength 29.00 volts per meter passes uniformly through this surface and the total electric flux of the electric field through this surface is 4,640 volts . meters. Since it’s given that the electric flux is the product of the electric field’s strength and the area of the surface, the equation 29.00(10x) = 4,640, or 290x = 4,640, can be used to represent this situation. Dividing each side of this equation by 290 yields x = 16. Substituting 16 for x in the expression for the area of the larger square, 9x, yields 9(16), or 144, square meters. Since the area of the larger square is 144 square meters, the electric flux, in volts . meters, of the electric field through the larger square can be determined by multiplying the area of the larger square by the strength of the electric field. Thus, the electric flux is (144 square meters)(29.00 volts/meter), or 4,176 volts . meters.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Understanding the Question Word by Word:
1) “For an electric field passing through a flat surface perpendicular to it”:
~ This means an electric field moves straight (at a 90° angle) through a flat surface. The “perpendicular” nature ensures the electric field lines hit the surface directly, not at an angle.
2) “The electric flux of the electric field through the surface is the product of the electric field’s strength and the area of the surface”:
~ Electric flux measures how much of the electric field passes through a surface.
~ Formula for electric flux: Φ = E ⋅ A
Where:
Φ = Electric flux (volts ⋅ meters),
E = Electric field strength (volts/meter),
A = Area of the surface (meters2).
3) “A certain flat surface consists of two adjacent squares, where the side length, in meters, of the larger square is 3 times the side length, in meters, of the smaller square”:
~ There are two squares side by side: a smaller square and a larger square.
~ The side length of the larger square is 3 times the side length of the smaller square. If the smaller square’s side length is s, the larger square’s side length is 3s.
4) “An electric field with a strength 29.00 volts per meter passes uniformly through this surface, which is perpendicular to the electric field”:
~ The electric field strength (E) is given as 29.00 volts/meter, and it is uniform, meaning it has the same strength across both squares.
~ “Perpendicular” here means the entire area of both squares is effectively exposed to the electric field, so there is no need to adjust the flux formula. (Electric passes through both squares on the surface at a 90-degree angle.)
5) “If the total electric flux of the electric field through this surface is 4,640 volts · meters”:
~ The combined flux (Φtotal) through both squares is 4,640 volts · meters.
6) “What is the electric flux, in volts · meters, of the electric field through the larger square?”:
~ The question asks for the flux passing through the larger square, denoted as Φlarger.
Key Points and Common Misconceptions:
1) Why do we use 32, not 3x, for the larger square?
~ The side length of the larger square is 3s, but area is calculated as:
Area of a square = side length2
Therefore, the area of the larger square is:
Alarger = (3s)2 = 9s2
2) Why don’t we use the reciprocal of the slope (negative reciprocal)?
~ The “perpendicular” mentioned here does not refer to geometric lines but rather the orientation of the electric field relative to the surface. Since the electric field is perpendicular to the surface, the formula Φ = E ⋅ A applies directly without any angular adjustments.
Step-by-Step Solution:
1) Define Variables for the Squares:
~ Let the side length of the smaller square be s.
~ Area of the smaller square:
Asmaller = s2
~ Area of the larger square:
Alarger = (3s)2 = 9s2
2) Total Flux Through Both Squares:
~ The total flux is: Φtotal = Φsmaller + Φlarger
~ Using the formula Φ = E ⋅ Asmaller + Alarger
3) Substitute Areas and Total Flux:
~ Substituting Asmaller = s2 and Alarger = 9s2
Φtotal = E ⋅ s2 + E ⋅ 9s2
~ Combine terms:
Φtotal = E ⋅ (s2 + 9s2)
= E ⋅ 10s2
4) Solve for s2:
~ Substituting E = 29 volts/meter and Φtotal = 4,640 volts · meters:
4,640 = 29 ⋅ 10s2
~ Simplify: 4,640 = 290s2
~ Solve for s2:
s2 = 4,640/290 = 16 meters2
5) Calculate Flux Through the Larger Square:
~ Using Alarger = 9s2 and s2 = 16:
Alarger = 9 ⋅ 16 = 144 meters2
~ Flux through the larger square:
Φlarger = E ⋅ Alarger =
Φlarger = 29 ⋅ 144 = 4,176 volts · meters.
Final Answer: D) 4,176.
Did you try all the features and get comfortable using them? You should work on using the Desmos calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must attempt as many questions as you can before the final test. This is the 8th Practice Test of SAT Math Module 2nd.
Either you can take the 1st Practice Test of SAT Math or the 1st Practice Test of SAT Reading and Writing Module 2nd.
- SAT Test 1st (Math Module 2nd)
- SAT Test 8th (Math Module 1st)
- SAT Test 8th (Reading and Writing Module 2nd)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


