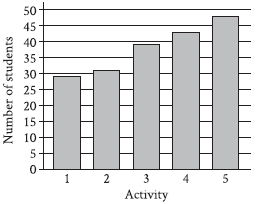
Question: A group of students voted on five after-school activities. The bar graph shows the number of students who voted for each of the five activities. How many students chose activity 3?
A) 25
B) 39
C) 48
D) 50

Choice B is correct. The height of each bar in the bar graph given represents the number of students who voted for the activity specified at the bottom of the bar. The bar for activity 3 has a height that is between 35 and 40. In other words, the number of students who chose activity 3 is between 35 students and 40 students. Of the given choices, 39 is the only value between 35 and 40. Therefore, 39 students chose activity 3.

Choice A is incorrect and may result from conceptual errors.

Choice C is incorrect. This is the number of students who chose Activity 5, not Activity 3.

Choice D is incorrect and may result from conceptual errors.

It is an easy one, because of the simple options. Wherever you see the text, that is its actual details.

Question: What percentage of 300 is 75?
A) 25%
B) 50%
C) 75%
D) 225%

Choice A:

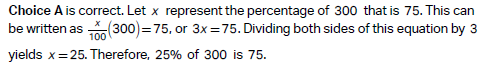
Choice B is incorrect. 50% of 300 is 150, not 75.

Choice C is incorrect. 75% of 300 is 225, not 75.

Choice D is incorrect. 225% of 300 is 675, not 75.

Another super easy way is to take numbers like 5, 10, or 100. In this case, Let’s take 5% and 10%, so 10% of 300 (just cross one 0 from each) is 30 and half of 30 is 15, that is 5% of 300. Now, we just break it down to get 75 (30 + 30 + 15 = 10% + 10% + 5%). If you want to use the calculator, you can use it from below.

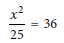
Question: What is a solution to the given equation?
A) 6
B) 30
C) 450
D) 900

Choice B is correct. Multiplying the left- and right-hand sides of the given equation by 25 yields x² = 900. Taking the square root of the left- and right-hand sides of this equation yields x = 30 or x = -30. Of these two solutions, only 30 is given as a choice.

Choice A is incorrect. This is a solution to the equation x² =36.

Choice C is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

When one side is on the divide and moves to the other side, it goes up. For example, 25 goes up to the other side and it will be 36 x 25 = 900. Either, you can learn the square root or do it using the Desmos calculator.

Step 1: Isolate x²
Since the equation has x² divided by 25, we can start by eliminating the fraction. To do this, multiply both sides of the equation by 25: x² = 36 × 25

Step 2: Multiply 36 by 25
Calculate the product: x² = 900

Step 3: Solve for x by Taking the Square Root

x = 30 Answer.

Question: 3 more than 8 times a number x is equal to 83. Which equation represents this situation?
A) (3)(8)x = 83
B) 8x = 83 + 3
C) 3x + 8 = 83
D) 8x + 3 = 83

Choice D is correct. The given phrase “8 times a number x ” can be represented by the expression 8x. The given phrase “3 more than” indicates an increase of 3 to a quantity. Therefore “3 more than 8 times a number x ” can be represented by the expression 8x + 3. Since it’s given that 3 more than 8 times a number x is equal to 83, it follows that 8x + 3 is equal to 83, or 8x + 3 = 83. Therefore, the
equation representing this situation is 8x + 3 = 83.

Choice A is incorrect. This equation represents 3 times the quantity 8 times a number x is equal to 83.

Choice B is incorrect. This equation represents 8 times a number x is equal to 3 more than 83.

Choice C is incorrect. This equation represents 8 more than 3 times a number x equals 83.

A few key words to learn to focus and find solutions quickly.
More than = Addition (+)
times = multiples [For example 8 times 10 is 10 x 8]
Equal to = As it sounds ‘similar to’ (=)

Step 1: Translate the Problem into Mathematical Terms
1. “8 times a number x”:
“8 times a number x” means multiplying x by 8, which we write as 8x.
2. “3 more than 8 times a number x”:
Adding 3 to 8x gives 8x + 3.
3. “is equal to 83”:
The phrase “is equal to” translates to an equals sign ‘=’
So, 8x + 3 = 83.

Step 2: Form the Equation
From these translations, we can write the equation as 8x + 3 = 83

Step 3: Check the Answer Choices
Let’s look at each answer choice to see if it matches our equation.
A) 3(8x) = 83
This option implies multiplying 3 by 8x, which does not match our equation.
B) 8x = 83 + 3
This option suggests that 8x is equal to 83 + 3, which is not correct because the addition of 3 is supposed to be on the left side, not the right side.
C) 8x = 3+83
This option also incorrectly places the addition on the right side rather than on the left with 8x.
D) 8x + 3 = 83
This option is correct because it matches the structure of the equation we derived.
So, the correct answer is: D) 8x + 3 = 83

Question: Hana deposited a fixed amount into her bank account each month. The function f(t) = 100 + 25t gives the amount, in dollars, in Hana’s bank account after t monthly deposits. What is the best interpretation of 25 in this context?
A) With each monthly deposit, the amount in Hana’s bank account increased by $25.
B) Before Hana made any monthly deposits, the amount in her bank account was $25.
C) After 1 monthly deposit, the amount in Hana’s bank account was $25.
D) Hana made a total of 25 monthly deposits.

Choice A is correct. It’s given that t represents the number of monthly deposits. In the given function f(t) = 100 + 25t, the coefficient of t is 25. This means that for every increase in the value of t by 1, the value of f(t) increases by 25. It follows that with each monthly deposit, the amount in Hana’s bank account increased by $25.

Choice B is incorrect. Before Hana made any monthly deposits, the amount in her bank account was $100.

Choice C is incorrect. After 1 monthly deposit, the amount in Hana’s bank account was $125.

Choice D is incorrect and may result from conceptual errors.

In math, you should consider options as well, to save some time, here they are you about the meaning of 25. If t represents monthly deposits then 25t means 25 x t. The equation is 100 + 25t, which means 100 is a stagnant amount but we add 25 x t every month. Add = increase.

The function given is: f(t) = 100 + 25t
where:
~ f(t) represents the total amount of money in Hana’s bank account after t monthly deposits.
~ t is the number of monthly deposits made.
~ The function can be interpreted as the starting amount in Hana’s account plus the amount she adds each month.

Step-by-Step Interpretation of Each Part of the Function
1. The Constant Term (100):
The 100 in the function represents the amount Hana initially had in her bank account before making any deposits. So, 100 is her starting balance.
2. The Coefficient of t (25):
The 25 is the coefficient of t, which represents how much Hana’s account balance increases each time she makes a deposit. Since this term is added every time t increases by 1 (i.e., every month), we can interpret 25 as the amount Hana deposits each month.

Answer Choices Analysis
Now let’s examine each answer choice based on our interpretation:
Option A: “With each monthly deposit, the amount in Hana’s bank account increased by $25.”
This option is correct. It accurately reflects that each month, Hana deposits $25 into her account, increasing her total balance by this amount.

Option B: “Before Hana made any monthly deposits, the amount in her bank account was $25.”
This option is incorrect. The initial amount in Hana’s account, before any deposits, is actually $100, not $25.

Option C: “After 1 monthly deposit, the amount in Hana’s bank account was $25.”
This option is incorrect because, after 1 month, the total amount would be 100 + 25 × 1 = 125.

Option D: “Hana made a total of 25 monthly deposits.”
This option is incorrect. The number 25 does not represent the total number of deposits. Instead, it represents the amount deposited each month.

Question: How many yards are equivalent to 1,116 inches? (1 yard = 36 inches)
A) 38
B) 31
C) 34
D) 36
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

Choice B:

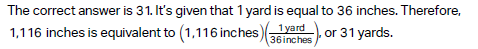
Choice A is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

Detailed Explanation of the Process
Understanding the relationship: Since 1 yard = 36 inches, we know that inches are smaller units than yards. Therefore, we need to divide the larger value (in inches) by the number of inches in a yard to convert to the larger unit (yards).
Setting up the equation: We use a straightforward proportional conversion formula to divide the total inches by 36.
Performing the calculation: Dividing 1,116 by 36 gives 31 exactly, with no remainder. This means the conversion is exact.

It would be best to use the Desmos calculator, so I suggest understanding its user interface properly before the final test.

Question: f(x) = 14 + 4x
The function f represents the total cost, in dollars, of attending an arcade when x games are played. How many games can be played for a total cost of $58?
A) 14
B) 13
C) 12
D) 11
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

Choice D: The correct answer is 11. It’s given that the function f(x) = 14 + 4x represents the
total cost, in dollars, of attending an arcade when x games are played. Substituting 58 for f(x) in the given equation yields 58 = 14 + 4x. Subtracting 14 from each side of this equation yields 44 = 4x. Dividing each side of this equation by 4 yields 11 = x. Therefore, 11 games can be played for a total cost of $58.

Choice A is incorrect and may result from conceptual or calculation errors.

Choice B is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

We know ‘the function f’ represents the total cost which is $58. The function f means f(x). If it is only written ‘f’ then it might complicate things.

Detailed Explanation of the Process
1. Understanding the equation: The given function f(x) = 14 + 4x is a linear function where the total cost is determined by adding a fixed cost (entry fee) to a variable cost (cost per game multiplied by the number of games).
2. Setting up the equation: Since we know the total cost is $58, we substitute f(x) = 58 into the function and solve for x.
3. Solving step-by-step: Subtracting the fixed cost of $14 from the total cost leaves us with $44, which represents the total cost of playing games. Dividing this by $4 (cost per game) gives the number of games.
4. Interpreting the result: The result x = 11 means that 11 games can be played while keeping the total cost exactly $58.

Question: f(x) = x + b
For the linear function f, b is a constant. When x = 0, f(x) = 30. What is the value of b?
A) −30
B) ⁻¹/₃₀
C) ¹/₃₀
D) 30

Choice D is correct. It’s given that when x = 0, f(x) = 30. Substituting 0 for x and 30 for f(x) in the given function yields 30 = 0 + b, or 30 = b. Therefore, the value of b is 30.

Choice B is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

We have values for everything, so we do not need to calculate. If x is 0 and x + b is 30, then we already know ‘b’ is also 30.

Explanation of the Process
1. Understanding the role of b: In the equation f(x) = x + b, b represents the y-intercept of the linear function. The y-intercept is the value of the function when x = 0.
2. Substituting the given values: Since x = 0 and f(x) = 30, we substitute these into the equation to directly solve for b.
3. Interpreting the result: The result b = 30 means that the value of the function when x = 0 is 30, which aligns with the given condition.

Step-by-Step Solution
Step 1: Understand the function
The function f(x) = x + b represents a linear function. In this equation:
~ x is the independent variable.
~ b is the y-intercept or the constant term.
~ f(x) represents the value of the function for a given x.
Step 2: Use the given information
We are told that when x = 0, f(x) = 30. Substitute x = 0 and f(x) = 30 into the equation f(x) = x + b:
f(x) = x + b
30 = 0 + b
Step 3: Solve for b
Simplify the equation:
b = 30 Answer.

Question: P(t) = 1,800(1.02)^t
The function P gives the estimated number of marine mammals in a certain area, where t is the number of years since a study began. What is the best interpretation of P(0) = 1,800 in this context?
A) The estimated number of marine mammals in the area was 102 when the study began.
B) The estimated number of marine mammals in the area was 1,800 when the study began.
C) The estimated number of marine mammals in the area increased by 102 each year during the study.
D) The estimated number of marine mammals in the area increased by 1,800 each year during the study.

Choice B is correct. The function P gives the estimated number of marine mammals in a certain area, where t is the number of years since a study began. Since the value of P(0) is the value of P(t) when t = 0, it follows that P(0) = 1,800 means that the value of P(t) is 1,800 when t = 0. Since t is the number of years since the study began, it follows that t = 0 is 0 years since the study began, or when the study began. Therefore, the best interpretation of P(0) = 1,800 in this context is the estimated number of marine mammals in the area was 1,800 when the study began.

Choice A is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

An option focus-based question, so don’t waste much time solving the question. Remember the most important tip, “The less the question rank, the less difficulty it contains.” So, this is a 9th question, nobody will ask you something complex. Now, based on the question, were asked about 1800, so Option A and Option C are out of reach.

Explanation of the Process
1. The meaning of t = 0: In the function P(t), t represents the time (in years) since the study began. When t = 0, it refers to the starting point of the study.
2. Initial value in exponential functions: In exponential functions, the value of the population (or quantity) at t = 0 is always the constant factor outside the parentheses (in this case, 1,800). This is the initial amount before growth or decay starts.
3. Application to real-world context: Here, P(0) = 1,800 reflects the number of marine mammals at the very beginning of the study.

Step-by-Step Solution
Step 1: Understand the function
The function P(t) = 1,800(1.02)^t is an exponential growth model. Here:
~ 1,800 is the initial population of marine mammals.
~ 1.02 is the growth factor, representing a 2% increase each year (since 1.02 = 1 + 0.02).
~ t represents the number of years since the study began.
Step 2: Interpret P(0)
To interpret P(0) = 1,800, substitute t = 0 into the function:
P(t) = 1,800(1.02)^t
P(t) = 1,800(1.02)⁰
Step 3: Simplify the calculation
Using the property of exponents, (1.02)⁰ = 1:
P(0) = 1,800 x 1 = 1,800
This means that at the beginning of the study (when t = 0), the population of marine mammals was 1,800.

Question: A manager is responsible for ordering supplies for a shaved ice shop. The shop’s inventory starts with 4,500 paper cups and the manager estimates that 70 of these paper cups are used each day. Based on this estimate, in how many days will the supply of paper cups reach 1,700?
A) 20
B) 40
C) 60
D) 80

Choice B is correct. It’s given that the shop’s inventory starts with 4,500 paper cups and that the manager estimates that 70 of these paper cups are used each day. Let x represent the number of days in which the estimated supply of paper cups will reach 1,700. The equation 4,500 – 70x = 1,700 represents this situation. Subtracting 4,500 from both sides of this equation yields -70x = -2,800.
Dividing both sides of this equation by -70 yields x = 40. Therefore, based on this estimate, the supply of paper cups will reach 1,700 in 40 days.

Choice A is incorrect. After 20 days, the estimated supply of paper cups would be 4,500 – 70(20), or 3,100 cups, not 1,700 cups.

Choice C is incorrect. After 60 days, the estimated supply of paper cups would be 4,500 – 70(60), or 300 cups, not 1,700 cups.

Choice D is incorrect. After 80 days, the estimated supply of paper cups would be 4,500 – 70(80), or -1,100 cups, which isn’t possible.

The question asks you to find days of inventory cups (4500) reaching 1700. We know, people consume 70 every day, so 4500 – 70x = 1700. Since you have the advantage of using a calculator, why not use it then? Just multiply options one by one with 70 then subtract with 4500.
Here, 4500 – 70 x 40
4500 – 2800 = 1700.
OR
Explanation of the Process
Understand the problem: The inventory decreases linearly over time, meaning the rate of cup usage (70/day) is constant.
Set up a linear equation: Use the given quantities and rate of usage to form an equation.
Solve for the unknown: Isolate t to determine the time it will take to reach the target inventory.

Step-by-Step Solution
Step 1: Identify the situation
The problem involves the initial quantity of cups, a rate of decrease per day, and the final quantity of cups. This is a linear relationship because the number of cups decreases at a constant rate.
~ Initial quantity of cups: 4,500
~ Final quantity of cups: 1,700
~ Rate of usage per day: 70 cups/day
We are looking for the number of days (t) it will take to reduce the inventory to 1,700 cups.
Step 2: Set up the equation
The inventory decreases linearly over time, which can be expressed as: Final inventory = Initial inventory − (rate of usage × t)
Substitute the known values into the equation: 1,700 = 4,500 − 70t

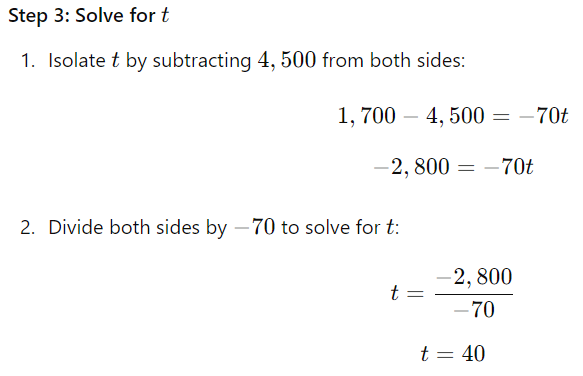
Step 4: Verify the solution
After 40 days, the total cups used would be: 70 × 40 = 2,800 cups.
Starting with 4,500 cups, the remaining inventory is: 4,500 − 2,800 = 1,700 cups.
The solution is correct: it will take 40 days.

Question:

A) 810
B) 1,20,000
C) 60,000
D) 410
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

Choice D:

Choice A is incorrect and may result from conceptual or calculation errors.

Choice B is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

Explanation of the Process
1. Understand the doubling condition: Doubling means the final population is twice the initial population.
2. Set up the equation: Use the function f(t) and substitute the condition f(t) = 120,000.
3. Simplify the exponential equation: Divide to isolate the exponential term and apply logarithmic rules (or direct comparison of exponents when the bases match).
4. Solve for the unknown t: Use algebraic techniques to find the time.

Step-by-Step Solution
Step 1: Understand the doubling condition
The initial population of bacteria is 60,000. For the population to double, the number of bacteria must be: 2 × 60,000 = 120,000
This means we need to solve for t in the equation: f(t) = 120,000
Step 2: Set up the equation
Substitute f(t) = 120,000 into the given function: 120,000 = 60,000(2)^{t / 410​}

It takes 410 minutes for the bacteria population to double. (Because if you divide 410 into 410, you will get 1, that is the power of (2)¹.

Question: The function f is defined by f(x) = (x − 6)(x − 2)(x + 6). In the xy-plane, the graph of y = g(x) is the result of translating the graph of y = f(x) up 4 units. What is the value of g(0)?
A) 0
B) 72
C) 76
D) 288
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

Choice C: The correct answer is 76. It’s given that the graph of y = g(x) is the result of translating the graph of y = f(x) = up 4 units in the xy-plane. It follows that the graph of y = g(x) is the same as the graph of y = f(x) + 4. Substituting g(x) for y in the equation y = f(x) + 4 yields g(x) = f(x) + 4. It’s given that f(x) = (x – 6)(x -2)(x + 6). Substituting (x – 6)(x -2)(x + 6) for f(x) in the equation g(x) = f(x) + 4 yields g(x) = (x – 6)(x – 2)(x + 6) + 4. Substituting 0 for x in this equation yields g(0) = (0 – 6)(0 – 2)(0 + 6) + 4, or g(0) = 76. Thus, the value of g(0) is 76.

Choice A is incorrect and may result from conceptual or calculation errors.

Choice B is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

Step-by-step Solution:
1. Understand the relationship between g(x) and f(x):
Translating a graph up by 4 units means adding 4 to the output of the original function f(x).
Mathematically, this is expressed as: g(x) = f(x) + 4
Here, g(x) is the new function after translating the graph.
2. Interpret the Problem’s Requirements:
The question asks for g(0), i.e., the value of g(x) when x = 0.
Using the relationship g(x) = f(x) + 4, we know that: g(0) = f(0) + 4
So, the first step is to compute f(0).
3. Substitute x = 0 into f(x):
~ The function f(x) = (x − 6)(x − 2)(x + 6) is given.
~ Compute f(0): f(0) = (0 − 6)(0 − 2)(0 + 6)
~ Simplify the terms inside the parentheses: f(0) = (−6)(−2)(6)
~ Multiply the terms: f(0) = 72
[When we multiply two negatives, it becomes positive (-6 x -2).]
4. Use the relationship between g(x) and f(x):
~ Since g(x) = f(x)+4, substitute f(0) into this equation to find g(0): g(0) = f(0) + 4
~ Substitute f(0) = 72: g(0) = 72 + 4 = 76 Answer

Question: A candle is made of 17 ounces of wax. When the candle is burning, the amount of wax in the candle decreases by 1 ounce every 4 hours. If 6 ounces of wax remains in this candle, for how many hours has it been burning?
A) 3
B) 6
C) 24
D) 44

Choice D is correct. It’s given that the candle starts with 17 ounces of wax and has 6 ounces of wax remaining after a period of time has passed. The amount of wax the candle has lost during the time period can be found by subtracting the remaining amount of wax from the amount of wax the candle was made of, which yields 17-6 ounces, or 11 ounces. This means the candle loses 11 ounces of wax during that period of time. It’s given that the amount of wax decreases by 1 ounce every 4 hours. If h represents the number of hours the candle has been burning, it follows that ¹/₄ = ¹¹/_h. Multiplying both sides of this equation by 4h yields 44h=. Therefore, the candle has been burning for 44 hours.

Choice A is incorrect and may result from using the equation ¹/₄ = ^h/₁₁ rather than ¹/₄ = ¹¹/_h to represent the situation, and then rounding to the nearest whole number.

Choice B is incorrect. This is the amount of wax, in ounces, remaining in the candle, not the number of hours it has been burning.

Choice C is incorrect and may result from using the equation ¹/₄ = ⁶/_h rather than ¹/₄ = ¹¹/_h to represent the situation.

Step-by-Step Explanation:
Step 1: Understand the problem
We are tasked with calculating how long the candle has been burning given:
~ The initial amount of wax: 17 ounces
~ The final amount of wax: 6 ounces
~ The rate of burning: 1 ounce every 4 hours
We need to find the time t (in hours) that it took for the candle to burn from 17 ounces to 6 ounces.
Step 2: Set up the equation
1. Determine the total amount of wax burned:
~ The candle starts with 17 ounces and ends with 6 ounces.
~ The amount of wax burned is:
Wax burned = 17 − 6 = 11 ounces
2. Relate the amount of wax burned to the time it has burned:
~ The candle burns 1 ounce every 4 hours. Therefore, the total time it takes to burn 11 ounces can be calculated using the relationship:
Time = Wax burned × Time per ounce burned
~ Since the candle burns 1 ounce every 4 hours, the time per ounce burned is 4 hours/ounce. Substitute:
Time = 11 ounces × 4 hours/ounce
Step 3: Perform the calculation
Time = 11 × 4 = 44 hours
Step 4: Verify the result
~ If the candle burns 1 ounce every 4 hours, then in 44 hours it burns:
44 / 4 = 11 ounces (44 is divided by 4)
~ Starting from 17 ounces, after burning 11 ounces, 6 ounces remain:
17 − 11 = 6 ounces

Question: The function f(x) = 206(1.034)^x models the value, in dollars, of a certain bank account by the end of each year from 1957 through 1972, where x is the number of years after 1957. Which of the following is the best interpretation of “f(5) is approximately equal to 243” in this context?
A) The value of the bank account is estimated to be approximately 5 dollars greater in 1962 than in 1957.
B) The value of the bank account is estimated to be approximately 243 dollars in 1962.
C) The value, in dollars, of the bank account is estimated to be approximately 5 times greater in 1962 than in 1957.
D) The value of the bank account is estimated to increase by approximately 243 dollars every 5 years between 1957 and 1972.

Choice B is correct. It’s given that the function f(x) = 206(1.034)^x models the value, in dollars, of a certain bank account by the end of each year from 1957 through 1972, where x is the number of years after 1957. It follows that f(x) represents the estimated value, in dollars, of the bank account x years after 1957. Since the value of f(5) is the value of f(x) when x = 5, it follows that “f(5) is approximately equal to 243” means that f(x) is approximately equal to 243 when x =5. In the given context, this means that the value of the bank account is estimated to be approximately 243 dollars 5 years after 1957. Therefore, the best interpretation of the statement “f(5) is approximately equal to 243” in this
context is the value of the bank account is estimated to be approximately 243 dollars in 1962.

Choice A is incorrect and may result from conceptual errors.

Choice C is incorrect and may result from conceptual errors.

Choice D is incorrect and may result from conceptual errors.

Step-by-Step Explanation:
Step 1: Understand the function
1. Initial value:
The value 206 represents the amount in the bank account in 1957 when x=0. Thus, f(0) = 206.
2. Growth rate:
The term (1.034)^x represents the annual growth of the account. The base, 1.034, indicates a 3.4% annual increase in the account’s value.
3. Input x:
The variable x represents the number of years after 1957. For example:
~ x = 0: The year 1957
~ x = 5: The year 1962
~ x = 15: The year 1972

Step 2: Interpret f(5) ≈ 243
1. f(5) represents the value of the bank account 5 years after 1957. This corresponds to the year: 1957 + 5 = 1962
2. f(5) ≈ .243 means the value of the account in 1962 is approximately $243. (Answer)

Why Each Step Was Performed:
1. Analyze the structure of the function:
Understanding the components of f(x) = 206(1.034)^x helps identify the meaning of the initial value (206), the growth rate (1.034), and how x relates to time (years after 1957).
2. Substitute x = 5:
This step associates the input x = 5 with the year 1962 and calculates the value of the account at that specific time.
3. Interpret the approximate output:
Connecting f(5) ≈ 243 to real-world terms clarifies that it refers to the account’s value in 1962.

Question: Square P has a side length of x inches. Square Q has a perimeter that is 176 inches greater than the perimeter of square P. The function f gives the area of square Q, in square inches. Which of the following defines f ?
A) f(x) = (x + 44)²
B) f(x) = (x + 176)²
C) f(x) = (176x + 44)²
D) f(x) = (176x + 176)²

Choice B is correct. It’s given that the ratio of the rectangular region’s length to its
width is 35 to 10.

This proportion can be rewritten as 10l = 35w, or l = 3.5w. If the width of the rectangular region increases by 7, then the length will increase by some number x in order to maintain this ratio. The value of x can be found by replacing l with l + x and w with w + 7 in the equation, which gives l + x = 3.5(w + 7). This equation can be rewritten using the distributive property as l + x = 3.5w + 24.5. Since l = 3.5w, the right-hand side of this equation can be rewritten by substituting l for 3.5w, which gives l + x = l + 24.5, or x = 24.5. Therefore, if the width of the rectangular region increases by 7 units, the length must increase by 24.5 units in order to maintain the given ratio.

Choice A is incorrect. If the width of the rectangular region increases, the length must also increase, not decrease.

Choice C is incorrect. If the width of the rectangular region increases, the length must also increase, not decrease.

Choice D is incorrect. Since the ratio of the length to the width of the rectangular region is 35 to 10, if the width of the rectangular region increases by 7 units, the length would have to increase by a proportional amount, which would have to be greater than 7 units.

Step-by-Step Explanation:

Step 2: Write the function for the area of square Q
The area of a square is calculated as:
~ Area = (side length)²
~ For square Q, the side length is x + 44. Therefore, the area of square Q is:
Area of square Q = (x + 44)²
~ Define the function f(x) to represent the area of square Q:
f(x) = (x+44)².

Step 3: Expand the function for clarity (optional)
If expanded, f(x) becomes:
f(x) = (x + 44)² = x² + 88x + 1936.
However, leaving f(x) in factored form, (x+44)², is often more concise and interpretable in context.

Why Each Step Was Performed:
1. Calculate the perimeter of square Q:
The problem explicitly states the relationship between the perimeters of squares P and Q. This step ensures the side length of Q is correctly derived.
2. Express the area in terms of the side length:
The area of square Q depends on its side length, which is expressed in terms of x. This step relates the dimensions of Q back to x.
3. Formulate the function f(x):
Translating the area calculation into function form connects the problem’s variables with the output (area of square Q).

Question:

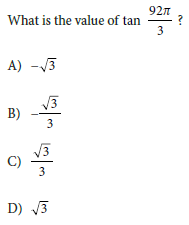
Choice A is correct. A trigonometric ratio can be found using the unit circle, that is, a circle with a radius of 1 unit. If a central angle of a unit circle in the xy-plane centered at the origin has its starting side on the positive x-axis and its terminal side intersects the circle at a point (x, y), then the value of the tangent of the central angle is equal to the y-coordinate divided by the x-coordinate. There are

Choice B is incorrect.

Choice C is incorrect.

Choice D is incorrect.

Step-by-Step Explanation:

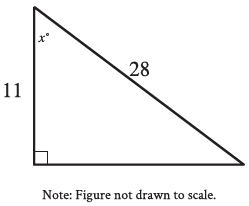
Question: In the triangle shown, what is the value of cos x°?
A) 810
B) 1,20,000
C) 60,000
D) 410
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

Choice A: The correct answer is 11/28. The cosine of an acute angle in a right triangle is defined as the ratio of the length of the leg adjacent to the angle to the length of the hypotenuse. In the triangle shown, the length of the leg adjacent to the angle with measure x° is 11 units and the length of the hypotenuse is 28 units. Therefore, he value of cos x° is 11/28.

[Note that 11/28, .3928, .3929, 0.392, and 0.393 are examples of ways to enter a correct answer.]

Choice B is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

Step-by-Step Explanation:
Step 1: Understand what cosine (cos⁡) means
In a right triangle, the cosine of an angle is defined as:

11/28 is the answer.

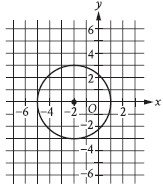
Question: Circle A (shown) is defined by the equation (x + 2)² + y² = 9. Circle B (not shown) is the result of shifting circle A down 6 units and increasing the radius so that the radius of circle B is 2 times the radius of circle A. Which equation defines circle B?
A) (x + 2)² + (y + 6)² = (4)(9)
B) 2(x + 2)² + 2(y + 6)² = 9
C) (x + 2)² + (y − 6)² = (4)(9)
D) 2(x + 2)² + 2(y − 6)² = 9

Choice A is correct. According to the graph, the center of circle A has coordinates (-2, 0), and the radius of circle A is 3. It’s given that circle B is the result of shifting circle A down 6 units and increasing the radius so that the radius of circle B is 2 times the radius of circle A. It follows that the center of circle B is 6 units below the center of circle A. The point that’s 6 units below (-2, 0) has the same x-coordinate as (-2, 0) and has a y-coordinate that is 6 less than the y-coordinate of (-2, 0). Therefore, the coordinates of the center of circle B are (-2, 0 – 6), or (-2,-6). Since the radius of circle B is 2 times the radius of circle A, the radius of circle B is (2)(3). A circle in the xy-plane can be defined by an equation of the form (x – h)² + (y – k)² = r², where the coordinates of the center of the circle are (h, k) and the radius of the circle is r. Substituting -2 for h, -6 for k, and (2)(3) for r in this equation yields
(x – (-2))² + (y – (-6))² = ((2)(3))², which is equivalent to (x + 2)² + (y + 6)² = (2)²(3)² or (x + 2)² + (y + 6)² = (4)(9). Therefore, the equation (x + 2)² + (y + 6)² = (4)(9) defines circle B.

Choice B is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect. This equation defines a circle resulting from shifting circle A up, not down, by 6 units and increasing the radius.

Choice D is incorrect and may result from conceptual or calculation errors.

Step 1: Analyze Circle A’s Equation
The given equation for Circle A is: (x+2)² + y² = 9
From the standard equation of a circle: (x−h)² + (y−k)² = r²
~ (h, k): The center of the circle.
~ r: The radius of the circle.

For Circle A:
~ Center: (−2, 0) (from x + 2 = 0 and y² = 0).
~ Radius: r = square root of 9 is 3.

Step 2: Describe the Transformations
1. Shift Circle A Down by 6 Units:
~ Shifting down by 6 units affects the y-coordinate of the center.
~ The new center of Circle B becomes: (−2, 0 − 6) = (−2, −6).
2. Double the Radius:
~ Circle B’s radius is twice that of Circle A: r_B = 2 × 3 = 6.

Step 3: Write Circle B‘s Equation
Using the standard form of a circle, substitute the new center (−2, −6) and radius r_B = 6:
(x + 2)² +(y + 6)² = 6²
(x + 2)² + (y + 6)² = 36

Step 4: Compare with the Options
The equation matches Option A: (x + 2)² + (y + 6)² = (4)(9)
since 6² = 36 = 4 ⋅ 9 (It means 4 x 9, 4 multiply by 9 is 36.)

Question:

Choice C:

Choice A is incorrect and may result from conceptual or calculation errors.

Choice B is incorrect and may result from conceptual or calculation errors.

Choice D is incorrect and may result from conceptual or calculation errors.

Problem Explanation:

Step-by-Step Solution:

Question: At the time that an article was first featured on the home page of a news website, there were 40 comments on the article. An exponential model estimates that at the end of each hour after the article was first featured on the home page, the number of comments on the article had increased by 190% of the number of comments on the article at the end of the previous hour. Which of the following equations best represents this model, where C is the estimated number of comments on the article t hours after the article was first featured on the home page and t ≤ 4 ?
A) C = 40(1.19)^t
B) C = 40(1.9)^t
C) C = 40(19)^t
D) C = 40(2.9)^t

Choice D is correct. It’s given that an exponential model estimates that the number of comments on an article increased by a fixed percentage at the end of each hour. Therefore, the model can be represented by an exponential equation of the form C = Ka^t, where C is the estimated number of comments on the article t hours after the article was first featured on the home page and K and a are
constants. It’s also given that when the article was first featured on the home page of the news website, there were 40 comments on the article. This means that when t = 0, C = 40. Substituting 0 for t and 40 for C in the equation C = Ka^t yields 40 = Ka⁰, or 40 = K. It’s also given that the number of comments on the article at the end of an hour had increased by 190% of the number of comments
on the article at the end of the previous hour. Multiplying the percent increase by the number of comments on the article at the end of the previous hour yields the number of estimated additional comments the article has on its home page: (40)(190/100), or 76 comments. Thus, the estimated number of comments for the following hour is the sum of the comments from the end of the previous hour and the number of additional comments, which is 40 + 76, or 116. This means that when t = 1, C = 116. Substituting 1 for t, 116 for C, and 40 for K in the equation C = Ka^t yields 116 = 40a¹, or 116 = 40a. Dividing both sides of this equation by 40 yields 2.9 = a. Substituting 40 for K and 2.9 for a in the equation C = Ka^t yields C = 40(2.9)^t. Thus, the equation that best represents this model is C = 40(2.9)^t.

Choice A is incorrect. This model represents a situation where the number of comments at the end of each hour increased by 19% of the number of comments at the end of the previous hour, rather than 190%.

Choice B is incorrect. This model represents a situation where the number of comments at the end of each hour increased by 90% of the number of comments at the end of the previous hour, rather than 190%.

Choice C is incorrect. This model represents a situation where the number of comments at the end of each hour was 19 times the number of comments at the end of the previous hour, rather than increasing by 190% of the number of comments at the end of the previous hour.

Step-by-Step Solution:
1. Understanding Exponential Growth:
Exponential growth occurs when the rate of growth is proportional to the current amount. In this case:
~ At the end of every hour, the number of comments increases by 190% of the current number of comments.
~ 190% growth means the new total at the end of each hour is 290% of the previous total (100% original + 190% increase).

2. Formulating the Growth Factor:
The growth factor, r, represents how much the number of comments grows in one-time unit. Here: r = 1 + 1.9 = 2.9
~ This is because the number of comments increases by 190%, making the total 290% of the previous amount.

3. General Exponential Growth Formula:
The formula for exponential growth is: C(t) = C₀ ⋅ r^t
Where:
~ C(t): Number of comments at time t.
~ C₀​: Initial number of comments (when t = 0).
~ r: Growth factor.
~ t: Time in hours.

4. Substituting Known Values:
~ Initial number of comments: C₀ = 40,
~ Growth factor: r = 2.9,
~ Time: t ≤ 4.
Thus, the equation becomes: C(t) = 40 ⋅ (2.9)^t

Explanation of the Model:
1. At t = 0, the article has exactly 40 comments: C(0) = 40 ⋅ (2.9)⁰
2. After 1 hour (t = 1), the number of comments grows by 190%:
C(1) = 40 ⋅ (2.9)¹ = 40 ⋅ 2.9 = 116
This matches the exponential growth pattern.
3. After 2 hours (t = 2): C(2) = 40 ⋅ (2.9)² ≈ 40 ⋅ 8.41 = 336.4
The number of comments has grown significantly.
4. The same logic applies for t = 3 and t = 4.

The best equation to model this situation is: C(t) = 40 ⋅ (2.9)^t​

(This ⋅ means multiply: 2 ⋅ 2 OR 2 x 2 = 4.)

Question:

A) (0, 36)
B) (0, 12)
C) (0, 4)
D) (0, -9)

Choice A:

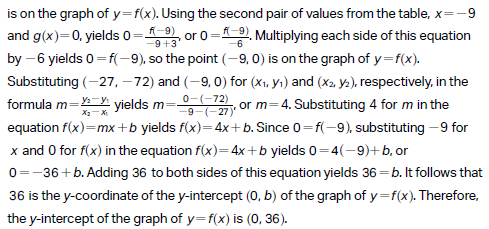
Choice B is incorrect. 12 is the y-coordinate of the y-intercept of the graph of y = g(x).

Choice C is incorrect. 4 is the slope of the graph of y = f(x).

Choice D is incorrect. -9 is the x-coordinate of the x-intercept of the graph of y = f(x).

Step-by-Step Solution:

4. Find the equation of f(x):
The general equation of a line is: f(x) = mx + b
Substituting m = 4 and using the point (−9, 0) to solve for b:
0 = 4(−9) + b
0 = −36 + b
b = 36
Thus, the equation of f(x) is: f(x) = 4x + 36
5. Find the y-intercept of f(x):
The y-intercept occurs when x = 0. Substituting x = 0 into f(x) = 4x + 36: f(0) = 4(0) + 36 = 36
Therefore, the y-intercept of f(x) is 36.

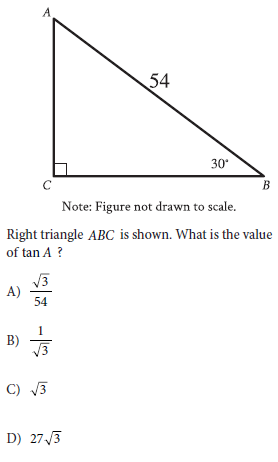
Question: In the right triangle ABC, angle C is the right angle and BC = 162. Point D on side AB is connected by a line segment with point E on side AC such that line segment DE is parallel to side BC and CE = 2AE. What is the length of line segment DE ?
A) 18
B) 84
C) 24
D) 54
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]

Choice D: The correct answer is 54. It’s given that in triangle ABC, point D on side AB is connected by a line segment with point E on side AC such that line segment DE is parallel to side BC. It follows that parallel segments DE and BC are intersected by sides AB and AC. If two parallel segments are intersected by a third segment, corresponding angles are congruent. Thus, corresponding angles C and AED are congruent and corresponding angles B and ADE are congruent. Since triangle ADE has two angles that are each congruent to an angle in triangle ABC, triangle ADE is similar to triangle ABC by the angle-angle similarity postulate, where side DE corresponds to side BC, and side AE corresponds to side AC.

Choice A is incorrect and may result from conceptual or calculation errors.

Choice B is incorrect and may result from conceptual or calculation errors.

Choice C is incorrect and may result from conceptual or calculation errors.

Problem Restatement:
In the right triangle △ABC:
~ Angle C is a right angle, and BC = 162.
~ A point D lies on side AB, and point E lies on side AC, forming a line segment DE parallel to BC.
~ The ratio CE : AE = 2 : 1.
We are tasked with finding the length of DE, given that it is parallel to BC.

Step-by-Step Solution: