
Master the SAT Test of Math Module 2nd with Tricks to Achieve 1500 Marks
Did you find the SAT Math complex? If yes, then you are in the right place. We have designed a similar exam format with all the necessary features for you to become a master in Math. You take the SAT Test Module Second to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 2nd.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 2ND
The second module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 2nd are only difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 2nd. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH STUDY GUIDE AND PROBLEM SOLUTIONS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: The line graph shows the estimated number of chipmunks in a state park on April 1 of each year from 1989 to 1999.
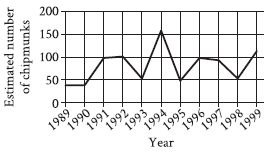
Based on the line graph, in which year was the estimated number of chipmunks in the state park the greatest?
A) 1989
B) 1994
C) 1995
D) 1998
Choice B is correct. For the given line graph, the estimated number of chipmunks is represented on the vertical axis. The greatest estimated number of chipmunks in the state park is indicated by the greatest height in the line graph. This height is achieved when the year is 1994.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
We are tasked with identifying the year in which the estimated number of chipmunks in a state park was the greatest, based on the provided line graph.
Step 1: Understand the question and analyze the graph
The line graph shows:
~ The horizontal axis (x-axis): Represents the year from 1989 to 1999.
~ The vertical axis (y-axis): Represents the estimated number of chipmunks.
The question asks for the year where the highest point on the graph occurs, which corresponds to the greatest number of chipmunks.
Step 2: Locate the peak on the graph
1) Observe the graph closely:
~ The highest point on the graph represents the maximum value on the y-axis.
~ Follow the y-values for each year and find the tallest peak.
2) Identify the year corresponding to the highest point:
~ The highest point occurs at 1994, where the estimated number of chipmunks is approximately 150.
Step 3: Confirm the highest value
~ The y-value in 1994 reaches the maximum point on the graph, and no other year has a higher or equal number.
~ The highest estimated number of chipmunks in 1994 is clearly greater than the numbers for all other years.
Final Answer:
The estimated number of chipmunks in the state park was the greatest in: 1994.
2nd Question
Question: A fish swam a distance of 5,104 yards. How far did the fish swim, in miles? (1 mile = 1,760 yards)
A) 0.3
B) 2.9
C) 3,344
D) 6,864
Choice B is correct. It’s given that the fish swam 5,104 yards and that 1 mile is equal to 1,760 yards. Therefore, the fish swam 5,104 yards(1 mile/1,760 yards), which is equivalent to 5,104/1,760 miles, or 2.9 miles.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution
We are tasked with converting the distance a fish swam, given in yards, to miles.
1) Given Information:
The fish swam 5,104 yards.
2) Conversion factor: 1 mile = 1,760 yards.
Step 1: Set up the conversion
To convert yards to miles, divide the total distance in yards by the number of yards in one mile.
Distance in miles = Distance in yards/Yards per mile
Substitute the given values:
Distance in miles = 5,104/1,760
Step 2: Perform the division
Divide 5,104 by 1,760:
5,104 ÷ 1,760 = 2.9 miles
Step 3: Verify the result
1) Multiply 2.9 miles by 1,760 yards/mile, to ensure it equals 5,104 yards:
2.9 × 1,760 = 5,104 yards
The calculation checks out.
Final Answer: The fish swam 2.9 miles.
3rd Question
Question: Which expression is equivalent to 12x3 − 5x3?
A) 7x6
B) 17x3
C) 7x3
D) 17x6
Choice C is correct. The given expression shows subtraction of two like terms. The two terms can be subtracted as follows: 12x3 – 5x3 = (12 – 5)x3, or 7x3.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect. This is the result of adding, not subtracting, the two-like terms.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Identify the terms
~ Both terms have the same variable part, x3, which means they are like terms.
~ The coefficients of the terms are 12 and −5.
Step 2: Combine like terms
To simplify 12x3 − 5x3, subtract the coefficients of the like terms while keeping the variable part x3 unchanged:
12x3 − 5x3 = (12 − 5)x3
Step 3: Perform the subtraction
Subtract 5 from 12:
12 − 5 = 7
Thus, the simplified expression is:
7x3
Verification:
~ Combine like terms: 12x3 and −5x3 simplify directly to 7x3.
~ No further simplification is possible since there are no additional like terms or operations.
Final Answer: The expression equivalent to 12x3 − 5x3 is: 7x3.
4th Question
x + y = 18
5y = x
Question: What is the solution (x, y) to the given system of equations?
A) (15, 3)
B) (16, 2)
C) (17, 1)
D) (18, 0)
Choice A is correct. The second equation in the given system defines the value of x as 5y. Substituting 5y for x into the first equation yields 5y + y = 18 or 6y = 18. Dividing each side of this equation by 6 yields y = 3. Substituting 3 for y in the second equation yields 5(3) = x or x = 15. Therefore, the solution (x, y) to the given system of equations is (15, 3).
Choice B is incorrect. Substituting 16 for x and 2 for y in the second equation yields 5(2) = 16, which is not true. Therefore, (16, 2) is not a solution to the given system of equations.
Choice C is incorrect. Substituting 17 for x and 1 for y in the second equation yields 5(1) = 17, which is not true. Therefore, (17, 1) is no a solution to the given system of equations.
Choice D is incorrect. Substituting 18 for x and 0 for y in the second equation yields 5(0) = 18, which is not true. Therefore, (18, 0) is not a solution to the given system of equations.
Step-by-Step Solution:
Step 1: Solve one equation for one variable
From the second equation: 5y = x
We can rewrite x in terms of y: x = 5y
Step 2: Substitute into the first equation
Substitute x = 5y into the first equation x + y = 18:
5y + y = 18
Step 3: Combine like terms
Combine the terms involving y: 6y = 18
Step 4: Solve for y
Divide both sides of the equation by 6:
y = 18/6 = 3
Step 5: Solve for x
Now that y = 3, substitute this value back into the equation x = 5y:
x = 5(3) = 15
Verification:
1) Substitute x = 15 and y = 3 into the first equation x + y = 18:
15 + 3 = 18 (True)
2) Substitute x = 15 and y = 3 into the second equation 5y = x:
5(3) = 15 (True)
Thus, the solution is verified as correct.
Final Answer: The solution to the system of equations is: (x, y) = (15, 3).
5th Question
Question: The point (8, 2) in the xy-plane is a solution to which of the following systems of inequalities?
A) x > 0, y > 0
B) x > 0, y < 0
C) x < 0, y > 0
D) x < 0, y < 0
Choice A is correct. The given point, (8, 2), is located in the first quadrant in the xy-plane. The system of inequalities in choice A represents all the points in the first quadrant in the xy-plane. Therefore, (8, 2) is a solution to the system of inequalities in choice A.
Alternate approach: Substituting 8 for x in the first inequality in choice A, x > 0, yields 8 > 0, which is true. Substituting 2 for y in the second inequality in choice A, y > 0, yields 2 > 0, which is true. Since the coordinates of the point (8, 2) make the inequalities x >0 and y >0 true, the point (8, 2) is a solution to the system of inequalities consisting of x > 0 and y > 0.
Choice B is incorrect. This system of inequalities represents all the points in the fourth quadrant, not the first quadrant, in the xy-plane.
Choice C is incorrect. This system of inequalities represents all the points in the second quadrant, not the first quadrant, in the xy-plane.
Choice D is incorrect. This system of inequalities represents all the points in the third quadrant, not the first quadrant, in the xy-plane.
Step-by-Step Solution:
Step 1: Analyze the given point (8,2)
The point (8, 2) has:
x = 8, which is positive (x > 0),
y = 2, which is positive (y > 0).
Step 2: Test the point against each system of inequalities
We will check whether the point (8, 2) satisfies each inequality system:
1) Option A: x > 0, y > 0
x = 8 > 0: True
y = 2 > 0: True
Result: The point satisfies both inequalities.
2) Option B: x > 0, y < 0
x = 8 > 0: True
y = 2 < 0: False
Result: The point does not satisfy this system.
3) Option C: x < 0, y > 0
x = 8 < 0: False
y = 2 > 0: True
Result: The point does not satisfy this system.
4) Option D: x < 0, y < 0
x = 8 < 0: False
y = 2 < 0: False
Result: The point does not satisfy this system.
Step 3: Identify the correct system of inequalities
From the above analysis, only Option A: x > 0, y > 0 is satisfied by the point (8, 2).
Final Answer: The correct answer is: A) x > 0, y > 0.
6th Question
x = 8
x + 3y = 26
Question: The solution to the given system of equations is (x, y). What is the value of y?
A) 3
B) 6
C) 18
D) 24
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B: The correct answer is 6. The first equation in the given system is x = 8. Substituting 8 for x in the second equation in the given system yields 8 + 3y = 26. Subtracting 8 from both sides of this equation yields 3y = 18. Dividing both sides of this equation by 3 yields y = 6. Therefore, the value of y is 6.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Substitution
From the first equation, x = 8.
Substitute x = 8 into the second equation, x + 3y = 26, to eliminate x.
8 + 3y = 26
Step 2: Simplify the equation
Solve for y by isolating it on one side of the equation:
3y = 26 − 8
3y = 18
Step 3: Solve for y
Divide both sides of the equation by 3:
y = 18/3
y = 6
Step 4: Verify the solution
Substitute x = 8 and y = 6 into both equations to confirm the solution:
1) From the first equation: x = 8: True.
2) From the second equation:
x + 3y = 26:
8 + 3(6) = 26:
8 + 18 = 26:
26 = 26: True.
The solution (x, y) = (8, 6) is correct.
Final Answer: The value of y is: 6.
7th Question
Question: The amount of Hanna’s bill for a food order was $50. Hanna gave a tip of 20% of the amount of the bill. What is the amount, in dollars, of the tip Hanna gave?
A) $5
B) $10
C) $20
D) $50
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B: The correct answer is 10. It’s given that the amount of Hanna’s food order was $50 and that Hanna gave a tip of 20% of the amount of the bill. 20% of 50 can be calculated as (20/100)(50), which yields 1000/100, or 10. Therefore, the amount, in dollars, of the tip Hanna gave is 10.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Recall the formula to calculate a percentage
The formula to calculate a percentage of a value is:
Percentage Amount = Percent (in decimal form) × Original Amount
Step 2: Convert the percentage to decimal form
Hanna gives a 20% tip. To use it in the formula, convert the percentage to decimal form by dividing by 100:
20% = 20/100 = 0.2
Step 3: Substitute values into the formula
The original amount of the bill is $50, and the percentage in decimal form is 0.2. Substitute these into the formula:
Tip Amount = 0.2 × 50
Step 4: Perform the calculation
Tip Amount = 10
Step 5: Interpret the result
Hanna gave a tip of $10.
Final Answer: The tip Hanna gave is: $10.
8th Question
Question: Which expression is equivalent to 5x5 − 6x4 + 8x3?
A) x4(5x − 6)
B) x3(5x2 − 6x + 8)
C) 8x3(5x2 − 6x + 1)
D) 6x5(−6x4 + 8x3 + 1)
Choice B is correct. Since x3 is a common factor of each term in the given expression, the expression can be rewritten as x3(5x2 – 6x + 8).
Choice A is incorrect. This expression is equivalent to 5x5 – 6x4.
Choice C is incorrect. This expression is equivalent to 40x5 – 48x4 + 8x3.
Choice D is incorrect. This expression is equivalent to 36x9 + 48x8 + 6x5.
Step-by-Step Solution:
Step 1: Analyze the original expression
The given expression is:
5x5 − 6x4 + 8x3
The terms are already written in descending powers of x.
Step 2: Look for common factors
To factorize the expression, check if there is a common factor among all terms. Each term contains x3, so x3 can be factored out:
5x5 − 6x4 + 8x3 = x3(5x2 − 6x + 8)
Step 3: Match with the answer choices
Now we compare the factored form x3(5x2 − 6x + 8) with the provided options:
Choice A: x4(5x − 6)
Expand this: x4(5x − 6) = 5x5 − 6x4
This does not match the original expression because it is missing the 8x3 term. Choice A is incorrect.
Choice B: x3(5x2 − 6x + 8)
Expand this: x3(5x2 − 6x + 8) = 5x5 − 6x4 + 8x3
This matches the original expression exactly. Choice B is correct.
Choice C: 8x3(5x2 − 6x + 1)
Expand this: 8x3(5x2 − 6x + 1) = 40x5 − 48x4 + 8x3
This does not match the original expression because the coefficients are incorrect. Choice C is incorrect.
Choice D: 6x5(−6x4 + 8x3 + 1)
Expand this: 6x5(−6x4 + 8x3 + 1) = −36x9 + 48x8 + 6x5
This does not match the original expression because it introduces terms of a much higher degree than the original expression. Choice D is incorrect.
Final Answer: The correct choice is B: x3(5x2 − 6x + 8).
9th Question
Question: The ratio of the length of line segment XY to the length of line segment ZV is 6 to 1. If the length of line segment XY is 102 inches, what is the length, in inches, of line segment ZV?
A) 17
B) 96
C) 102
D) 612
Choice A is correct. It’s given that the ratio of the length of line segment XY to the length of line segment ZV is 6 to 1, which means XY/ZV = 6/1. It’s given that the length of line segment XY is 102 inches. If the length, in inches, of line segment ZV is represented by l, the value of l, can be calculated by solving the equation 102/l = 6/1, or 102/l = 6. Multiplying each side of this equation by l, yields 102 = 6l. Dividing each side of this equation by 6 yields 17 = l. Therefore, the length of line segment ZV is 17 inches.
Choice B is incorrect. This is the length, in inches, of line segment ZV if the length of line segment XY is 576, not 102, inches.
Choice C is incorrect. This is the length, in inches, of line segment XY, not line segment ZV.
Choice D is incorrect. This is the length, in inches, of line segment ZV if the ratio of the length of line segment XY to the length of line segment ZV is 1 to 6, not 6 to 1.
Problem Statement:
We are given:
~ The length of line segment XY is 102 inches. We need to find the length of line segment ZV.
~ The ratio of the lengths of line segments XY to ZV is 6 : 1.

Step 3: Verify the solution
To check, calculate the ratio of the lengths:
Length of XY/Length of ZV = 102/17 = 6,
which matches the given ratio of 6 : 1. Therefore, the solution is correct.
Final Answer: The length of line segment ZV is 17 inches.
10th Question
7(2x − 3) = 63
Question: Which equation has the same solution as the given equation?
A) 2x − 3 = 9
B) 2x − 3 = 56
C) 2x − 21 = 63
D) 2x − 21 = 70
Choice A is correct. Dividing each side of the given equation by 7 yields 7(2x – 3)/7 = 63/7, or 2x – 3 = 9. Therefore, the equation 2x – 3 = 9 is equivalent to the given equation and has the same solution.
Choice B is incorrect. This equation is equivalent to 7(2x – 3) = 392, not 7(2x – 3) = 63.
Choice C is incorrect. Distributing 7 on the left-hand side of the given equation yields 14x – 21 = 63, not 2x – 21= 63.
Choice D is incorrect. Distributing 7 on the left-hand side of the given equation yields 14x – 21 = 63, not 2x – 21 = 70.
Step-by-Step Solution:
Step 1: Simplify the given equation
Distribute 7 across the terms inside the parentheses:
7(2x − 3)
Expand: 7 ⋅ 2x − 7 ⋅ 3
14x − 21.
Thus, the equation becomes: 14x − 21 = 63.
Step 2: Find an equivalent equation
Divide both sides of the equation by 7 to simplify further:
7(2x − 3)/7
63/7
which simplifies to: 2x − 3 = 9.
This means the equation 2x − 3 = 9 has the same solution as the original equation.
Step 3: Verify the equivalence of all answer choices
Let’s check each answer choice by simplifying or comparing:
1) Choice A: 2x − 3 = 9
This matches the simplified form of the given equation, so it is correct.
2) Choice B: 2x − 3 = 56
This does not match because dividing 7(2x − 3) = 63 by 7 gives 2x − 3 = 9, not 56.
3) Choice C: 2x − 21 = 63
This does not match because the left-hand side 2x − 21 does not simplify to the original equation.
4) Choice D: 2x − 21 = 70
This is incorrect because the left-hand side 2x − 21 does not match the structure of the simplified equation 2x − 3 = 9.
Thus, the correct answer is Choice A: 2x − 3 = 9.
Final Answer: Choice A: 2x − 3 = 9.
11th Question
Question: Out of 300 seeds that were planted, 80% sprouted. How many of these seeds sprouted?
A) 340
B) 300
C) 260
D) 240
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D: The correct answer is 240. It’s given that 80% of the 300 seeds sprouted. Therefore, the number of seeds that sprouted can be calculated by multiplying the number of seeds that were planted by 80/100, which gives 300(80/100), or 240.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Understand the relationship
The percentage formula is given as:
Part = Percentage × Whole.
Here:
~ The whole is the total number of seeds planted, which is 300.
~ The percentage is 80%, or 0.80 in decimal form.
We need to calculate the part, which represents the number of seeds that sprouted.
Step 2: Plug in the values
Number of sprouted seeds = 0.80 × 300.
Step 3: Perform the multiplication
0.80 × 300 = 240.
Step 4: Verify the result
Rechecking the calculation:
~ 80% means 80 out of 100, or 0.80.
~ Multiplying 0.80 by 300 gives 240, confirming our result.
Final Answer: The number of seeds that sprouted is 240.
12th Question
Question: The function f is defined by f(x) = 4x. For what value of x does f(x) = 8?
A) 2
B) 4
C) 16
D) 32
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A: The correct answer is 2. Substituting 8 for f(x) in the given equation yields 8 = 4x. Dividing the left- and right-hand sides of this equation by 4 yields x = 2. Therefore, the value of x is 2 when f(x) = 8.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Understand the function
The function f(x) = 4x defines a relationship where any input x is multiplied by 4 to yield the output f(x).
Here, the goal is to find x when f(x) = 8.
Step 2: Set up the equation
From the problem, substitute f(x) = 8 into the equation:
4x = 8.
Step 3: Solve for x
Divide both sides of the equation by 4 to isolate x:
x = 8/4.
Simplify: x = 2.
Step 4: Verify the solution
To confirm, substitute x = 2 back into the function f(x) = 4x:
f(2) = 4 × 2 = 8.
The solution is verified as correct.
Final Answer: The value of x is 2.
13th Question
Question:
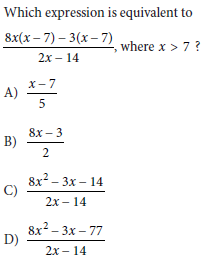
Choice B is correct.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Solution:
Step 1: Factorize the denominator
The denominator 2x − 14 can be factored:
2x − 14 = 2(x − 7).
Thus, the expression becomes:

Final Answer: B) 8x – 3/2
14th Question
Question: The minimum value of x is 12 less than 6 times another number n. Which inequality shows the possible values of x?
A) x ≤ 6n − 12
B) x ≥ 6n − 12
C) x ≤ 12 − 6n
D) x ≥12 − 6n
Choice B is correct. It’s given that the minimum value of x is 12 less than 6 times another number n. Therefore, the possible values of x are all greater than or equal to the value of 12 less than 6 times n. The value of 6 times n is given by the expression 6n. The value of 12 less than 6n is given by the expression 6n – 12. Therefore, the possible values of x are all greater than or equal to 6n – 12. This can be shown by the inequality x > 6n – 12.
Choice A is incorrect. This inequality shows the possible values of x if the maximum, not the minimum, value of x is 12 less than 6 times n.
Choice C is incorrect. This inequality shows the possible values of x if the maximum, not the minimum, value of x is 6 times n less than 12, not 12 less than 6 times n.
Choice D is incorrect. This inequality shows the possible values of x if the minimum value of x is 6 times n less than 12, not 12 less than 6 times n.
Problem Statement:
We are given that the minimum value of x is 12 less than 6 times another number n. We are tasked with finding the inequality that represents the possible values of x from the given options.
Step-by-Step Explanation:
Step 1: Translate the statement into an equation
The problem states:
“The minimum value of x is 12 less than 6 times n.”
1) 6 times n means 6n.
2) 12 less than 6 times n means: 6n − 12.
Thus, the minimum value of x is:
x ≥ 6n − 12.
This is because x can be greater than or equal to the minimum value.
Step 2: Verify the inequality
From the above reasoning, the inequality representing the possible values of x is:
x ≥ 6n − 12.
Step 3: Match with the options
The correct answer is: B) x ≥ 6n − 12.
15th Question
Question: Data set A consists of the heights of 75 buildings and has a mean of 32 meters. Data set B consists of the heights of 50 buildings and has a mean of 62 meters. Data set C consists of the heights of the 125 buildings from data sets A and B. What is the mean, in meters, of data set C?
A) 32
B) 44
C) 75
D) 100
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 44. The mean of a data set is computed by dividing the sum of the values in the data set by the number of values in the data set. It’s given that data set A consists of the heights of 75 buildings and has a mean of 32 meters. This can be represented by the equation x/75 = 32, where x represents the sum of the heights of the buildings, in meters, in data set A. Multiplying both sides of this equation by 75 yields x = 75(32), or x = 2,400 meters. Therefore, the sum of the heights of the buildings in data set A is 2,400 meters. It’s also given that data set B consists of the heights of 50 buildings and has a mean of 62 meters. This can be represented by the equation y/50 = 62, where y represents the sum of the heights of the buildings, in meters, in data set B. Multiplying both sides of this equation by 50 yields y = 50(62), or y = 3,100 meters. Therefore, the sum of the heights of the buildings in data set B is 3,100 meters. Since it’s given that data set C consists of the heights of the 125 buildings from data sets A and B, it follows that the mean of data set C is the sum of the heights of the buildings, in meters, in data sets A and B divided by the number of buildings represented in data sets A and B, or 2,400 + 3,100/125, which is equivalent to 44 meters. Therefore, the mean, in meters, of data set C is 44.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Statement:
We are tasked with finding the mean of data set C, which consists of the combined heights of 75 buildings in data set A (mean = 32 meters) and 50 buildings in data set B (mean = 62 meters).
Step-by-Step Explanation:
Step 1: Recall the formula for the mean
The mean of a data set is calculated as:
Mean = Sum of all values/Number of values.
For data set C, we need the total sum of the heights of all buildings and the total number of buildings.
Step 2: Calculate the total heights of buildings in each data set
1) For data set A:
~ Mean of A = 32.
~ Number of buildings in A = 75.
~ Total height of buildings in (A = 32 x 75 = 2400.)
2) For data set B:
~ Mean of B = 62.
~ Number of buildings in B = 50.
~ Total height of buildings in (B = 62 x 50 = 3100.)
Step 3: Calculate the total height and number of buildings in data set C
1) Total height of buildings in C:
Total height of C = Total height of A + Total height of B
2400 + 3100 = 5500 meters.
2) Total number of buildings in C:
Total number of buildings in C = Number of buildings in A + Number of buildings in B
75 + 50 = 125 buildings.
Step 4: Calculate the mean of data set C
The mean of C is given by:
Mean of C = Total height of C/Total number of buildings in C.
Substitute the values:
Mean of C = 5500/125 = 44 meters.
Final Answer: The mean of data set C is: 44 meters.
16th Question
Question:

A) 33
B) 44
C) 55
D) 66
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct. The correct answer is 66. It’s given that each vertex of the rectangle lies on the circumference of the circle. Therefore, the length of the diameter of the circle is equal to the length of the diagonal of the rectangle. The diagonal of a rectangle forms a right triangle with the shortest and longest sides of the rectangle, where the shortest side and the longest side of the rectangle are the legs of the triangle and the diagonal of the rectangle is the hypotenuse of the triangle. Let’s represent the length, in units, of the shortest side of the rectangle. Since it’s given that the diagonal is twice the length of the shortest side, 2s represents the length, in units, of the diagonal of the rectangle. By the Pythagorean theorem, if a right triangle has a hypotenuse with length c and legs with lengths a and b, then a2 + b2 = c2. Substituting s for a and 2s for c in this equation yields s2 + b2 = (2s)2, or s2 + b2 = 4s2. Subtracting s2 from both sides of this equation yields b2 = 3s2. Taking the positive square root of both sides of this equation yields b = s square root of 3. Therefore, the length, in units, of the rectangle’s longest side is s square root of 3. The area of a rectangle is the product of the length of the shortest side and the length of the longest side. The lengths, in units, of the shortest and longest sides of the rectangle are represented by s and s square root of 3, and it’s given that the area of the rectangle is 1,089 square root 3 square units. It follows that 1,089 square root 3 = s(s square root 3), or
1,089 square root 3 = s2 square root 3. Dividing both sides of this equation by square root 3 yields 1,089 = s2. Taking the positive square root of both sides of this equation yields 33 = s. Since the length, in units, of the diagonal is represented by 2s, it follows that the length, in units, of the diagonal is 2(33), or 66. Since the length of the diameter of the circle is equal to the length of the diagonal of the rectangle, the length, in units, of the diameter of the circle is 66.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
It looks complex but you can take advantage of the Desmos Calculator that you will get in the final exam.

Step 4: Find the diagonal of the rectangle
The diagonal of the rectangle is given as 2a:
Diagonal = 2a = 2 ⋅ 33 = 66.
Step 5: Relate the diagonal to the diameter of the circle
Since the rectangle is inscribed in the circle, the diagonal of the rectangle is equal to the diameter of the circle:
The diameter of the circle = 66.
Verification:
1) a = 33, b = 33 square root 3, and Diagonal = 66 satisfy all the given conditions:
~ Area = a ⋅ b = 33 ⋅ 33 square root 3 = 1,089 square root 3 (matches given area).
~ Diagonal = 2a = 66, which is consistent with the problem statement.
2) The circle’s diameter equals the rectangle’s diagonal, confirming that the solution is correct.
Final Answer: The diameter of the circle is: D) 66 units.
17th Question
Question: Rectangles ABCD and EFGH are similar. The length of each side of EFGH is 6 times the length of the corresponding side of ABCD. The area of ABCD is 54 square units. What is the area, in square units, of EFGH?
A) 9
B) 36
C) 324
D) 1,944
Choice D is correct. The area of a rectangle is given by bh, where b is the length of the base of the rectangle and h is its height. Let x represent the length, in units, of the base of rectangle ABCD, and let y represent its height, in units. Substituting x for b and y for h in the formula bh yields xy. Therefore, the area, in square units, of ABCD can be represented by the expression xy. It’s given that the length of each side of EFGH is 6 times the length of the corresponding side of ABCD. Therefore, the length, in units, of the base of EFGH can be represented by the expression 6x, and its height, in units, can be represented by the expression 6y. Substituting 6x for b and 6y for h in the formula bh yields (6x)(6y), which is equivalent to 36xy. Therefore, the area, in square units, of EFGH can be represented by the expression 36xy. It’s given that the area of ABCD is 54 square units. Since xy represents the area, in square units, of ABCD, substituting 54 for xy in the expression 36xy yields 36(54), or 1,944. Therefore, the area, in square units, of EFGH is 1,944.
Choice A is incorrect. This is the area of a rectangle where the length of each side of the rectangle is square root of 1/6, not 6, times the length of the corresponding side of ABCD.
Choice B is incorrect. This is the area of a rectangle where the length of each side of the rectangle is square root 2/3 , not 6, times the length of the corresponding side of ABCD.
Choice C is incorrect. This is the area of a rectangle where the length of each side of the rectangle is square root 6, not 6, times the length of the corresponding side of ABCD.
Problem Statement:
Rectangles ABCD and EFGH are similar. The side lengths of EFGH are 6 times the side lengths of ABCD. The area of ABCD is given as 54 square units. We are tasked with finding the area of EFGH.
Step-by-Step Solution:
Step 1: Understand the relationship between similar rectangles
When two rectangles are similar:
~ Their corresponding side lengths have the same ratio (scaling factor).
~ The ratio of their areas is the square of the ratio of their corresponding side lengths.
Here, the side lengths of EFGH are 6 times the side lengths of ABCD. Thus, the scaling factor for the side lengths is:
k = 6.
The ratio of the areas of the two rectangles is:
Area Ratio = k2 = 62 = 36.
Step 2: Use the area ratio to find the area of EFGH
The area of ABCD is given as 54 square units. Since the area of EFGH is 36 times the area of ABCD, we calculate:
Area of EFGH = 36 ⋅ Area of ABCD = 36 ⋅ 54.
Perform the multiplication:
36 ⋅ 54 = 1,944.
Thus, the area of EFGH is: 1,944 square units.
Verification:
1) The scaling factor for the side lengths is 6, and the scaling factor for the area is 62 = 36.
2) The calculation 36 ⋅ 54 = 1,944 is correct.
Final Answer: D) 1,944.
18th Question
Question:
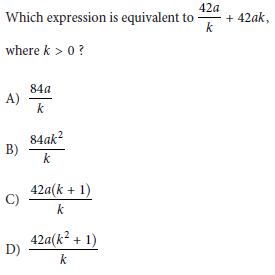
Choice D:

Choice A is incorrect. This expression is equivalent to 42a/k + 42a/k.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect. This expression is equivalent to 42a/k + 42a.
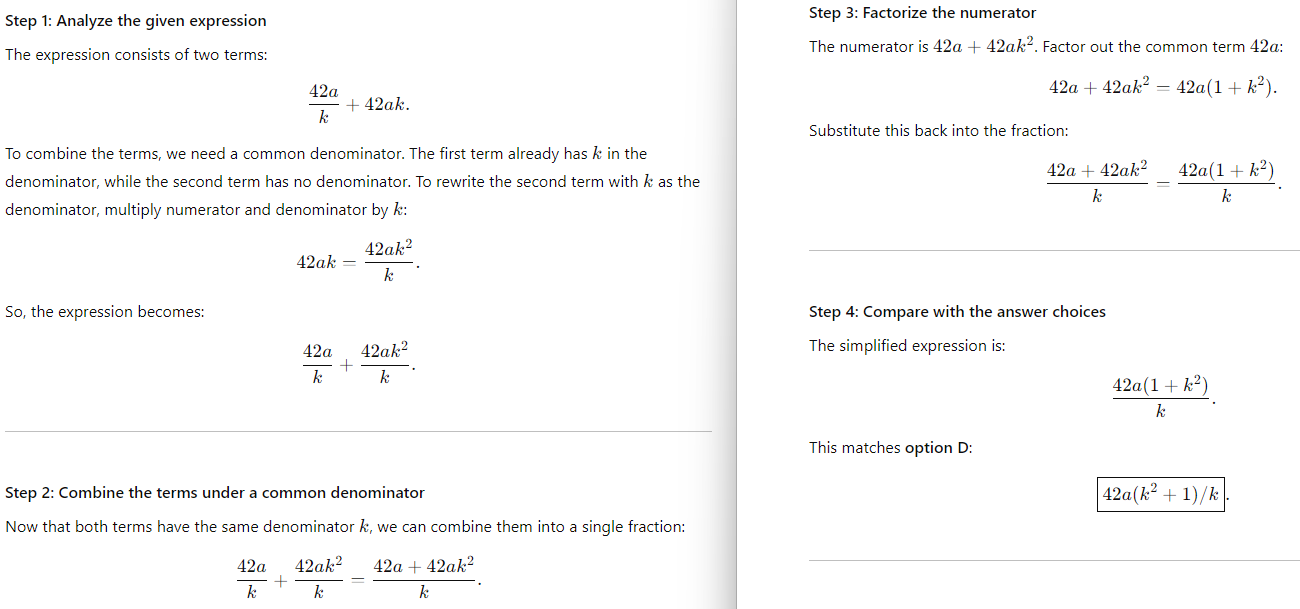
Step-by-Step Solution:
Verification:
1) Expanded numerator 42a(1 + k2) gives 42a + 42ak2, which matches the original expression.
2) Common denominator k was applied correctly.
Final Answer: Option D.
19th Question
Question: Which quadratic equation has no real solutions?
A) x2 + 14x − 49 = 0
B) x2 − 14x + 49 = 0
C) 5x2 − 14x − 49 = 0
D) 5x2 − 14x + 49 = 0
Choice D is correct. The number of solutions to a quadratic equation in the form ax2 + bx + c = 0, where a, b, and c are constants, can be determined by the value of the discriminant, b2 – 4ac. If the value of the discriminant is greater than zero, then the quadratic equation has two distinct real solutions. If the value of the discriminant is equal to zero, then the quadratic equation has exactly one real solution. If the value of the discriminant is less than zero, then the quadratic equation has no real solutions. For the quadratic equation in choice D, 5x2 – 14x + 49 = 0, a = 5, b = -14, and c = 49. Substituting 5 for a, -14 for b, and 49 for c in b2 – 4ac yields (-14)2 – 4(5)(49), or -784. Since -784 is less than zero, it follows that the quadratic equation 5x2 – 14x + 49 = 0 has no real
solutions.
Choice A is incorrect. The value of the discriminant for this quadratic equation is 392. Since 392 is greater than zero, it follows that this quadratic equation has two real solutions.
Choice B is incorrect. The value of the discriminant for this quadratic equation is 0. Since zero is equal to zero, it follows that this quadratic equation has exactly one real solution.
Choice C is incorrect. The value of the discriminant for this quadratic equation is 1,176. Since 1,176 is greater than zero, it follows that this quadratic equation has two real solutions.
Problem Statement:
We are tasked to identify which quadratic equation among the given options has no real solutions. To determine this, we need to use the discriminant of a quadratic equation.
Step-by-Step Solution:
Step 1: Recall the quadratic equation and discriminant formula
The general quadratic equation is:
ax2 + bx + c = 0,
where:
~ a is the coefficient of x2,
~ b is the coefficient of x,
~ c is the constant.
The discriminant (Δ) of a quadratic equation is:
Δ = b2 − 4ac.
~ If Δ > 0, the equation has two real solutions.
~ If Δ = 0, the equation has one real solution.
~ If Δ < 0, the equation has no real solutions (solutions are complex).
Step 2: Analyze each equation
Option A: x2 + 14x − 49 = 0
Here: a = 1, b = 14, c = −49.
Compute the discriminant:
Δ = b2 − 4ac
Δ = (14)2 − 4(1)(−49)
Δ = 196 + 196
Δ = 392.
Since Δ = 392 > 0, this equation has two real solutions.
Option B: x2 − 14x + 49 = 0
Here: a = 1, b = −14, c = 49.
Compute the discriminant:
Δ = b2 − 4ac
Δ = (−14)2 − 4(1)(49)
Δ = 196 − 196
Δ = 0.
Since Δ = 0, this equation has one real solution.
Option C: 5x2 − 14x − 49 = 0
Here:
a = 5, b = −14, c = −49.
Compute the discriminant:
Δ = b2 − 4ac
Δ = (−14)2 − 4(5)(−49)
Δ = 196 + 980
Δ = 1176.
Since Δ = 1176 > 0, this equation has two real solutions.
Option D: 5x2 − 14x + 49 = 0
Here:
a = 5, b = −14, c = 49.
Compute the discriminant:
Δ = b2 − 4ac
Δ = (−14)2 − 4(5)(49)
Δ = 196 − 980
Δ = −784.
Since Δ = −784 < 0, this equation has no real solutions.
Step 3: Final Answer
The quadratic equation with no real solutions is: D) 5x2 − 14x + 49 = 0.
20th Question
P(t) = 260(1.04)(6/4)t
Question: The function P models the population, in thousands, of a certain city t years after 2003. According to the model, the population is predicted to increase by 4% months n. What is the value of n?
A) 8
B) 12
C) 18
D) 72
Choice A is correct. It’s given that the function P models the population, in thousands, of a certain city t years after 2003. The value of the base of the given exponential function, 1.04, corresponds to an increase of 4% for every increase of 1 in the exponent, (6/4)t. If the exponent is equal to 0, then (6/4)t. Multiplying both sides of this equation by (4/6)t yields t = 0. If the exponent is equal to 1, then
(6/4)t = 1. Multiplying both sides of this equation by (4/6) yields t = 4/6, or t = 2/3. Therefore, the population is predicted to increase by 4% every 2/3 of a year. It’s given that the population is predicted to increase by 4% every n months. Since there are 12 months in a year, 2/3 of a year is equivalent to (2/3)(12), or 8, months. Therefore, the value of n is 8.
Choice B is incorrect. This is the number of months in which the population is predicted to increase by 4% according to the model P(t) = 260(1.04)t, not P(t) = 260(1.04)(6/4)t.
Choice C is incorrect. This is the number of months in which the population is predicted to increase by 4% according to the model P(t) = 260(1.04)(4/6)t, not P(t) = 260(1.04)(6/4)t.
Choice D is incorrect. This is the number of months in which the population is predicted to increase by 4% according to the model P(t) = 260(1.04)(6/4)t, not P(t) = 260(1.04)(6/4)t.
Problem Statement:
We are given the function:
P(t) = 260(1.04)(6/4)t,
which models the population P(t) (in thousands) of a city t years after 2003. The population is predicted to increase by 4% every n months. We need to determine the value of n.
Step-by-Step Solution:
Step 1: Analyze the equation
The base of the exponential function, 1.04, represents a 4% increase per interval. The key is to figure out how long this interval (associated with a 4% increase) is in months.
The exponent (6/4)t determines how often this growth occurs:
~ t is in years.
~ 6/4 = 1.5, which means the function grows 1.5 times per year.
Step 2: Convert growth frequency into months
Since 1 year = 12 months:
~ The time interval for each 1.5 growth cycles = 12/1.5 = 8 months.
Thus, the population grows by 4% every 8 months.
Final Answer: The value of n is: 8 months.
Verification:
Given Information:
~ The population at time t = 0 (2003) is P(0) = 260.
~ The growth function is:
P(t) = 260(1.04)(6/4)t.
~ t is measured in years, and we claim that the population grows by 4% every 8 months, which is 2/3 of a year.
Step 1: Substitute t = 2/3 into the function
Since 8 months is equivalent to 2/3 of a year, substitute t = 2/3 into the formula:
P(2/3) = 260(1.04)6/4 ⋅ 2/3.
Step 2: Simplify the exponent
The exponent simplifies as follows:
6/4 ⋅ 2/3
12/12 = 1.
Thus: P(23) = 260(1.04)1
260 ⋅ 1.04
270.4.
Step 3: Verify if this represents a 4% growth
The original population is 260. A 4% increase in 260 is:
260 ⋅ 1.04 = 270.4.
This matches exactly with P(2/3), confirming that a 4% growth occurs after 8 months.
Final Verification
We’ve shown mathematically that the population grows by 4% after t = 2/3 years, which corresponds to 8 months. Therefore, the answer is correct.
21th Question
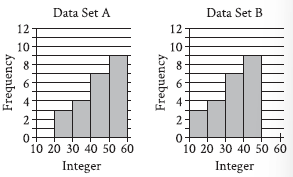
Question: Two data sets of 23 integers each are summarized in the histograms shown. For each of the histograms, the first interval represents the frequency of integers greater than or equal to 10, but less than 20. The second interval represents the frequency of integers greater than or equal to 20, but less than 30, and so on. What is the smallest possible difference between the mean of data set A and the mean of data set B?
A) 0
B) 1
C) 10
D) 23
Choice B is correct. The histograms shown have the same shape, but data set A contains values between 20 and 60 and data set B contains values between 10 and 50. Thus, the mean of data set A is greater than the mean of data set B. Therefore, the smallest possible difference between the mean of data set A and the mean of data set B is the difference between the smallest possible mean of data set A and the greatest possible mean of data set B. In data set A,
since there are 3 integers in the interval greater than or equal to 20 but less than 30, 4 integers greater than or equal to 30 but less than 40, 7 integers greater than or equal to 40 but less than 50, and 9 integers greater than or equal to 50 but less than 60, the smallest possible mean for data set A is (3 • 20) + (4 • 30) + (7 • 40) + (9 • 50)
divided by 23. In data set B, since there are 3 integers greater than
or equal to 10 but less than 20, 4 integers greater than or equal to 20 but less than 30, 7 integers greater than or equal to 30 but less than 40, and 9 integers greater than or equal to 40 but less than 50, the largest possible mean for data set B is (3 • 19) + (4 • 29) + (7 • 39) + (9 • 49) divided by 23. Therefore, the smallest possible difference between the mean of data set A and the mean of data set B is
(3 • 20) + (4 • 30) + (7 • 40) + (9 • 50) divided by 23 subtract from (3 • 19) + (4 • 29) + (7 • 39) + (9 • 49) divided by 23, which is equivalent to
(3 • 20) – (3 • 19) + ( 4 • 30 ) – (4 • 29) + ( 7 • 40 ) – (7 • 39) + ( 9 • 50) – (9 • 49) divided by 23. This expression can be rewritten as 3(20 – 19) + 4(30 – 29) + 7( 40 – 39) + 9(50 – 49), or 23/23, which is equal to 1.
Therefore, the smallest possible difference between the mean of data set A and the mean of data set B is 1.
Choice A is incorrect. This is the smallest possible difference between the ranges, not the means, of the data sets.
Choice C is incorrect. This is the difference between the greatest possible mean, not the smallest possible mean, of data set A and the greatest possible mean of data set B.
Choice D is incorrect. This is the smallest possible difference between the sum of the values in data set A and the sum of the values in data set B, not the smallest possible difference between the means.
Step 1: Analyze the problem
1) What the question asks: We are asked to find the smallest possible difference between the means of two data sets, A and B.
2) Key properties:
~ The histograms for Data Set A and B have the same shape, meaning the number of integers in each interval is identical for both data sets.
~ However, the ranges of the intervals differ:
~ ~ Data Set A: Values range between 20 and 60.
~ ~ Data Set B: Values range between 10 and 50.
3) Key observations:
~ The mean of Data Set A will always be greater than the mean of Data Set B because the values in Data Set A are shifted higher compared to Data Set B.
~ To find the smallest possible difference, we should minimize the mean of Data Set A and maximize the mean of Data Set B.
Step 2: Understand the mean
The mean of a data set is calculated as:
Sum of all values in the data set
Mean = _____________________________________
Number of values in the data set
~ Data Set A and B both contain 23 values.
~ The key is to determine the smallest possible mean of Data Set A and the largest possible mean of Data Set B.
Step 3: Assign values within each interval
Each interval in the histogram represents a range of integers, and we need to assign values to the integers strategically:
1) For Data Set A (minimizing the mean):
Assign the smallest possible value within each interval:
~ For the interval [20, 30): Assign all values to 20.
~ For the interval [30, 40): Assign all values to 30.
~ For the interval [40, 50): Assign all values to 40.
~ For the interval [50, 60): Assign all values to 50.
These assignments minimize the total sum of the data set, leading to the smallest possible mean for Data Set A.
2) For Data Set B (maximizing the mean):
Assign the largest possible value within each interval:
~ For the interval [10, 20): Assign all values to 19.
~ For the interval [20, 30): Assign all values to 29.
~ For the interval [30, 40): Assign all values to 39.
~ For the interval [40, 50): Assign all values to 49.
These assignments maximize the total sum of the data set, leading to the largest possible mean for Data Set B.
Step 4: Calculate the smallest possible mean of Data Set A
Using the histogram for Data Set A:
~ Interval [20, 30): 3 integers, each assigned 20.
~ Interval [30, 40): 4 integers, each assigned 30.
~ Interval [40, 50): 7 integers, each assigned 40.
~ Interval [50, 60): 9 integers, each assigned 50.
The sum of Data Set A is:
= (3 ⋅ 20) + (4 ⋅ 30) + (7 ⋅ 40) + (9 ⋅ 50)
= 60 + 120 + 280 + 450
= 910
The mean of Data Set A is:
MeanA = 910/23 = 39.57 (rounded to two decimal places).
Step 5: Calculate the largest possible mean of Data Set B
Using the histogram for Data Set B:
~ Interval [10, 20): 3 integers, each assigned 19.
~ Interval [20, 30): 4 integers, each assigned 29.
~ Interval [30, 40): 7 integers, each assigned 39.
~ Interval [40, 50): 9 integers, each assigned 49.
The sum of Data Set B is:
= (3 ⋅ 19) + (4 ⋅ 29) + (7 ⋅ 39) + (9 ⋅ 49)
= 57 + 116 + 273 + 441
= 887
The mean of Data Set B is:
MeanB = 887/23 = 38.57 (rounded to two decimal places).
Step 6: Calculate the smallest possible difference between the means
The smallest possible difference is:
Difference = MeanA − MeanB
39.57 − 38.57 = 1.
Step 7: Verify by checking the expression
The calculation can be rewritten as:
Difference= Data Set A − Data Set B
= (3 ⋅ 20) + (4 ⋅ 30) + (7 ⋅ 40) + (9 ⋅ 50) – (3 ⋅ 19) + (4 ⋅ 29) + (7 ⋅ 39) + (9 ⋅ 49)
= (3 ⋅ 20) − (3 ⋅ 19) + (4 ⋅ 30) − (4 ⋅ 29) + (7 ⋅ 40) − (7 ⋅ 39) + (9 ⋅ 50) − (9 ⋅ 49)
= 3(20 − 19) + 4(30 − 29) + 7(40 − 39) + 9(50 − 49)
= 3(1) + 4(1) + 7(1) + 9(1)
= 3 + 4 + 7 + 9
= 23
Divide it by 23 the integers of two Sets A & B:
23/23 = 1.
Final Answer: B) 1.
22th Question
Question:

A) 113
B) 107
C) 101
D) 23
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A:

Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Recall the Pythagorean Theorem
The Pythagorean Theorem states:
a2 + b2 = c2
where a and b are the lengths of the legs of a right triangle, and c is the length of the hypotenuse.
Here:
a = 24, b = 21, c = hypotenuse.
Step 2: Plug values into the theorem
Substitute a = 24 and b = 21:
c2 = 242 + 212
Step 3: Calculate 242 and 212
~ 242 = 576
~ 212 = 441
Now:
c2 =576 + 441
c2 = 1017
Step 4: Find c
To find c, take the square root of both sides:

This matches the original value of c2, confirming that the value of d is correct.
Final Answer: The value of d is: A) 113.
Did you try all the features and get comfortable using them? You should work on using the Desmos calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must attempt as many questions as you can before the final test. This is the 1st Practice Test of SAT Math Module 2nd.
Either you can take the 2nd Practice Test of SAT Math or the 2nd Practice Test of SAT Reading and Writing Module 2nd.
- SAT Test 2nd (Math Module 2nd)
- SAT Test 1st (Math Module 1st)
- SAT Test 2nd (Reading and Writing Module 2nd)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


