
Prepare For The SATs: Math Test Module 1st with Simple Explanations, Tips and Tricks
Did you find the SAT Math complex? If yes, then you are in the right place. We have designed a similar exam format with all the necessary features for you to become a master in Math. You just take the SAT Test Module First to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 1st.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 1ST
The first module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 1st are from easy to difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 1st. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH EQUATION SOLUTIONS WITH EXPLANATION AND TRICKS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
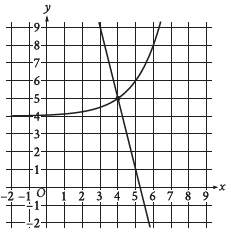
Question: The graph of a system of a linear equation and a nonlinear equation is shown. What is the solution (x, y) to this system?
A) (0,0)
B) (0,4)
C) (4,5)
D) (5,0)
Choice C is correct. The solution to the system of two equations corresponds to the point where the graphs of the equations intersect. The graphs of the linear equation and the nonlinear equation shown intersect at the point (4, 5). Thus, the solution to the system is (4, 5).
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
As you notice in the question, it is written (x, y), so we need to put the value of x first, then y. Whenever you see a crossed line in a graph, focus on the intersected point.
2nd Question
Question: On the first day of a semester, a film club has 90 members. Each day after the first day of the semester, 10 new members join the film club. If no members leave the film club, how many total members will the film club have 4 days after the first day of the semester?
A) 400
B) 130
C) 94
D) 90
Choice B is correct. It’s given that the film club has 90 members on the first day
of a semester, and 10 new members join the film club each day after the first day
of the semester. This means that after 4 days, 4 x 10, or 40, new members will
have joined the club. Adding 40 members to the original 90 club members yields
130 members. Thus, the film club will have 130 total members 4 days after the
first day of the semester.
Choice A is incorrect. This is the number of members that will have joined the film club 4 days after the first day of the semester if 100 new members, not 10, join the film club each day.
Choice C is incorrect. This is the number of members the film club will have 4 days after the first day of the semester if 1 new member, not 10, joins the film club each day.
Choice D is incorrect. This is the number of members the film club has on the first day of the semester.
It is a simple multiply and addition equation, work on your calculation speed by practicing more and more.
Step 1: Understand the Problem
We are asked to find the total number of members in a film club 4 days after the first day of the semester. Here’s what we know:
~ Initial members (on day 1): 90 members.
~ New members per day (starting from day 2): 10 members per day.
~ No members leave the club.
We need to calculate the total number of members 4 days after the first day, meaning we include days 1, 2, 3, 4, and 5.
Step 2: Organize the Information
~ Day 1: Start with 90 members.
~ Day 2: Add 10 new members → 90 + 10 = 100.
~ Day 3: Add 10 new members → 100 + 10 = 110.
~ Day 4: Add 10 new members → 110 + 10 = 120.
~ Day 5 (end of 4th day after the start): Add 10 new members →
120 + 10 = 130.
So, after 4 days, the total number of members in the club is 130.
Step 3: Write a General Formula (You can either use Step 2 or Step 3)
We can generalize this scenario using a formula:
Total Members on Day t = 90 + 10(t−1),
where t is the number of days since the first day.
For t = 5
Total Members = 90 + 10(5 − 1)
= 90 + 10(4)
= 90 + 40 = 130.
Step 4: Answer
The total number of members in the film club 4 days after the first day is: 130
[Step 3 is better when you have given a bigger value than 5 days. The lower the rank of the question, the easier it is in Module 1st, so don’t waste most of your time.]
3rd Question
Question:
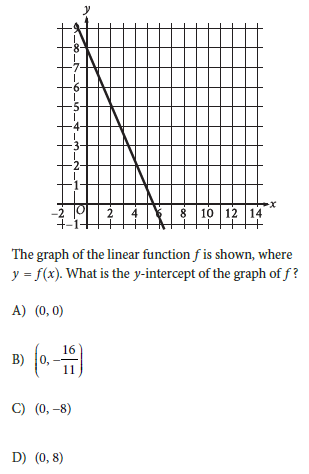
Choice D is correct. The y-intercept of a graph is the point where the graph intersects the y-axis. The graph of a function f shown intersects the y-axis at the point (0, 8). Therefore, the y-intercept of the graph of f is (0, 8).
Choice A is incorrect. This is the point where the x-axis, not the graph of f, intersects the y-axis.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Basically, it just asks for a positive y-axis and the intercepted part.
4th Question
s + 7r = 27
r = 3
Question: What is the solution (r, s) to the given system of equations?
A) (6, 3)
B) (3, 6)
C) (3, 27)
D) (27, 3)
Choice B is correct. The second equation in the given system is r = 3. Substituting 3 for r in the first equation in the given system yields s + 7(3) = 27, or s + 21 = 27. Subtracting 21 from both sides of this equation yields s = 6. Therefore, the solution (r, s) to the given system of equations is (3, 6).
Choice A is incorrect. This is the solution (s, r), not (r, s), to the given system of equations.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
When digits have plus or minus signs then interchanging digits from one side of equal to another side of equal will always change the sign to opposite. Second, we have already given the value of r = 3. So, option A and option D are out of the equation.
Step 1: Understand the Problem
We are solving a system of equations:
~ s + 7r = 27
~ r = 3
We are tasked with finding the solution for the ordered pair (r, s), which represents the values of r and s that satisfy both equations.
Step 2: Substitute the Value of r
From the second equation, r = 3, substitute this value into the first equation s + 7r = 27
s + 7(3) = 27.
Step 3: Simplify the Equation
Simplify the terms: s + 21 = 27.
Step 4: Solve for s
Subtract 21 from both sides to isolate s:
s = 27 − 21.
s = 6.
Step 5: Write the Solution
The solution to the system of equations is: (r, s) = (3, 6).
Step 6: Verify the Solution
Substitute r = 3 and s = 6 into both original equations to ensure they hold true:
1. First equation: s + 7r = 27
6 + 7(3) = 27 ⟹ 6 + 21 = 27. This is true.
2. Second equation: r = 3.
This is already satisfied. Thus, the solution is correct.
Final Answer
The solution is: (3, 6).
5th Question
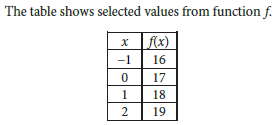
Which of the following is the best description of function f ?
A) Decreasing linear
B) Increasing linear
C) Decreasing exponential
D) Increasing exponential
Choice B is correct. The given values show that as x increases, f (x) also increases, which means that f is an increasing function. Furthermore, f (x) increases at a constant rate of 1 for each increase of x by 1. A function with a constant rate of change is linear. Thus, the function f can be described as an
increasing linear function.
Choice A is incorrect. For a decreasing linear function, as x increases, f (x) decreases rather than increases.
Choice C is incorrect. For a decreasing exponential function, for each increase of x by 1, f (x) decreases by a fixed percentage rather than increases at a constant rate.
Choice D is incorrect. For an increasing exponential function, for each increase of x by 1, f (x) increases by a fixed percentage rather than at a constant rate.
Step 1: Analyze the Question
We are given a table showing selected values of xxx and their corresponding values of f(x). The goal is to identify the type of function f that best describes the relationship between x and f(x).
Step 2: Observe the Table
The table is as follows:
x: −1, 0, 1, 2
f(x): 16, 17, 18, 19
Step 3: Look for a Pattern
~ Rate of Change: Check the difference between consecutive f(x) values:
f(x) = Based on the table – if the value of the x is -1 then the value of the f(x) is 16. If the value of the x is 2 then the value of the f(x) is 19.
Hence, f(x) = f(-1) = 16, we want to know the rate of change then let’s subtract one f(x) value from the latter.
17 – 16 = 1
18 – 17 = 1
19 – 18 = 1
The difference between consecutive f(x) values is constant at 1.
Step 4: Determine the Type of Function
A constant rate of change in f(x) indicates that f is a linear function. This is because linear functions have a constant slope (rate of change).
Step 5: Write the Linear Function
In order to get the value of m, we need the rate of change value of both f(x) and x. Based on the table, we can see, the difference is 1.

Now, we have the value of b. Remember, it is not compulsory to use the value of x = 0 and 17 of f(x) = f(0). You can use any f(x) and x from the table, but it must be from the same row.
For example, x = 2, f(2) = 19.
f(x) = mx + b
19 = 1(2) + b
19 = 2 + b
19 – 2 = b
b = 17. It will always be the same.
Step 6: Verify the Function
Substitute the given x-values into f(x) = x + 17: [m is 1, it doesn’t change anything in the whole equation, so let’s skip it or you can use the complete formula, choice is yours.]
~ For x = −1: f(x) = mx + b OR x + b
f(−1) = −1 + 17 = 16.
~ For x = 0: f(x) = mx + b OR x + b
f(0) = 0 + 17 = 17.
~ For x = 1: f(x) = mx + b OR x + b
f(1) = 1 + 17 = 18.
~ For x = 2: f(x) = mx + b OR x + b
f(2) = 2 + 17 = 19.
The function matches the table.
Step 7: Final Answer
The best description of function f is that it is a (increasing) linear function.
6th Question
Question: A customer spent $27 to purchase oranges at $3 per pound. How many pounds of oranges did the customer purchase?
A) $30
B) $9
C) $24
D) $81
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B: The correct answer is 9. It’s given that the customer spent $27 to purchase oranges at $3 per pound. Therefore, the number of pounds of oranges the customer purchased is $27 (1 pound / $3), or 9 pounds.
Choice A is incorrect because we do not add values here.
Choice C is incorrect because we do not subtract values here.
Choice D is incorrect because we do not multiply values here.
The key points, you need to follow are: we have an overall cost of $27, we have a per pound cost which is $3 and it is asking how many pounds. This informs us to divide.
Step 1: Understand the Question
We are tasked with finding the number of pounds of oranges a customer purchased, given:
~ The total cost spent: $27
~ The price per pound of oranges: $3 per pound
Step 2: Set Up the Problem
Let p represent the number of pounds of oranges purchased. The relationship between the total cost, price per pound, and the number of pounds is expressed as:
Total cost = Price per pound × Number of pounds.
Substituting the given values: 27 = 3p.
Step 3: Solve for p
To find p, divide both sides of the equation by 3:
p = 27/3.
Simplify: p = 9.
Step 4: Verify the Solution
If the customer purchased 9 pounds of oranges at $3 per pound, the total cost would be: 3 × 9 = 27 dollars.
This matches the given total cost, so the solution is correct.
Step 5: Final Answer
The customer purchased 9 pounds of oranges.
7th Question
Question: Nasir bought 9 storage bins that were each the same price. He used a coupon for $63 off the entire purchase. The cost for the entire purchase after using the coupon was $27 . What was the original price, in dollars, for 1 storage bin?
A) $90
B) $10
C) $35
D) $81
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B: The correct answer is 10. It’s given that the cost for the entire purchase was $27 after a coupon was used for $63 off the entire purchase. Adding the amount of the coupon to the purchase price yields 27+63=90. Thus, the cost for the entire purchase before using the coupon was $90. It’s given that Nasir bought 9 storage bins. The original price for 1 storage bin can be found by dividing the total cost by 9. Therefore, the original price, in dollars, for 1 storage bin is 90/9, or 10.
Choice A is incorrect because we do not add values here.
Choice C is incorrect because we do not subtract values here.
Choice D is incorrect because we do not add and subtract values here.
Asking for one storage price and buying 9 bins, he paid $27 but he used a coupon with a $63 discount for calculation, we need the original price, as it is stated at the end of the question. So, $27 + $63 and then divide them the same way we did question 6th.
Step 1: Understand the Question
We are tasked with finding the original price of 1 storage bin. Here’s what we know:
~ Nasir bought 9 storage bins, all at the same price.
~ He used a coupon that took $63 off the total purchase price.
~ After applying the coupon, the total cost of the bins was $27.
We need to find the original price of 1 storage bin.
Step 2: Set Up the Problem
Let the original price of 1 storage bin be p dollars. The total cost before applying the coupon is:
Total original cost = 9p.
After applying the coupon, the equation for the final total cost becomes:
9p − 63 = 27.
Step 3: Solve the Equation
Start with the equation: 9p − 63 = 27.
Step 3.1: Add 63 to both sides
9p = 27 + 63.
9p = 90.
Step 3.2: Divide by 9 to isolate p
p = 90/9.
p = 10.
Step 4: Verify the Solution
If the original price of 1 bin is $10:
~ The total cost for 9 bins is: 9 × 10 = 90 dollars.
~ After applying the $63 coupon, the total becomes: 90 − 63 = 27 dollars.
This matches the given final cost, so the solution is correct.
Step 5: Final Answer
The original price for 1 storage bin was $10.
8th Question
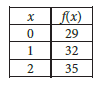
Question: For the linear function f, the table shows three values of x and their corresponding values of f(x). Which equation defines f(x)?
A) f(x) = 3x + 29
B) f(x) = 29x + 32
C) f(x) = 35x + 29
D) f(x) = 32x + 35
Choice A is correct. An equation that defines a linear function f can be written in the form f(x) = mx + b, where m and b are constants. It’s given in the table that when x = 0, f(x) = 29. Substituting 0 for x and 29 for f(x) in equation f(x) = mx + b yields 29 = m(0) + b, or 29 = b. Substituting 29 for b in the
equation f(x) = mx + b yields f(x) = mx + 29. It’s also given in the table that when x = 1, f(x) = 32. Substituting 1 for x and 32 for f(x) in the equation f(x) = mx + 29 yields 32 = m(1) + 29, or 32 = m + 29. Subtracting 29 from both sides of this equation yields 3 = m. Substituting 3 for m in the equation
f(x) = mx + 29 yields f(x) = 3x + 29.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
It simply asks you to calculate the difference between each f(x). The answer is 32 – 29 = 3. The most important thing that helps you find the right option is the value of the difference. You can also use 32 or 35 instead of 29 if there are such options or a Type-Based Question.
Step 1: Understand the Question

[It is somewhat similar to Question 5; you use the same formula to find the value of m.]
Step 3: Find the y-intercept (b)
Using the slope-intercept form f(x) = mx + b, substitute a point from the table to solve for b.
Using x = 0 and f(x) = 29:
f(x) = mx + b.
29 = 3(0) + b.
b = 29.
Thus, the y-intercept is b = 29.
Step 4: Write the Equation
The equation for f(x) is: f(x) = 3x + 29.
Step 5: Verify the Equation
Check the equation f(x) = 3x + 29 with the given values in the table:
1. For x = 0:
f(0) = 3(0) + 29 = 29. (Correct!)
2. For x = 1:
f(1) = 3(1) + 29 = 32. (Correct!)
3. For x = 2:
f(2) = 3(2) + 29 = 35. (Correct!)
Thus, the equation is verified.
Final Answer
The linear function equation is: f(x) = 3x + 29.
9th Question
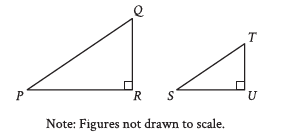
Question: Right triangles PQR and STU are similar, where upper P corresponds to S. If the measure of angle Q is 18°, what is the measure of angle S ?
A) 18°
B) 72°
C) 82°
D) 162°
Choice B is correct. In similar triangles, corresponding angles are congruent. It’s given that right triangles PQR and STU are similar, where angle P corresponds to angle S. It follows that angle P is congruent to angle S. In the triangles shown, angle R and angle U are both marked as right angles, so angle R and angle U are corresponding angles. It follows that angle Q and angle T are corresponding
angles, and thus, angle Q is congruent to angle T . It’s given that the measure of angle Q is 18 degrees, so the measure of angle T is also 18 degrees. Angle U is a right angle, so the measure of angle U is 90 degrees. The sum of the measures of the interior angles of a triangle is 180 degrees. Thus, the sum of the measures of the interior angles of triangle STU is 180 degrees. Let’s represent the measure, in degrees, of the angle S. It follows that s + 18 + 90 = 180, or s + 108 = 180. Subtracting 108 from both
sides of this equation yields s = 72. Therefore, if the measure of angle Q is 18 degrees, then the measure of angle S is 72 degrees.
Choice A is incorrect. This is the measure of angle T.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect. This is the sum of the measures of angle S and angle U.
Always remember, the straight verticle line is 90 degrees and the straight horizontal line is 180 degrees. So, STU = 180 degrees. As the question suggested both both triangles are the same. Q = T. Now, put the value s + 18 + 90 = 180.
Step 1: Understand the Problem
We are given two similar right triangles, △PQR and △STU, where the corresponding vertices are P → S, Q → T, and R → U. Additionally:
~ ∠Q = 18∘.
~ The problem asks us to find the measure of ∠S.
Step 2: Properties of Similar Triangles
For similar triangles:
1. Corresponding angles are equal.
2. The sum of the angles in any triangle is 180∘.
Since the triangles are right triangles: ∠R = ∠U = 90∘.
Thus: ∠Q corresponds to ∠T.
Therefore: ∠T = ∠Q = 18∘.
Step 3: Calculate ∠S
In triangle △STU, the angles must add up to 180∘:
∠S + ∠T + ∠U = 180∘.
Substitute the known values: ∠S + 18∘ + 90∘ = 180∘.
Simplify: ∠S + 108∘ = 180∘.
Solve for ∠S: ∠S = 180∘ − 108∘ = 72∘.
Final Answer
The measure of ∠S is: 72∘.
10th Question
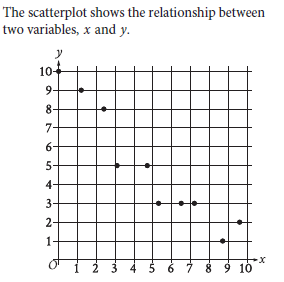
Question: Which of the following equations is the most appropriate linear model for the data shown?
A) y = 0.9 + 9.4x
B) y = 0.9 − 9.4x
C) y = 9.4 + 0.9x
D) y = 9.4 − 0.9x
Choice D is correct. The data points suggest that as the variable x increases, the variable y decreases, which implies that an appropriate linear model for the data has a negative slope. The data points also show that when x is close to 0, y is greater than 9. Therefore, the y-intercept of the graph of an appropriate linear model has a y-coordinate greater than 9. The graph of an equation of the form
y = a + bx, where a and b are constants, has a y-intercept with a y-coordinate of a and has a slope of b. Of the given choices, only choice D represents a graph that has a negative slope, -0.9, and a y-intercept with a y-coordinate greater than 9, 9.4.
Choice A is incorrect. The graph of this equation has a positive slope, not a negative slope, and a y-intercept with a y-coordinate less than 1, not greater than 9.
Choice B is incorrect. The graph of this equation has a y-intercept with a y-coordinate less than 1, not greater than 9.
Choice C is incorrect. The graph of this equation has a positive slope, not a negative slope.
You don’t need to find the exact measure, they easily describe it for you. Notice all the options, you will find the same digits but the position and signs are different. They asked for the relation between two variables, so we need to find something that has somewhat connection. If you notice, you will find “9y, 1x” has an intercept and similarly “1y, 9x” has one too.
Step-by-Step Detailed Solution:
Step 1: Understand the Problem
We are tasked with identifying the correct linear equation that models the data points in the scatterplot. Linear equations take the form:
y = mx + b
where:
~ m is the slope (the rate at which y changes as x changes),
~ b is the y-intercept (the value of y when x = 0).

Thus, the slope is approximately −0.9.
Step 4: Write the Linear Equation
The equation of the line is: y = mx + b
Substituting the estimated values of m = −0.9 and b = 9.4, we get:
y = 9.4 − 0.9x
Step 5: Compare with Given Options
Now compare the derived equation with the provided options:
1. Option A: y = 0.9 + 9.4x
~ m = 9.4 (positive slope), which contradicts the scatterplot’s negative trend.
~ Eliminate Option A.
2. Option B: y = 0.9 − 9.4x
~ m = −9.4, which is negative (correct), but b = 0.9 does not match the y-intercept of approximately 9.4.
~ Eliminate Option B.
3. Option C: y = 9.4 + 0.9x
~ m = 0.9 (positive slope), which contradicts the scatterplot’s negative trend.
~ Eliminate Option C.
4. Option D: y = 9.4 − 0.9x
~ m = −0.9 (negative slope) matches the observed trend.
~ b = 9.4 matches the observed y-intercept.
Option D is correct.
Final Answer:
D) y = 9.4 − 0.9x
Step 6: Verify the Solution
Using the derived equation y = 9.4 − 0.9x, plug in values of x to check consistency:
~ For x = 4: y = 9.4 − 0.9x
y = 9.4 − 0.9(4)
y = 9.4 − 3.6
y = 5
This matches the point (4, 5) from the scatterplot.
~ For x = 10: y = 9.4 − 0.9x
y = 9.4 − 0.9(10)
y = 9.4 − 9
y = 0
This matches the point (10, 0) from the scatterplot.
The derived equation is consistent with the data.
11th Question
Question:
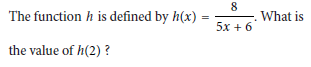
A) 2
B) 1
C) 0.25 or 1/4
D) 0.5 or 1/2
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D:

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
The question again gives us a hint. The value of h(x) is h(2), which means we know x is 2. Now, solve the equation.
Step-by-Step Solution:
Step 1: Understand the Problem
The function h(x) is given in terms of x. To find h(2), substitute x = 2 into the function and compute the result.
The function is written as:

Final Answer:
Thus, h(2) = 1/2 or 0.5.
12th Question
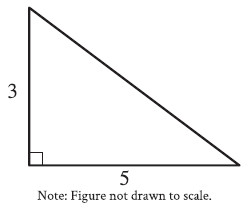
Question: The figure shows the lengths, in inches, of two sides
of a right triangle. What is the area of the triangle, in
square inches?
A) 15/2 or 7.5
B) 8/2 or 4
C) 15
D) 8
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A:

Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
In simple words, if you see a question like this, remember one thing the sloppy angle is half of the multiplication of horizontal and vertical vertex (line). Look 5 x 3 = 15, now half of it is 7.5 or 15/2.
Problem:
We are tasked to calculate the area of a right triangle. The given triangle has:
~ A base of 5 inches
~ A height of 3 inches

Final Answer:
The area of the triangle is: 7.5 square inches
13th Question
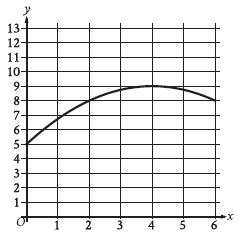
Question: The graph models the number of active projects a
company was working on x months after the end of
November 2012, where 0 ≤ x ≤ 6. According to the
model, what is the predicted number of active
projects the company was working on at the end of
November 2012?
A) 0
B) 5
C) 8
D) 9
Choice B is correct. It’s given that the graph models the number of active projects a company was working on x months after the end of November 2012. Therefore, the value of x that corresponds to the end of November 2012 is 0. The point at which x = 0 is the y-intercept of the graph. It follows that the y-intercept of the graph shown is the point (0, 5). Therefore, according to the model, the predicted
number of active projects the company was working on at the end of November 2012 is 5.
Choice A is incorrect. This is the value of x that corresponds to the end of November 2012, not the predicted number of active projects the company was working on at the end of November 2012.
Choice C is incorrect. This is the predicted number of active projects the company was working on 2 months after the end of November 2012.
Choice D is incorrect. This is the predicted number of active projects the company was working on 4 months after the end of November 2012.
Don’t beat yourself up! This sign means (≤) less or equal than which means 0 ≤ x ≤ 6. We need to find the x value, according to the sign, we need a digit that is less than or equal to 6 but 0 is also less than x. So, the options make it easy for you, 5 is that value. Take a look at the options.
Step 1: Locate x = 0 on the graph
~ The horizontal axis (x) represents the time in months after November 2012.
~ At x = 0, we need to read the value of y, which represents the number of active projects.
Step 2: Carefully observe the graph
Looking at the graph:
1. At x = 0, the point on the graph appears to intersect the y-axis at y = 5.
2. This indicates that the company was predicted to have 5 active projects at the end of November 2012.
Final Answer:
The predicted number of active projects the company was working on at the end of November 2012 is: B) 5
14th Question
Question:
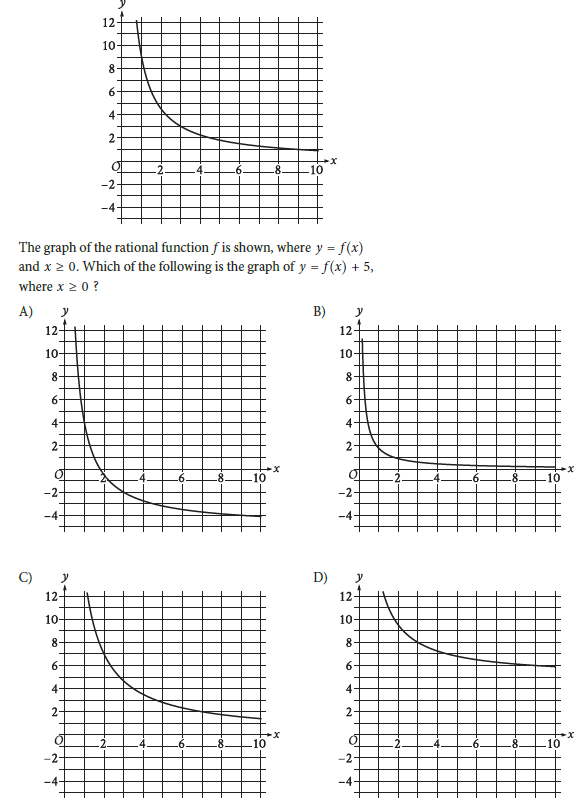
Choice D is correct. It’s given that the graph of the rational function f is shown, where y = f(x) and x ≥ 0. The graph shown passes through the point (3, 3). It follows that when the value of x is 3, the value of f(x) is 3. When the value of f(x) is 3, the value of f(x) + 5 is 3 + 5, or 8. Therefore, the graph of y = f(x) + 5 passes through the point (3, 8). Of the given choices, choice D is the only graph that passes through the point (3, 8) and is, therefore, the graph of y = f(x) + 5.
Choice A is incorrect. This is the graph of y = f(x) – 5, rather than y = f(x) + 5.
Choice B is incorrect. This is the graph of y = f(x)/5, rather than y = f(x) + 5.
Choice C is incorrect and may result from conceptual or calculation errors.
In simple words, it says (x ≥ 0), x is bigger or equal to 0 then the value of y = f(x) + 5. If we add 5 to the f(x), it should become y. So according to the graph from the value of x, you will see a gap of 1. If we pick 3 and add 5 to it, it will become 8. Check-in option D (between 2 and 4 of the x-axis and 8 of the y-axis), and you will notice an intercept. [But if we use something else except 3, it won’t intercept.]
Step 1: Understand the Transformation
Adding a constant +5 to the function f(x) creates a vertical shift in the graph. Specifically:
~ For any point (x, y) on the graph of y = f(x), the corresponding point on y = f(x) + 5 is (x, y + 5).
~ This means every point on the graph of y = f(x) will be shifted up by 5 units.
Step 2: Analyze Key Points on the Original Graph
From the given graph of y = f(x), let’s identify a key point to track the vertical shift:
~ One clear point on the original graph is (3, 3) (as the curve intersects y = 3 when x = 3).
For y = f(x) + 5, the corresponding new point will be:
y = 3 + 5 = 8.
Thus, the new graph must pass through the point (3, 8).
Step 3: Examine the Options
Now, look at the provided graphs:
~ Option A: The graph passes through (3, 3), which is the original graph of y = f(x).
~ Option B: The graph appears shifted, but it does not pass through (3, 8).
~ Option C: The graph appears to be shifted down rather than up, which does not match y = f(x) + 5.
~ Option D: This graph has been shifted up by 5 units and passes through (3, 8).
Thus, Option D is correct.
Step 4: Verify Option D
~ The original graph has a horizontal asymptote at y = 0.
~ Adding 5 to f(x) shifts the asymptote to y = 5, as shown in Option D.
~ This matches the expected behavior of y = f(x) + 5
15th Question
Question: At a particular track meet, the ratio of coaches to athletes is 1 to 26. If there are x coaches at the track meet, which of the following expressions represents the number of athletes at the track meet?
A) x/26
B) 26x
C) x + 26
D) 26/x
Choice B is correct. It’s given that at a particular track meet, the ratio of coaches to athletes is 1 to 26. If one number in a ratio is multiplied by a value, the other number must be multiplied by the same value in order to maintain the same ratio. If there are x coaches at the track meet, multiplying both numbers in the ratio by x yields 1(x) to 26(x), or x to 26x. Therefore, the expression 26x represents the
number of athletes at the track meet.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
To find out any value from a ratio, we must multiply both sides with the same value, the value is unknown and mentioned as x. According to the question, coached to athletes (1 to 26), so 1 coach for 26 athletes. If there are x coaches then how many athletes? 1x : 26x = x : 26x, the question only ask for athletes = 26x.
Problem Analysis:
We are tasked to find an expression that represents the number of athletes at a track meet given that the ratio of coaches to athletes is 1 : 26, and there are x coaches. The solution requires setting up and solving a proportional relationship.
Step-by-Step Solution:
Step 1: Understand the ratio
The ratio 1 : 26 means:
~ For every 1 coach, there are 26 athletes.
Step 2: Represent the relationship algebraically
If there are x coaches, the ratio of coaches to athletes is still maintained at 1 : 26. Therefore, the number of athletes can be calculated as:
Number of athletes = 26 ⋅ x
This is because for every coach, there are 26 athletes, and if there are x coaches, the number of athletes is proportional to x.
Step 3: Verify the proportionality
To confirm:
~ When x = 1 (1 coach), the number of athletes is 26 × 1 = 26, consistent with the given ratio.
~ When x = 2 (2 coaches), the number of athletes is 26 × 2 = 52, maintaining the 1 : 26 ratio. Thus, the relationship 26x correctly represents the number of athletes.
Final Expression:
The number of athletes at the track meet is given by: 26x
16th Question
y ≤ x + 7
y ≥ −2x −1
Question: Which point (x, y) is a solution to the given system of inequalities in the xy-plane?
A) (−14, 0)
B) (0, −14)
C) (0, 14)
D) (14, 0)
Choice D is correct. A point (x, y) is a solution to a system of inequalities in the xy-plane if substituting the x-coordinate and the y-coordinate of the point for x and y, respectively, in each inequality makes both of the inequalities true. Substituting the x-coordinate and the y-coordinate of choice D, 14 and 0, for x and y, respectively, in the first inequality in the given system, y ≤ x + 7, yields 0 ≤ 14 + 7, or 0 ≤ 21, which is true. Substituting 14 for x and 0 for y in the second inequality in the given system, y ≥ -2x – 1, yields 0 ≥ -2(14) -1, or 0 ≥ -29, which is true. Therefore, the point (14, 0) is a solution to the given system of inequalities in the xy-plane.
Choice A is incorrect. Substituting -14 for x and 0 for y in the inequality y ≤ x + 7 yields 0 ≤ -14 + 7, or 0 ≤ -7, which is not true.
Choice B is incorrect. Substituting 0 for x and -14 for y in the inequality y ≥ -2x – 1, yields -14 ≥ -2(0) -1, or -14 ≥ -1, which is not true.
Choice C is incorrect. Substituting 0 for x and 14 for y in the inequality y ≤ x + 7 yields 14 ≤ 0 + 7, or 14 ≤ 7, which is not true.
Develop fast analytical skills by practicing more. Here the key is to be able to understand the chart quickly.
Problem Statement:
We are solving a system of linear inequalities:
~ y ≤ x + 7
~ y ≥ −2x −1
The task is to identify which of the given points satisfies both inequalities. The solution will be determined by substituting each point into both inequalities.
Step-by-Step Solution:
Step 1: Analyze the inequalities
1. First inequality: y ≤ x + 7
~ The line y = x + 7 has a slope of 1 and a y-intercept of 7.
~ y ≤ x + 7 means the region is below or on the line y = x + 7.
2. Second inequality: y ≥ −2x −1y
~ The line y = −2x −1 has a slope of −2 and a y-intercept of −1.
~ y ≥ −2x −1 means the region is above or on the line y = −2x −1.
The solution to the system is the region of overlap between these two inequalities.
Step 2: Test each given point
We will substitute each point (x, y) into both inequalities and check whether they are satisfied.
Option A: (−14, 0)
1. Substitute into y ≤ x + 7:
0 ≤ −14 + 7 ⟹ 0 ≤ −7 (False)
Since this point does not satisfy the first inequality, it is not a solution.
Option B: (0,−14)
1. Substitute into y ≤ x + 7:
−14 ≤ 0 + 7 ⟹ −14 ≤ 7 (True)
2. Substitute into y ≥ −2x −1:
−14 ≥ −2(0) −1 ⟹ −14 ≥ −1 (False)
Since this point does not satisfy the second inequality, it is not a solution.
Option C: (0,14)
1. Substitute into y ≤ x + 7:
14 ≤ 0 + 7 ⟹ 14 ≤ 7 (False)
Since this point does not satisfy the first inequality, it is not a solution.
Option D: (14,0)
1. Substitute into y ≤ x + 7:
0 ≤ 14 + 7 ⟹ 0 ≤ 21 (True)
2. Substitute into y ≥ −2x−1:
0 ≥ −2(14) −1 ⟹ 0 ≥ −28 −1 ⟹ 0 ≥ −29 (True)
Since this point satisfies both inequalities, it is a solution.
Let’s break it down in detail:
Step 1: Substitute (14,0) into the First Inequality (y ≤ x + 7)
The inequality is: y ≤ x + 7
Substitute x = 14 and y = 0 into the inequality:
0 ≤ 14 + 7
Simplify: 0 ≤ 21
This inequality is true because 0 is indeed less than or equal to 21.
Step 2: Substitute (14,0) into the Second Inequality (y ≥ −2x −1)
The inequality is: y ≥ −2x − 1
Substitute x = 14 and y = 0 into the inequality:
0 ≥ −2(14) −1
Simplify:
0 ≥ −28 −1
0 ≥ −29
This inequality is true because 0 is greater than −29.
Conclusion:
(14, 0) satisfies both inequalities, so it is the solution.
17th Question
Question:
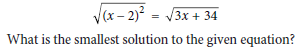
A) 10
B) 7
C) -3
D) 13
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice C:
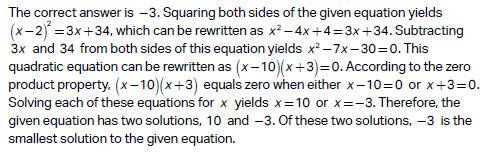
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
A simple yet strange method in math that you can use by doing addition, subtraction, multiplication, and division of any number into the given equation. For example, here, we remove the root from both sides. The second thing is when we change sides the minus or plus sign changes to its opposite also. For example, 3x + 34 goes to the left side and becomes -3x – 34.
Step 1: Understand the Square Root of a Square
The square root of (x−2)2 is |x – 2|, which accounts for both the positive and negative roots:

We will now solve each case separately.

Thus, the solutions are:
x = 10 or x = −3.
Check the Condition (x − 2 ≥ 0)
For this case, x − 2 ≥ 0 ⟹ x ≥ 2.
~ x = 10 satisfies this condition.
~ x = −3 does not satisfy this condition.
So, the valid solution for Case 1 is:
x = 10.

Thus, the solutions are:
x = 10 or x = −3.
Check the Condition (x − 2 < 0)
For this case, x − 2 < 0 ⟹ x < 2.
~ x = 10 does not satisfy this condition.
~ x = −3 satisfies this condition.
So, the valid solution for Case 2 is:
x = −3.
Step 5: Find the Smallest Solution
The two solutions are:
x = 10 and x = −3.
The smallest solution is: -3.
18th Question
Question: The expression 4x2 + bx − 45, where b is a constant, can be rewritten as (hx + k)(x + j), where h, k, and j are integer constants. Which of the following must be an integer?
A) b/h
B) b/k
C) 45/h
D) 45/k
Choice D

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
(hx + k) (x + j), you can multiply every value to one another like ‘hx to x,’ ‘hx to j,’ ‘k to x,’ and ‘k to j.’ Did you notice ‘kj’ which is my name? Using it might get you more marks. There is another one but use this one, it is easy. The second way is to take a common value out of it ‘hx2 + hxj + kx + kj.’ If you notice the x in the middle values is common, so put it out and put ‘hj + k’ inside the bracket. You will surely get more marks, not cause of using my name, but because it is the 18th question. The higher the question rank, the more marks you will get.
Problem Restatement:
The quadratic expression 4x2 + bx − 45 can be factored into the form (hx + k)(x + j), where h, k, and j are integers. We need to identify which expression must be an integer.

Step 4: Identify which expression must be an integer
In the factorization, j =−45/k must be an integer for the equation to hold. Since j depends on k, and j = −45/k, the numerator −45 must be divisible by k.
Therefore, the expression: 45/k
is guaranteed to be an integer because k is constrained to be a factor of 45. This ensures that j is an integer, satisfying the factorization requirement.
[One more easy way to understand, why the -45 change into 45.
k . j = -45
That is what we have. When we change the direction of one number or letter from one side to another side then we change its sign, so if it is positive, it will become negative.
Hence;
j = -45 / -k
We cut the negative sign to the negative sign and we will get:
j = 45/k]
19th Question
y = 2x2 − 21x + 64
y = 3x + a
Question: In the given system of equations, ‘a‘ is a constant. The graphs of the equations in the given system intersect at exactly one point, (x, y), in the xy-plane. What is the value of x?
A) −8
B) −6
C) 6
D) 8
Choice C:

Choice A is incorrect. This is the value of a, not x.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
If you thinking of using the formula of (a2 – 2ab + b2), you cannot. The first reason is 2x2, for it to be a2 both values should have a square, but here 2 does not have a square. The second is you cannot get 21x if you calculate it as 2ab.
Problem Breakdown:
We are tasked with finding the value of x where the two equations:
~ y = 2x2 − 21x + 64
~ y = 3x + a
intersect at exactly one point. This requires solving the system of equations by setting the two expressions for y equal to each other. Since the two curves intersect at exactly one point, the quadratic equation that results must have exactly one solution, implying the discriminant of the quadratic equation equals zero.
Step-by-Step Solution:
1. Set the two equations equal to each other:
2x2 − 21x + 64 = 3x + a
2. Rearrange into standard quadratic form:
Move all terms to one side: 2x2 −21x − 3x + 64 − a = 0
Simplify: 2x2 − 24x + (64 − a) = 0
This is our quadratic equation: 2x2 − 24x + (64 − a) = 0
3. Apply the condition for exactly one intersection:
A quadratic equation has exactly one solution when its discriminant (Δ) is equal to 0. The discriminant for a quadratic equation ax2 + bx + c = 0 is given by: Δ = b2 − 4ac
Here:
~ a = 2
~ b = −24
~ c = 64 − a
Substitute these into the discriminant formula:
Δ = (−24)2 − 4(2)(64 − a)
Simplify: Δ = 576 − 8(64−a)
Δ = 576 − 512 + 8a
Δ = 64 + 8a
4. Set the discriminant equal to 0:
64 + 8a = 0
Solve for a:
8a = −64
a = −8
5. Solve for x:
Now that a = −8, substitute y = 3x − 8 into y = 2x2 − 21x + 64 and solve for x:
2x2 − 21x + 64 = 3x − 8
Simplify: 2x2 − 24x + 72 = 0
Factorize: 2(x2 − 12x + 36) = 0
x2 − 12x + 36 = 0 [Here, a = x, b = 6, a2 = x2, b2 = 62 (36), and 2ab = 2.x.6 (12). It is a factor. a2 – 2ab + b2]
(x − 6)2 = 0 [We use a formula here: (a – b)2 = a2 – 2ab + b2 ]
So: x = 6
How and why do we get 6 as an answer?
Mathematically, when solving a quadratic equation like (x − 6)2 = 0 = 0, the factored form already shows repeated roots (a double root). In this case, x − 6 appears twice: (x − 6)(x − 6) = 0
Thus, the quadratic equation has only one unique solution, x = 6, because the same root is counted twice.
20th Question
Question: An isosceles right triangle has a hypotenuse of length 58 inches. What is the perimeter, in inches, of this triangle?
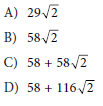
Choice C:

Choice A is incorrect. This is the length, in inches, of each of the congruent sides of the triangle, not the perimeter, in inches, of the triangle.
Choice B is incorrect. This is the sum of the lengths, in inches, of the congruent sides of the triangle, not the perimeter, in inches, of the triangle.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown
We are dealing with an isosceles right triangle, where:
~ The hypotenuse is 58 inches.
~ The two legs are of equal length (a).
~ The perimeter needs to be found.
We are to match the perimeter with the given options:

Step 3: Calculate the perimeter
The perimeter of a triangle is the sum of all its sides:
Perimeter = leg + leg + hypotenuse
Substitute the values:
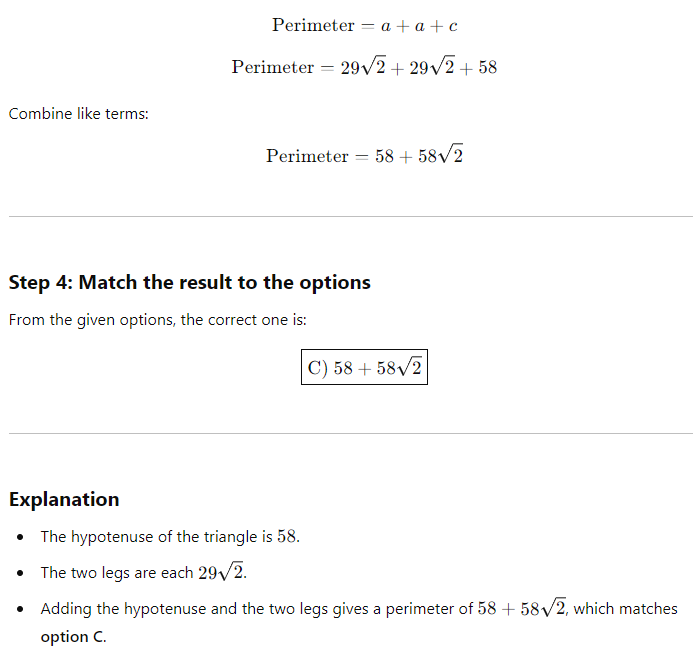
21th Question
Question: In the xy-plane, a parabola has vertex (9, −14) and intersects the x-axis at two points. If the equation of the parabola is written in the form y = ax2 + bx + c, where a, b, and care constants, which of the following could be the value of a + b + c?
A) −23
B) −19
C) −14
D) −12
Choice D:

Choice A is incorrect. If the equation of a parabola with a vertex at (9, -14) is written in the form of the given equation, where a, b, and c are constants and a + b + c = -23, then the value of a will be negative, which means the parabola will open downward, not upward, and will intersect the x-axis at zero points, not two points.
Choice B is incorrect. If the equation of a parabola with a vertex at (9, -14) is written in the form of the given equation, where a, b, and c are constants and a + b + c = -19, then the value of a will be negative, which means the parabola will open downward, not upward, and will intersect the x-axis at zero points, not two points.
Choice C is incorrect. If the equation of a parabola with a vertex at (9, -14) is written in the form of the given equation, where a, b, and c are constants and a + b + c = -14, then the value of a will be 0, which is inconsistent with the equation of a parabola.
Remember the formula, (a – b)2 = Either you can write (a – b) (a – b) or (a2 – 2ab + b2).
Step 1: Understand the problem
We are given:
1. The vertex of the parabola is (9, −14).
~ Therefore, the parabola is expressed in vertex form as:
y = a(x−9)2 − 14
2. The parabola intersects the x-axis, meaning the roots of the parabola exist. This happens when y = 0.
Step 2: General form of a parabola (vertex form)
The vertex form of a parabola is: y = a(x − h)2 + k
where (h, k) is the vertex, and a is a constant that determines the “stretch” or “compression” of the parabola.
Substitute the vertex (9,−14) into the vertex form:
y = a(x − 9)2 − 14
Step 3: Expand the equation to the standard form
Expand y = a(x − 9)2 − 14:
y = a(x2 − 18x + 81) −14
y = ax2 − 18ax + 81a − 14
Thus, the standard form of the equation is:
y = ax2 + (−18a)x + (81a − 14)
Here:
~ a = a,
~ b = -18a,
~ c = 81a – 14.
Step 4: Find the Condition for Intersection
The parabola intersects the x-axis, meaning it has two real roots. This occurs when y = 0. Let’s find the values of x at which y = 0:
0 = a(x − 9)2 − 14
a(x−9)2 = 14
For this equation to have a real solution, a ≠ 0. Therefore, the equation satisfies the condition of having real roots, and a can remain as any non-zero constant.
Step 5: Find the sum a + b + c
The constants a, b, and c are:
~ a = a,
~ b = −18a,
~ c = 81a − 14.
The sum a + b + c is:
a + b + c = a + (-18a) + (81a – 14)
a + b + c = a – 18a + 81a – 14
a + b + c = (1 – 18 + 81)a – 14
a + b + c = 64a − 14
Step 6: Solve for a + b + c When a = −1/4
The problem specifies that the graphs of the equations intersect at exactly one point. This means the quadratic equation has a double root (discriminant = 0). This occurs if we solve for a.

Final Answer
The correct value of a + b + c is: -12.
22th Question

{Note: It is written [0, -99/7], not [0, 99/7].}
A) 5
B) 6
C) 7
D) 8
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A:
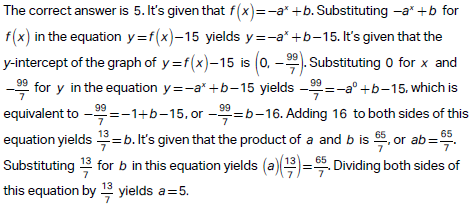
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
To understand it well, keep in mind a few things: When one digit moves from one side to another, it changes its sign from ‘positive to negative’ or ‘negative to positive.’ The second thing is that when a division value moves from one place to another, it goes from ‘up to down’ or ‘down to up’ and then multiplies.
For example: (a) (13/7) = 65/7
65/7 x 7/13
65 x 7 / 7 x 13 OR We can cut 7 of each side then we will have 65/13.
450 / 91 = 5 answer.

Step 2: Combine −1 and −15
Simplify: −1 −15 = −16.
Thus: -99/7 = b – 16.
Step 3: Solve for b
Move −16 to the left-hand side:


Step 5: Verify (Dot ‘.‘ means multiply)
To verify, substitute a = 5 and b = 13/7 back into the condition a . b = 65/7:
a . b = 5 . 13/7
a . b = 65/7.
This confirms the solution is correct.
Did you try all the features and get comfortable using them? You should work on using the calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must try to work on your speed and spend less time on the beginning and more on the later questions. This is the 2nd Practice Test of SAT Math Module 1st.
Either you can take the 3rd Practice Test of SAT Math or the 2nd Practice Test of SAT Math Module 2nd.
- SAT Test 2nd (Math Module 2nd)
- SAT Test 3rd (Math Module 1st)
- SAT Test 2nd (Reading and Writing Module 1st)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


