
Attempt the SATs: Math Test with Real Examination Question, Detailed Explanation Module 1st
Are you also taking the Module 2nd? Because by doing both modules simultaneously will impact your progress better. We have designed a similar exam format with all the necessary features for you to become a master in Math. You just take the SAT Test Module First to practice your skills. The best part is that you practice within the time limit, and there are explanations of the correct answers and tips and tricks to get a perfect score on the SAT. You will find Math easy after this.

ABOUT THE SAT MODULES
The SAT is divided into four modules. There are two categories with each divided into two modules. The first category is “Reading and Writing” with two modules. The second category is “Math” with two modules. The one, you will do below is SAT Math Practice Test Module 1st.
The first module has questions ranging from easy to difficult, but the second module only contains difficult questions. If you want to take some other SATs, visit the links below.
- 1st Module of SAT Reading And Writing Practice Tests
- 2nd Module of SAT Reading And Writing Practice Tests
- 1st Module of SAT Math Practice Tests
- 2nd Module of SAT Math Practice Tests
THE SAT MATH MODULE 1ST
The first module of Math in SAT contains four segments: Algebra, Advanced Math, Problem-Solving and Data Analysis, and Geometry and Trigonometry. The questions in Module 1st are from easy to difficult. In a real SAT exam, you must answer 22 questions within 35 minutes. We have provided you with the same in this Practice Test.
Instructions for the SAT Real-Time Exam
- Go Back-and-Forth: You will see an arrow on the right or left corner of the slide, click to move forward or backward.
- Interaction: You will see a press button at the top right corner that tells you there are some interactive components in the slide. Click the press button to find out.
- Timer: On the top of the slide, you will see the timer, we have divided the time based on the average of the module 1st. (The 35 minutes are equally divided into 22 questions’ time.) It is best to note the time before and after finishing the practice test to measure, “Was it within 35 minutes or not?”
- Mute: You can click on the speaker button to mute the audio.
- Image: You can click on a graph, table, or other image to expand it and view it in full screen.
- Mobile: You cannot take the real exam on mobile, but our practice exam you can give on mobile.
- Calculator: Below the Test, you will see a Desmos calculator and graph for Math. The same, Desmos, will be used in real exams, so learn “How to use Desmos Calculator.”
- Tips: This article will help you learn more about the SAT Exams. SAT: EVERYTHING ABOUT THE SAT
Our team has reviewed some of the best SAT learning materials for your convenience. These materials are best for your career growth.
- SAT Study Cards: https://amzn.to/3NJLI4O
- SAT Math Tricks Baron’s Workbook: https://amzn.to/40Y3klB
- Check Our Review Blog: review.mrenglishkj.com
Wait for the Desmos Calculator to appear.
SAT MATH QUESTION SOLUTIONS WITH EXPLANATION AND TRICKS
Do not open the tabs before finishing the practice test above! For your convenience, we have compiled all the solutions and their explanations here. We will also give you some tips or advice to help you understand them better. You’ll see ‘why this answer is correct’ and ‘why this is incorrect.’
Math Solutions and Explanations:
The light red color shows the Question, green shows the Correct answer, red shows the Incorrect one, and blue shows Tips or Tricks with step-by-step explanations.
1st Question
Question: The total cost, in dollars, to rent a surfboard consists of a $25 service fee and a $10 per hour rental fee. A person rents a surfboard for t hours and intends to spend a maximum of $75 to rent the surfboard. Which inequality represents this situation?
A) 10t ≤ 75
B) 10 + 25t ≤ 75
C) 25t ≤ 75
D) 25 + 10t ≤ 75
Choice D is correct. The cost of the rental fee depends on the number of hours the surfboard is rented. Multiplying t hours by 10 dollars per hour yields a rental fee of 10t dollars. The total cost of the rental consists of the rental fee plus the 25 dollar service fee, which yields a total cost of 25 + 10t dollars. Since the person intends to spend a maximum of 75 dollars to rent the surfboard, the total cost must be at most 75 dollars. Therefore, the inequality 25 + 10t < 75 represents this situation.
Choice A is incorrect. This represents a situation where the rental fee, not the total cost, is at most 75 dollars.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Analysis:
We are tasked with forming an inequality based on the total cost of renting a surfboard, where:
~ A service fee of $25 is charged once.
~ A rental fee of $10 per hour is charged for t hours.
~ The person can spend a maximum of $75.
We need to find the inequality that represents this situation.
Step-by-Step Solution:
1. Break Down the Total Cost:
~ The service fee is $25 (constant, does not depend on hours).
~ The rental fee is $10 per hour, which is represented as 10t, where t is the number of hours.
~ Thus, the total cost is given by:
Total Cost = 25 + 10t
2. Write the Inequality:
~ The person wants to spend no more than $75, meaning the total cost must be less than or equal to $75:
25 + 10t ≤ 75
3. Verify the Answer by Simplifying the Inequality:
~ Start with 25 + 10t ≤ 75.
~ Subtract 25 from both sides to isolate the term involving t: 10t ≤ 75 − 25
~ Simplify: 10t ≤ 50
~ Divide both sides by 10: t ≤ 5
This inequality indicates the person can rent the surfboard for a maximum of 5 hours while staying within the $75 budget.
4. Choose the Correct Option:
~ The correct inequality is: 25 + 10t ≤ 75
~ This matches Option D.
Verification:
~ If t = 5:
Total Cost = 25 + 10(5) = 25 + 50 = 75(Within the budget)
~ If t = 6:
Total Cost = 25 + 10(6) = 25 + 60 = 85(Exceeds the budget)
This confirms the inequality t ≤ 5 holds.
Final Answer: D) 25 + 10t < 75.
2nd Question
Question: The function g is defined by g(x) = x2 + 9. For which value of x is g(x) = 25?
A) 4
B) 5
C) 9
D) 13
Choice A is correct. It’s given that g(x) = x2 + 9. Substituting 25 for g(x) in this equation yields 25 = x2 + 9. Subtracting 9 from both sides of this equation yields 16 = x2. Taking the square root of each side of this equation yields x = ±4. It follows that g(x) = 25 when the value of x is 4 or -4. Only 4 is listed among the choices.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis:
The function g(x) is defined as:
g(x) = x2 + 9
We are asked to find the value(s) of x such that:
g(x) = 25
This means solving the equation:
x2 + 9 = 25
Step-by-Step Solution:
1. Set up the equation: Start with the equation:

The values of x are x = 4 and x = -4. But the option only has 4, not -4.
Final Answer: A) 4.
3rd Question
Question: Each face of a fair 14-sided die is labeled with a number from 1 through 14, with a different number appearing on each face. If the die is rolled one time, what is the probability of rolling a 2?
A) 1/14
B) 2/14
C) 12/14
D) 13/14
Choice A is correct. The total number of possible outcomes for rolling a fair 14-sided die is 14. The number of possible outcomes for rolling a 2 is 1. The probability of rolling a 2 is the number of possible outcomes for rolling a 2 divided by the total number of possible outcomes, or 1/14.
Choice B is incorrect. This is the probability of rolling a number no greater than 2.
Choice C is incorrect. This is the probability of rolling a number greater than 2.
Choice D is incorrect. This is the probability of rolling a number other than 2.
Problem Analysis:
The question asks us to determine the probability of rolling a 2 on a fair 14-sided die, where each face is labeled from 1 through 14, and each outcome is equally likely.

Final Answer: A) 1/14.
4th Question
Question: A printer produces posters at a constant rate of 42 posters per minute. At what rate, in posters per hour, does the printer produce the posters?
A) 2,540
B) 2,520
C) 2,440
D) 2,420
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 2,520. There are 60 minutes in one hour. At a rate of 42 posters per minute, the number of posters produced in one hour can be determined by (42 posters/1 minute)(60 minutes/1 hour), which is 2,520 posters per hour.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis:
The question provides the printing rate as 42 posters per minute and asks to convert this rate into posters per hour.
Step-by-Step Solution:
1. Understand the relationship between minutes and hours:
~ There are 60 minutes in 1 hour.
~ To convert the rate from posters per minute to posters per hour, multiply the rate by the number of minutes in an hour.
2. Calculate the hourly rate:
~ The printer produces 42 posters per minute.
~ Multiply this rate by 60 to find the rate in posters per hour: Posters per hour = 42 × 60
3. Perform the multiplication:
~ Calculate: 42 × 60 = 2,520
4. Interpret the result:
~ The printer produces 2,520 posters per hour.
Final Answer: B) 2,520.
5th Question
Question: The function f is defined by the equation f(x) = 7x + 2. What is the value of f(x) when x = 4?
A) 7
B) 30
C) 13
D) 7.5
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 30. The value of f(x) when x = 4 can be found by substituting 4 for x in the given equation f(x) = 7x + 2. This yields f(4) = 7(4) + 2, or f(4) = 30. Therefore, when x = 4, the value of f(x) is 30.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis:
The function is given as f(x) = 7x + 2. The question asks for the value of f(x) when x = 4. To find this, substitute x = 4 into the function and calculate f(x)
Step-by-Step Solution:
1. Understand the function:
~ The function f(x) = 7x + 2 takes an input x, multiplies it by 7, and then adds 2.
2. Substitute x = 4 into the function:
~ Replace x with 4 in the equation:
f(4) = 7(4) + 2
3. Perform the multiplication:
~ Calculate 7 × 4:
7 × 4 = 28
4. Add 2 to the result:
~ Add 2 to 28:
28 + 2 = 30
Verify the result:
Substituting x = 4 into f(x) = 7x + 2 gives:
f(4) = 30
Final Answer: B) 30.
6th Question
Question: If 4x − 28 = −24, what is the value of x − 7?
A) −24
B) −22
C) −6
D) −1
Choice C:

Choice A is incorrect. This is the value of 4x – 28, not x – 7.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Analysis:
The given equation is 4x − 28 = −24, and we are tasked to find the value of x − 7. First, solve for x using the given equation, then substitute that value to compute x − 7.
Step-by-Step Solution:
1. Solve for x in the given equation:
~ Start with the equation: 4x − 28 = −24
~ Add 28 to both sides to isolate the 4x term:
4x = −24 + 28
~ Simplify the right-hand side:
4x = 4
~ Divide both sides by 4 to solve for x:
x = 1
2. Find the value of x − 7:
~ Substitute x = 1 into x − 7:
x − 7 = 1 − 7
~ Simplify the result:
x − 7 = −6
Verify the solution:
~ Substitute x = 1 into the original equation 4x − 28 = −24:
4(1) − 28 = −24
4 − 28 = −24
-24 = −24
The solution x = 1 is correct.
Final Answer: The value of x − 7 is: C) −6.
7th Question
Question: For a snowstorm in a certain town, the minimum rate of snowfall recorded was 0.6 inches per hour, and the maximum rate of snowfall recorded was 1.8 inches per hour. Which inequality is true for all values of s, where s represents a rate of snowfall, in inches per hour, recorded for this snowstorm?
A) s ≥ 2.4
B) s ≥ 1.8
C) 0 ≤ s ≤ 0.6
D) 0.6 ≤ s ≤ 1.8
Choice D is correct. It’s given that for a snowstorm in a certain town, the minimum rate of snowfall recorded was 0.6 inches per hour, the maximum rate of snowfall recorded was 1.8 inches per hour, and s represents a rate of snowfall, in inches per hour, recorded for this snowstorm. It follows that the inequality 0.6 < s < 1.8 is true for all values of s.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
We are asked to determine the inequality that represents all possible values of s, the rate of snowfall (in inches per hour), during a snowstorm where the minimum recorded snowfall rate is 0.6 inches per hour, and the maximum recorded snowfall rate is 1.8 inches per hour.
Step-by-Step Solution:
1. Understand the range of s:
~ The minimum snowfall rate is 0.6 inches per hour, so s must be greater than or equal to 0.6.
~ The maximum snowfall rate is 1.8 inches per hour, so s must be less than or equal to 1.8.
2. Combine the two conditions:
Both conditions can be combined into a single inequality:
0.6 ≤ s ≤ 1.8
~ This inequality states that s, the snowfall rate, is always between 0.6 and 1.8 inches per hour, inclusive of these values.
3. Verify the solution:
~ Any value of s within this range satisfies the minimum and maximum rates of snowfall.
~ For example:
~ If s = 0.6, it satisfies the condition s ≥ 0.6.
~ If s = 1.8, it satisfies the condition s ≤ 1.8.
~ If s = 1.0, it satisfies 0.6 ≤ 1.0 ≤ 1.80.
Thus, the inequality 0.6 ≤ s ≤ 1.8 is correct.
Final Answer: The inequality is:
0.6 ≤ s ≤ 1.8
8th Question
y = 4x
y = x2 − 12
Question: A solution to the given system of equations is (x, y), where x > 0. What is the value of x?
A) 6
B) 12
C) 4
D) 5
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is correct. The correct answer is 6. It’s given that y = 4x and y = x2 – 12. Since y = 4x, substituting 4x for y in the second equation of the given system yields 4x = x2 – 12. Subtracting 4x from both sides of this equation yields 0 = x2 – 4x – 12. This equation can be rewritten as 0 = (x – 6)(x + 2). By the zero product property, x – 6 = 0 or x + 2 = 0. Adding 6 to both sides of the equation x – 6 = 0 yields x = 6. Subtracting 2 from both sides of the equation x + 2 = 0 yields x = -2. Therefore, solutions to the given system of equations occur when x = 6 and when x = -2. It’s given that a solution to the given system of equations is (x, y), where x > 0. Since 6 is greater than 0, it follows that the value of x is 6.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
There are two ways to do this equation.
1. Quadratic Formula
2. Factoring Formula
1. Quadratic Formula:
Problem Breakdown:
We are solving a system of equations with the following two equations:
y = 4x (linear equation)
y = x2 − 12 (quadratic equation)
The goal is to find the x-value of the solution where x > 0.
Step-by-Step Solution:
1. Substitute y = 4x into y = x2 − 12:
Since both equations represent y, we can set them equal to each other:
4x = x2 − 12
2. Rearrange into standard quadratic form:

4. Select the valid solution:
The problem specifies x > 0. Therefore, the valid solution is:
x = 6
5. Verify the solution:
~ Substitute x = 6 into y = 4x:
y = 4(6)
y = 24
~ Check that (6, 24) satisfies y = x2 − 12:
y = 62 − 12
y = 36 − 12
y = 24
Both equations are satisfied, so x = 6 is correct.
Final Answer: A) 6.
2. Factoring Formula:
Step-by-Step Solution:
1. Substitute y = 4x into y = x2 − 12:
Since both equations represent y, we equate them:
4x = x2 − 12
2. Rearrange into standard quadratic form:
Move all terms to one side of the equation:
x2 − 4x − 12 = 0
3. Factor the quadratic equation:
We factor x2 − 4x − 12 into two binomials:
x2 − 4x − 12 = (x − 6)(x + 2)
4. Solve for x:
Set each factor equal to 0:
x − 6 = 0 ⇒ x = 6
x + 2 = 0 ⇒ x = −2
5. Select the valid solution:
The problem specifies x > 0, so the valid solution is:
x = 6
6. Verify the solution:
~ Substitute x = 6 into y = 4x:
y = 4(6) = 24
~ Check that (6, 24) satisfies y = x2 − 12:
y = 62 − 12
y = 36 − 12
y = 24
Both equations are satisfied, so x = 6 is the correct and it is greater than 0, x > 0.
Final Answer: A) 6.
9th Question
Question: A store sells two different-sized containers of blueberries. The store’s sales of these blueberries totaled 896.86 dollars last month. The equation 4.51x + 6.07y = 896.86 represents this situation, where x is the number of smaller containers sold and y is the number of larger containers sold. According to the equation, what is the price, in dollars, of each smaller container?
A) 6.07
B) 4.51
C) 896.86
D) 10.58
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 4.51. It’s given that the equation 4.51x + 6.07y = 896.86 represents this situation, where x is the number of smaller containers sold, y is the number of larger containers sold, and 896.86 is the store’s total sales, in dollars, of blueberries last month. Therefore, 4.51x represents the store’s sales, in dollars, of smaller containers, and 6.07y represents the store’s sales, in dollars, of larger containers. Since x is the number of smaller containers sold, the price, in dollars, of each smaller container is 4.51.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Restatement:
The equation given is:
4.51x + 6.07y = 896.8
where:
x = the number of smaller containers sold.
y = the number of larger containers sold.
We are tasked with determining the price of each smaller container.
Step-by-Step Solution:
1. Identify the coefficients:
In the equation 4.51x + 6.07y = 896.86:
~ 4.51 is the coefficient of x, the number of smaller containers sold.
~ This coefficient represents the price of each smaller container in dollars.
Thus:
Price of each smaller container = 4.51 dollars.
2. Verify the Interpretation:
The equation models the total sales as the sum of:
~ 4.51x: the revenue from selling smaller containers at $4.51 each, and
~ 6.07y: the revenue from selling larger containers at $6.07 each.
The units of 4.51 are dollars per smaller container, confirming that 4.51 is indeed the price of each smaller container.
Final Answer: The price of each smaller container is = 4.51 dollars.
10th Question
Question: A right circular cylinder has a base diameter of 22 centimeters and a height of 6 centimeters. What is the volume, in cubic centimeters, of the cylinder?
A) 132π
B) 264π
C) 726π
D) 2,904π
Choice C is correct. The volume, V, of a right circular cylinder is given by the formula V = πr2h, where r is the radius of the base of the cylinder and h is the height of the cylinder. It’s given that a right circular cylinder has a height of 6 centimeters. Therefore, h = 6. It’s also given that the cylinder has a base diameter of 22 centimeters. The radius of a circle is half the diameter of the circle. Since the base of a right circular cylinder is a circle, it follows that the radius of the base of the right circular cylinder is 22/2, or 11, centimeters. Therefore, r = 11. Substituting 11 for r and 6 for h in the formula V = πr2h yields V = (11)2(6), which is equivalent to V = π(121)(6), or V = 726π. Therefore, the volume, in cubic centimeters, of the cylinder is 726π.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Restatement:
We are tasked with finding the volume of a right circular cylinder with:
~ Base diameter = 22 cm
~ Height = 6 cm.
Step-by-Step Solution:
1. Recall the formula for the volume of a cylinder:
The volume V of a cylinder is given by:
V = πr2h
where:
r = radius of the base,
h = height of the cylinder,
π = pie is a constant (~3.14159).
2. Calculate the radius r:
The diameter of the base is 22 cm. The radius is half the diameter:
r = diameter/2
r = 22/2
r = 11 cm.
3. Substitute values into the formula:
Using r = 11 cm and h = 6 cm:
V = π(11)2(6).
4. Simplify the expression:
First, calculate 112:
112 = 121.
Then multiply by the height:
121 × 6 = 726.
Thus: V = 726π cubic centimeters.
Final Answer: The volume of the cylinder is: 726π cm3.
11th Question
Question: Square P has a side length of x inches. Square Q has a perimeter that is 176 inches greater than the perimeter of square P. The function f gives the area of square Q, in square inches. Which of the following defines f?
A) f(x) = (x + 44)2
B) f(x) = (x + 176)2
C) f(x) = (176x + 44)2
D) f(x) = (176x + 176)2
Choice A is correct. Let x represent the side length, in inches, of square P. It follows that the perimeter of square P is 4x inches. It’s given that square Q has a perimeter that is 176 inches greater than the perimeter of square P. Thus, the perimeter of square Q is 176 inches greater than 4x inches, or 4x +176 inches. Since the perimeter of a square is 4 times the side length of the square, each side length of Q is 4x + 176 divided by 4, or x + 44 inches. Since the area of a square is calculated by multiplying the length of two sides, the area of square Q is (x + 44)(x + 44), or (x + 44)2 square inches. It follows that function f is defined by f(x) = (x + 44)2.
Choice B is incorrect. This function represents a square with side lengths (x + 176) inches.
Choice C is incorrect. This function represents a square with side lengths (176x + 44) inches.
Choice D is incorrect. This function represents a square with side lengths (176x + 176) inches.
Problem Breakdown and Step-by-Step Solution:
We are tasked with finding a function f(x) that defines the area of Square Q, based on the relationship between the perimeters of Squares P and Q.
1. Understanding the Relationship Between the Squares:
Square P:
~ Side length of Square P: x inches.
~ Perimeter of Square P: 4x (since the perimeter of a square is 4× side length).
Square Q:
~ Its perimeter is 176 inches greater than the perimeter of Square P.
~ Perimeter of Square Q: 4x + 176.

5. Verifying the Answer:
~ x represents the side length of Square P.
~ Adding 176 to Square P’s perimeter results in Square Q’s perimeter.
~ Dividing Square Q’s perimeter by 4 gives its side length, x + 44.
~ Squaring x + 44 gives the area of Square Q.
Thus, our logic and calculations confirm the correctness of Option A.
Final Answer: A) f(x) = (x + 44)2.
12th Question
Question:

Choice C:

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
We need to solve for w in terms of x and y.
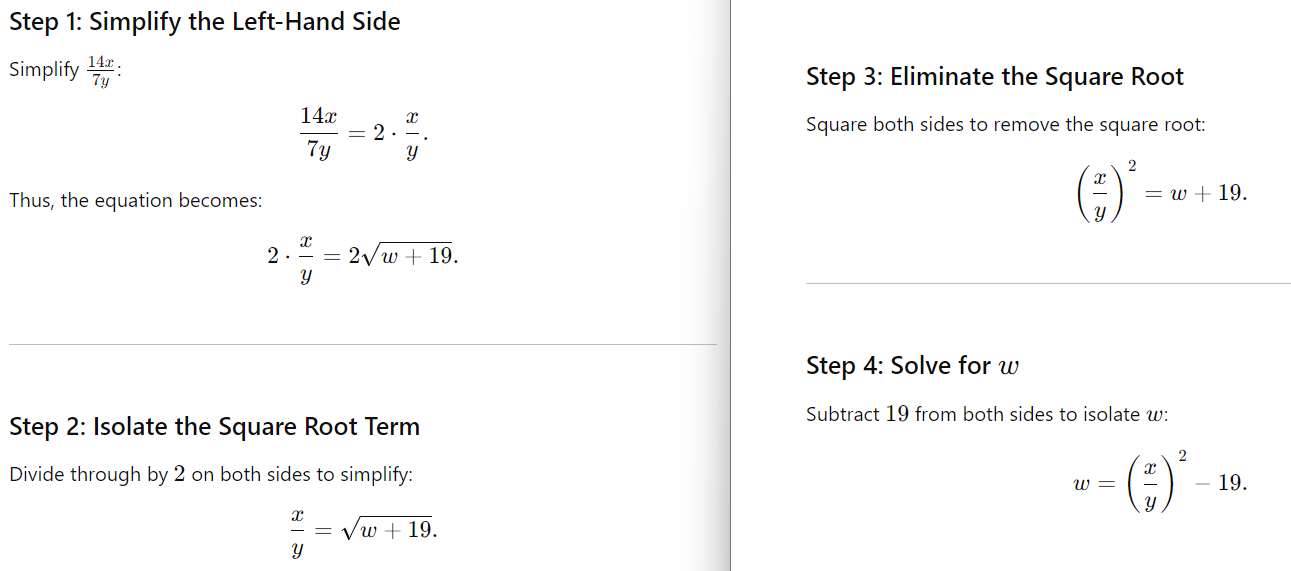
Step-by-Step Explanation:
Step 1: On the left side, 7 divides 14 and we get 2.
Step 2: Notice, that we have cut 2 from both sides. We can cut the same thing from both sides if we do it to both sides.
Step 3: You can either solve a root or use the square root method. It is called a Square Root because ‘root’s inverse is square’ and ‘square inverse is a root,’ so we can put a square on both sides and on the right side; a square cuts the root. Hence, we get w + 19.
Step 4: When we move from one side to another, the sign changes from positive to negative. Here, we only move +19 to the left side and it becomes -19.
Final Answer: Option C.
13th Question
Question: Point O is the center of a circle. The measure of arc RS on this circle is 100°. What is the measure, in degrees, of its associated angle ROS?
A) 90
B) 100
C) 120
D) 180
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice B is correct. The correct answer is 100. It’s given that point O is the center of a circle and the measure of arc RS on the circle is 100o. It follows that points R and S lie on the circle. Therefore, mean OR and mean OS are radii of the circle. A central angle is an angle formed by two radii of a circle, with its vertex at the center of the circle. Therefore, ∠ROS is a central angle. Because the degree measure of an arc is equal to the measure of its associated central angle, it follows that the measure, in degrees, of ∠ROS is 100.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Explanation:
We are given a circle centered at O, where the measure of arc RS is 100∘. We are tasked to find the measure of the central angle ∠ROS associated with this arc.
Key Concept:
~ A central angle in a circle is an angle whose vertex is at the center of the circle, and its sides intersect the circle, creating an intercepted arc.
~ The measure of the central angle is equal to the measure of the intercepted arc in degrees.
Step-by-Step Solution:
~ The arc measure of RS is given as 100∘.
~ Since ∠ROS is a central angle, its measure is exactly equal to the measure of the intercepted arc RS.
~ Therefore, ∠ROS = 100∘.
Verification:
The definition of a central angle confirms that the angle’s measure equals the arc’s measure. Thus, there is no further calculation needed.
Final Answer: The measure of ∠ROS is 100°.
14th Question
Question:
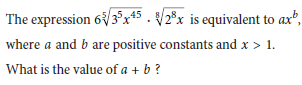
A) 88.635
B) 73.836
C) 36.738
D) 45.125
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice D is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
The question asks for this the expression is equal to axb where a and b are positive constants. It is clear that the value of a and b is going to be positive. What is the value of a + b. Now, the question asked us to find the individual values of a and b then add them a + b.
Why axb ≠ a + b (General Rule)
~ The form axb means multiplication of a and xb.
~ You only add a and b if the question explicitly asks for their sum, as it does here.
If the question did not specify to calculate a + b, then the expression axb would remain as it is.

After getting 36. We move to 2nd part of Step 3:
2. Combine the powers of x using the rule xm ⋅ xn = xm + n:
x9 ⋅ x1/8 = x9 + 1/8.
15th Question
Question:
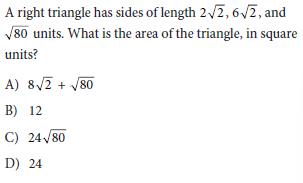
Choice B is correct.

Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
The problem involves a right triangle with three sides and tasks to find the area of this triangle.

Final Answer: B) 12.
16th Question
(x − 3)2 + (y + 7)2 = 64
Question: The graph of the given equation is a circle in the xy-plane. The point (p, q) lies on the circle. Which of the following is the smallest possible value for p?
A) 5
B) -5
C) -11
D) 11
Choice B is correct.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation: (x + 3)2 + (y + 7)2 = 64
Understanding the Given Equation of a Circle
The standard form of a circle’s equation is:
(x − h)2 + (y − k)2 = r2,
where:
~ (h, k) is the center of the circle,
~ r is the radius of the circle.
Step 1: Identify the Center and Radius
From the given equation:
(x − 3)2 + (y + 7)2 = 64.
The center of the circle is (3, −7).
The radius is r = root of 64 is = 8.
Step 2: What Does “Point Lies on the Circle” Mean?
If a point (p, q) lies on the circle, then its coordinates satisfy the circle’s equation. That is:
(p − 3)2 + (q + 7)2 = 64.
We are tasked with finding a possible value for p. Since there are infinitely many points on the circle, we can assume specific conditions to simplify the problem.
Step 3: Assume y = −7 (Horizontal Line Through the Center)
If we assume y = −7, the point lies on the horizontal line through the center of the circle. Substituting y = −7 into the circle’s equation:
(x − 3)2 + (−7 + 7)2 = 64.
Simplify the equation:
(x − 3)2 + 0 = 64.
Thus:
(x − 3)2 = 64.
Step 4: Solve for x
Take the square root of both sides:
x − 3 = square root of 64.
Simplify:
x − 3 = ±8.
Solve for x in both cases:
1) x − 3 = 8 ⟹ x = 11 – 3 ⟹ x = 11,
2) x − 3 = −8 ⟹ x = −8 + 3 ⟹ x = −5.
The question asks for the smallest possible value of p, which is -5 here.
Final Answer: B) -5.
17th Question
I. f(x) = −5(4)x − 7
II. g(x) = −2(3)x + 4
Question: Which of the following functions has a minimum value at x = −2?
A) I only
B) II only
C) I and II
D) Neither I nor II
Choice D is the correct answer.
Choice A is incorrect and may result from conceptual or calculation errors.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Step-by-Step Explanation:
Understanding the Problem
We need to determine whether the given exponential functions f(x) and g(x) have a minimum value at a specific x-coordinate (x = −2).
~ Exponential functions generally take the form:
y = a ⋅ bx + c
where:
a determines the direction of the graph:
~ If a > 0, the function increases.
~ If a < 0, the function decreases.
b is the base of the exponential (it must be positive).
c is a vertical shift, which affects the horizontal asymptote of the graph.
For a function to have a minimum value, we look at whether the graph is decreasing and approaches a horizontal asymptote.
Step 1: Analyze f(x) = −5(4)x −7
~ The coefficient of the exponential term is −5, which is negative.
~ ~ A negative coefficient means the graph is decreasing as x increases.
~ The base of the exponential is 4 > 0, which is valid.
~ The term −7 is a vertical shift. This tells us the graph has a horizontal asymptote at y = −7.
In this case:
~ Since the graph decreases and approaches −7 as x → ∞, there is no minimum point because the graph never “turns around.”
~ Instead, the function continuously decreases and gets close to the asymptote.
Thus, f(x) does not have a minimum at x = −2.
Step 2: Analyze g(x) = −2(3)x + 4
~ The coefficient of the exponential term is −2, which is also negative.
~ ~ A negative coefficient again indicates the graph is decreasing as x increases.
~ The base of the exponential is 3 > 0, which is valid.
~ The term +4 is a vertical shift. This tells us the graph has a horizontal asymptote at y = 4.
In this case:
~ The graph decreases and approaches y = 4 as x → ∞, and like before, there is no minimum point.
~ The function continuously decreases but never achieves a minimum because the graph approaches the asymptote asymptotically.
Thus, g(x) does not have a minimum at x = −2.
Step 3: Conclusion
Neither function f(x) nor g(x) has a minimum value at x = −2.
Final Answer: D) Neither I nor II.
18th Question
Question: A sample of oak has a density of 807 kilograms per cubic meter. The sample is in the shape of a cube, where each edge has a length of 0.90 meters. To the nearest whole number, what is the mass, in kilograms, of this sample?
A) 588
B) 726
C) 897
D) 1,107
Choice A is correct. It’s given that the sample is in the shape of a cube with edge lengths of 0.9 meters. Therefore, the volume of the sample is 0.903, or 0.729, cubic meters. It’s also given that the sample has a density of 807 kilograms per 1 cubic meter. Therefore, the mass of this sample is 0.729 cubic meters (807 kilograms/1 cubic meter), or 588.303 kilograms. Rounding this mass to the nearest whole number gives 588 kilograms. Therefore, to the nearest whole number, the mass, in kilograms, of this sample is 588.
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Problem Breakdown:
We are tasked with finding the mass of an oak sample given the following information:
1. Density of the oak: 807 kg/m3
2. The sample is a cube with each of the edges length: 0.90 m.
The formula to calculate the mass is:
Mass = Density × Volume
Here:
~ Density = 807 kg/m3
~ Volume = Side length3
Step 1: Find the Volume of the Cube
The volume of a cube is calculated as:
Volume = Side length3
Substitute the side length of 0.90 m:
Volume = (0.90)3
Calculate:
(0.90)3 = 0.90 × 0.90 × 0.90 = 0.729 m3
Thus, the volume of the cube is:
Volume = 0.729 m3
Step 2: Calculate the Mass
The formula for mass is:
Mass = Density × Volume
Substitute the given density (807 kg/m3) and the calculated volume (0.729 m3):
Mass = 807 × 0.729
Perform the multiplication:
807 × 0.729 = 588.303
To the nearest whole number:
Mass ≈ 588 kg
Final Answer: The mass of the oak sample is 589 kilograms.
19th Question
Question: For x > 0, the function f is defined as follows: f(x) equals 201% of x
Which of the following could describe this function?
A) Decreasing exponential
B) Decreasing linear
C) Increasing exponential
D) Increasing linear
Choice D is correct. It’s given that for x > 0, f(x) is equal to 201% of x. This is equivalent to f(x) = 201/100 . x, or f(x) = 2.01x, for x > 0. This function indicates that as x increases, f(x) also increases, which means f is an increasing function. Furthermore, f(x) increases at a constant rate of 2.01 for each increase of x by 1. A function with a constant rate of change is linear. Thus, the function f can be described as an increasing linear function.
Choice A is incorrect and may result from conceptual errors.
Choice B is incorrect and may result from conceptual errors.
Choice C is incorrect. This could describe the function f(x) = (2.01)x, where f(x) is equal to 201% of f(x – 1), not x, for x > 0.
Step 1: Interpret “201% of x“
When a value is described as a percentage of x:
201% of x = 201 ÷ 100 × x = 2.01x
Thus, the function f(x) is:
f(x) = 2.01x
This is a linear function because the equation is of the form f(x) = mx+b, where:
~ m = 2.01 (the slope), and
~ b = 0 (no constant term).
Since the slope m = 2.01 > 0, the function is increasing.
Step 2: Analyze the Options
1. Option A: Decreasing exponential
A decreasing exponential function has the form f(x) = a ⋅ bx, where 0 < b < 1 (the base is less than 1).
~ This does not match f(x) = 2.01x, which is linear.
2. Option B: Decreasing linear
~ A decreasing linear function has a negative slope, i.e., m < 0.
~ Here, the slope m = 2.01 is positive, so the function is increasing, not decreasing.
3. Option C: Increasing exponential
~ An increasing exponential function has the form f(x) = a ⋅ bx, where b > 1 (the base is greater than 1).
~ This function is not exponential because there is no exponent on x in f(x) = 2.01x.
4. Option D: Increasing linear
~ An increasing linear function has a positive slope m > 0.
~ Since f(x) = 2.01x has a positive slope of 2.01, this option is correct.
Step 3: Verify the Correct Answer
The function f(x) = 2.01x:
~ Is linear because it is of the form mx + b, where m = 2.01 > 0.
~ Is increasing because the slope mmm is positive.
Thus, the correct answer is: D) Increasing linear
20th Question
Question:
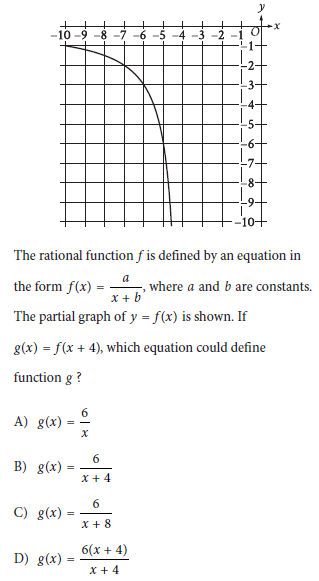
Choice C is the correct one.
Choice A is incorrect. This could define function g if g(x) = f(x – 4).
Choice B is incorrect. This could define function g if g(x) = f(x).
Choice D is incorrect. This could define function g if g(x) – f(x) . (x + 4).
Problem Breakdown:
We have the equation f(x) = a/x + b with no values given. Our job is to look up the graph to find some values.
The question shows that y = f(x), which means y = a/x + b.
After studying the graph, we find three points:
x = −7, y = −2,
x = −6, y = −3,
x = −5, y = −6.
We need to define function g. But first, we need to put the x and y values into the function to get constants a and b.
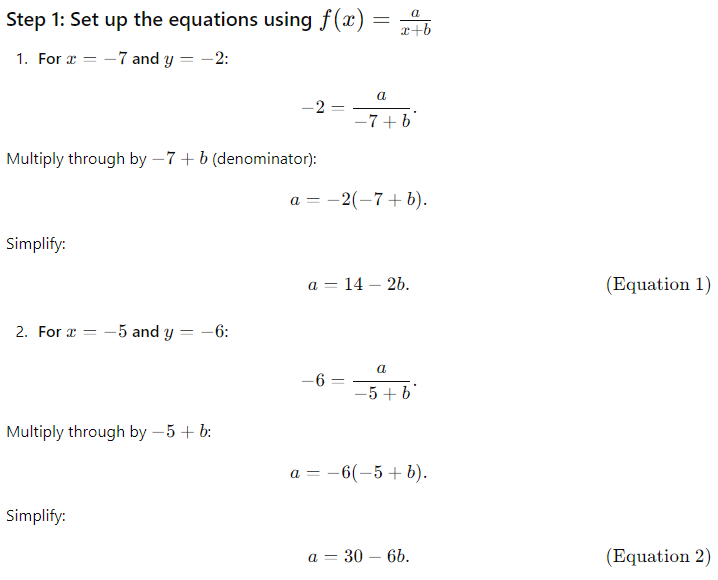
Step 2: Solve for b using Equation 1 and Equation 2
From the two expressions for a:
14 − 2b = 30 − 6b.
Simplify the equation:
14 + 4b = 30.
Subtract 14 from both sides:
4b = 16.
Divide by 4: b = 4.
Step 3: Solve for a using b = 4
Substitute b = 4 into either Equation 1 or Equation 2. Using Equation 1:
a = 14− 2b.
Substitute b = 4:
a = 14 − 2(4).
Simplify:
a = 14 − 8 = 6.
Thus, a = 6 and b = 4.
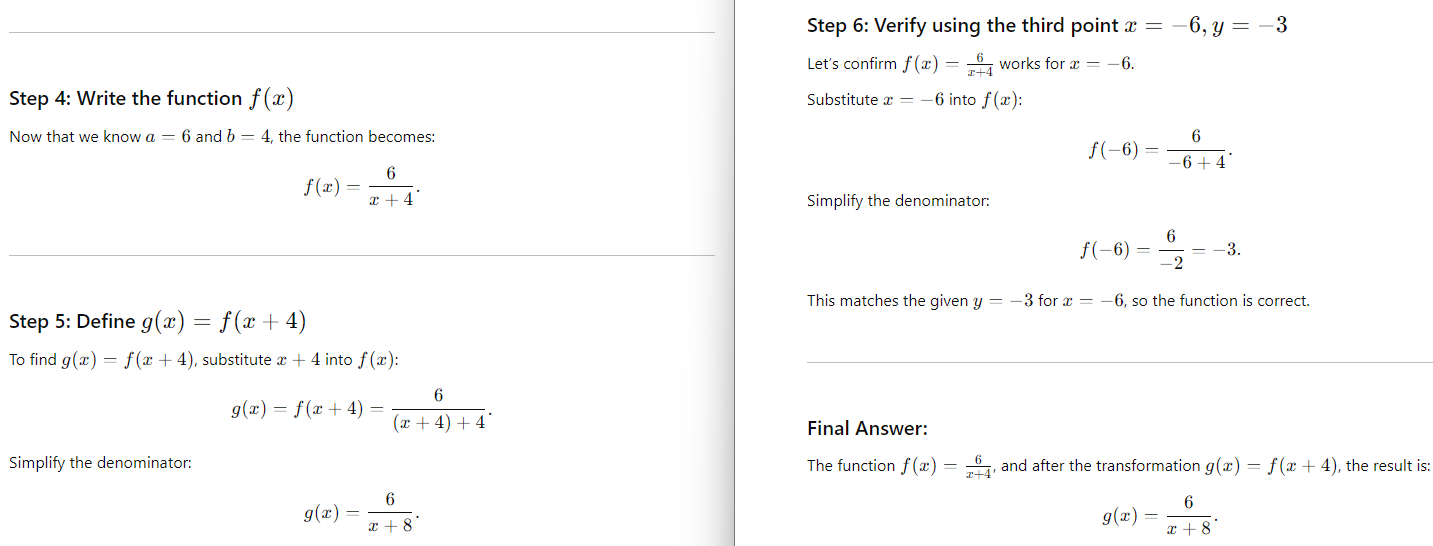
Final Answer: Option C.
21th Question
| Angle Cruz | 483 |
| Terry Smith | 320 |
Question: The table shows the results of a poll. A total of 803 voters selected at random were asked which candidate they would vote for in the upcoming election. According to the poll, if 6,424 people vote in the election, by how many votes would Angel Cruz be expected to win?
A) 163
B) 1,304
C) 3,864
D) 5,621
Choice B is correct. It’s given that 483 out of 803 voters responded that they would vote for Angel Cruz. Therefore, the proportion of voters from the poll who responded they would vote for Angel Cruz is 483/803. It’s also given that there are a total of 6,424 voters in the election. Therefore, the total number of people who would be expected to vote for Angel Cruz is 6,424(483/803), or 3,864. Since 3,864 of the 6,424 total voters would be expected to vote for Angel Cruz, it follows that 6,424 – 3,864, or 2,560 voters would be expected not to vote for Angel Cruz. The difference in the number of votes for and against Angel Cruz is 3,864 – 2,560, or 1,304 votes. Therefore, if 6,424 people vote in the election, Angel Cruz would be expected to win by 1,304 votes.
Choice A is incorrect. This is the difference in the number of voters from the poll who responded that they would vote for and against Angel Cruz.
Choice C is incorrect. This is the total number of people who would be expected to vote for Angel Cruz.
Choice D is incorrect. This is the difference between the total number of people who vote in the election and the number of voters from the poll.
Step 1: Understand the Problem and Define the Formula
The problem involves scaling up poll results to predict actual election outcomes.
The general formula to estimate votes based on proportions is:

Step 3: Use the Formula to Estimate Votes in the Election
We now use the formula:
Estimated Votes = Proportion × Total Voters.
Here, the Total Voters in the election = 6,424.
1. Estimated Votes for Angel Cruz:
Cruz’s Votes = 0.6015 × 6,424.
Perform the calculation:
0.6015 × 6,424 = 3,864 votes.
2. Estimated Votes for Terry Smith:
Smith’s Votes = 0.3985 × 6,424.
Perform the calculation: 0.3985 × 6,424 = 2,560 votes.
Step 4: Calculate the Margin of Victory
The margin of victory is the difference between Angel Cruz’s and Terry Smith’s votes:
Margin = Votes for Cruz − Votes for Smith.
Substitute the values:
Margin = 3,864 − 2,560.
Simplify:
Margin = 1,304 votes.
Final Answer: Angel Cruz is expected to win by 1,304 votes.
22th Question
Question: The graph of x2 + x + y2 + y = 199/2 in the xy-plane is a circle. What is the length of the circle’s radius?
A) 10
B) 100
C) 1,000
D) 10,000
[Type-Based Answer: In the final exam, you will type the answer rather than choose from options.]
Choice A is the correct answer.
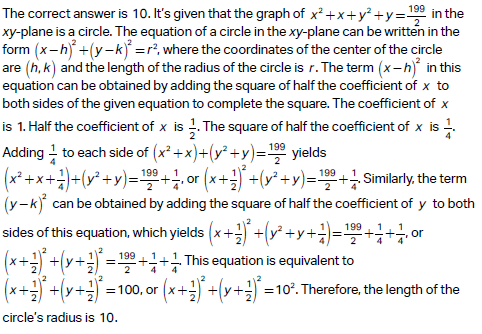
Choice B is incorrect and may result from conceptual or calculation errors.
Choice C is incorrect and may result from conceptual or calculation errors.
Choice D is incorrect and may result from conceptual or calculation errors.
Step 1: Understand the General Equation of a Circle
The general form of a circle’s equation is:
(x − h)2 + (y − k)2 = r2
Where:
~ (h, k) is the center of the circle.
~ r is the radius of the circle.
If the equation we’re given is not already in this form, we need to complete the square for the x-terms and y-terms to rewrite it in standard form.
Step 2: Given Equation
The equation is:
x2 + x + y2 + y = 199/2.
Our goal is to complete the square for the x-terms and y-terms.
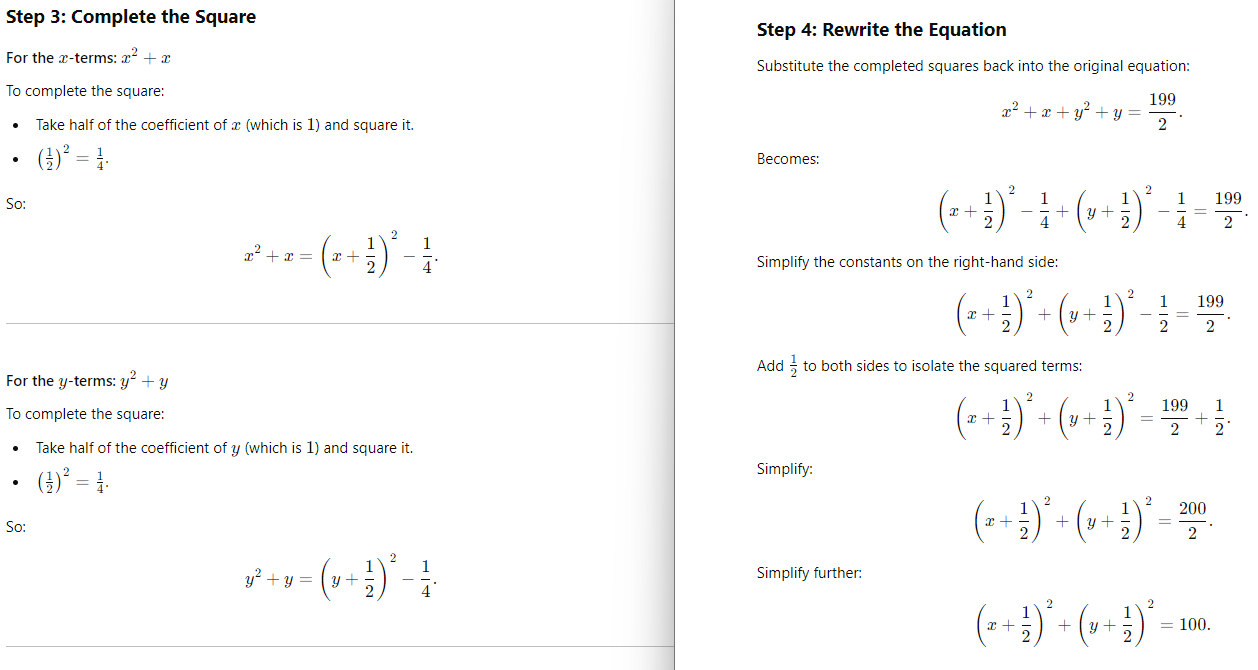
Step 5: Identify the Radius
From the standard form of a circle:
(x − h)2 + (y − k)2 = r2,
we see that r2 = 100.
To find r, take the square root of both sides:
r = square root of 100
r = 10.
Final Answer: The radius of the circle is 10.
Did you try all the features and get comfortable using them? You should work on using the calculator and seeing references and directions. So be prepared for everything before taking the final SAT exam. The explanation of answers makes it easy to learn and progress. You must try to work on your speed and spend less time on the beginning and more on the later questions. This is the 7th Practice Test of SAT Math Module 1st.
Either you can take the 8th Practice Test of SAT Math or the 7th Practice Test of SAT Math Module 2nd.
- SAT Test 7th (Math Module 2nd)
- SAT Test 8th (Math Module 1st)
- SAT Test 7th (Reading and Writing Module 1st)
The best way to become a master in Math is to find the correct answer and understand why other options are incorrect. I wish you luck in your bright career.


